北师大版九年级下册数学随堂小练：2确定二次函数的表达式 6页

数学随堂小练北师大版（2012）九年级下册 2.3 确定二次函数的表达式 一、单选题 1.已知二次函数的图象如图所示，则这个二次函数的表达式为( ) A. 2 2 3y x x   B. 2 2 3y x x   C. 2 2 3y x x   D. 2 2 3y x x   2.已知二次函数 2 4y ax x c   ,当 2x   时,函数值是-1;当 1x  时.函数值是 5,则此二次函数的 表达式为( ) A. 22 4 1y x x   B. 2 4 2y x x   C. 22 4 1y x x    D. 22 4 1y x x   3.如图所示的一条抛物线,则其解析式为( ) A. 2 2 3y x x   B. 2 2 3y x x   C. 2 2 3y x x   D. 2 2 3y x x   4.已知抛物线的顶点坐标是 (2,1) ,且抛物线经过点 (3,0) ,则这条抛物线的解析式是( ) A. 2 4 3y x x    B. 2 4 3y x x    C. 2 4 3y x x   D. 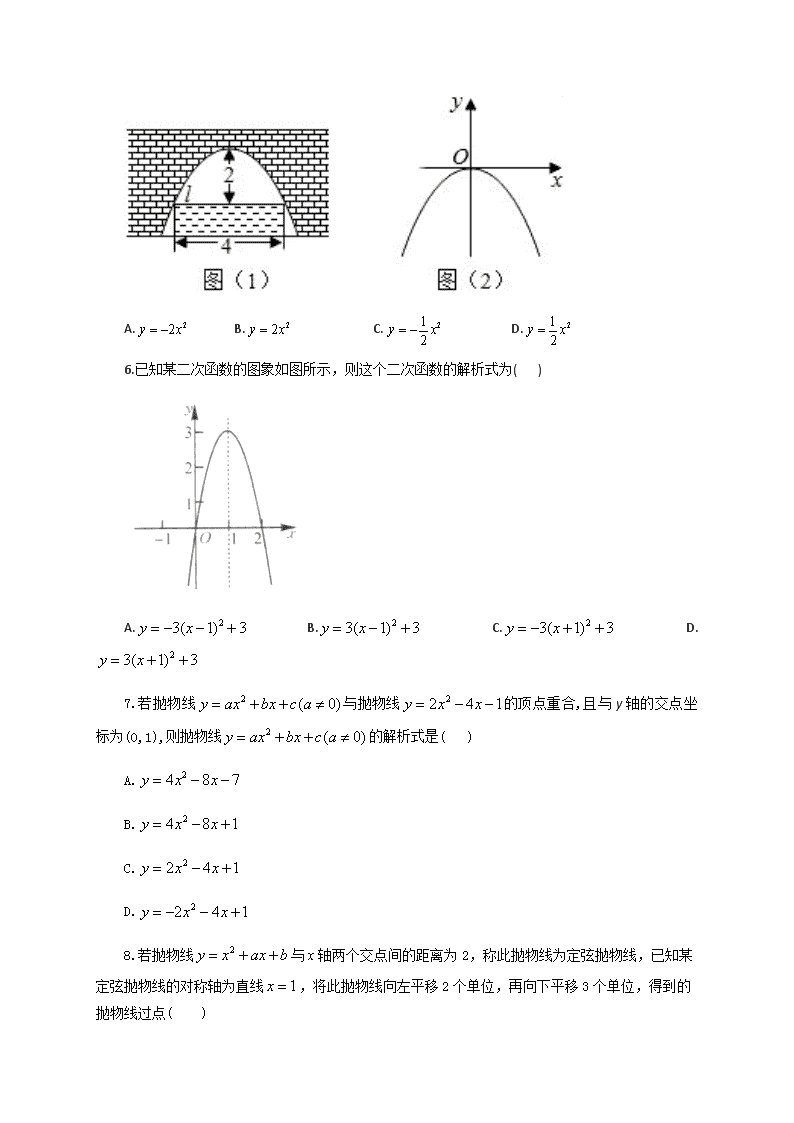2 4 3y x x    5.图⑴是一个横断面为抛物线形状的拱桥,当水面在 1 时,拱顶(拱桥洞的最高点)离水面 2m,水面 宽 4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( ) A. 22y x  B. 22y x C. 21 2y x  D. 21 2y x 6.已知某二次函数的图象如图所示，则这个二次函数的解析式为( ) A. 23( 1) 3y x    B. 23( 1) 3y x   C. 23( 1) 3y x    D. 23( 1) 3y x   7.若抛物线 2 ( 0)y ax bx c a    与抛物线 22 4 1y x x   的顶点重合,且与 y 轴的交点坐 标为(0,1),则抛物线 2 ( 0)y ax bx c a    的解析式是( ) A. 24 8 7y x x   B. 24 8 1y x x   C. 22 4 1y x x   D. 22 4 1y x x    8.若抛物线 2y x ax b   与 x 轴两个交点间的距离为 2，称此抛物线为定弦抛物线，已知某 定弦抛物线的对称轴为直线 1x  ，将此抛物线向左平移 2 个单位，再向下平移 3 个单位，得到的 抛物线过点( ) A. ( 3, 6)  B. ( 3,0) C.( 3, 5)  D. ( 3, 1)  9.已知二次函数的部分图象如图所示,对称轴是直线 1x   ,则这个二次函数的表达式为（ ） A. 2 2 3y x x    B. 2 2 3y x x   C. 2 2 3y x x    D. 2 2 3y x x    二、填空题 10.某抛物线型拱桥如图所示，当拱顶离水面 2m 时，水面宽 4m，水面下降 2m，水面宽度增 加 .m. 11.已知二次函数的图象经过点 ( 1,0) ， (3 0)， 和 (0 3)， ，求该二次函数的解析式. 12.在平面直角坐标系 xOy 中，若抛物线 2y ax bx c   的顶点为 M，且经过  0,4A ，  4,4B 两点，若 M 到线段 AB 的距离为 4,则 a  . 13.已知二次函数的图象过点 ( 3 2) ， ，且它的顶点坐标为 ( 2 3) ， ，则此二次函数的解析式 为 . 三、解答题 14.已知:二次函数 2y x bx c    的图象过点 ( 1, 8),(0, 3)   . 1.求此二次函数的表达式,并用配方法将其化为 2( )y a x h k   的形式 2.画出此函数图象的示意图 参考答案 1.答案：B 解：根据题意，图象与 轴交于负半轴，故 c 为负数，又四个选项中，B C、 的 c 为 3 ，符合题 意，故 设二次函数的表达式为 2y a bx c   ， 抛物线过    1,0 0, 3 3,0  ， 所以 0 3 9 3 0 a b c c a b c           ， 解得 1, 2, 3a b c     这个二次函数的表达式为 2 2 3y x x   ． 故选 B． 2.答案：A 根据题意得 4 8 1, 4 5, a c a c         解得 2, 1 a c     所以二次函数的表达式为 22 4 1y x x   . 3.答案：B 因为抛物线与 x 轴的交点坐标为 ( 1,0),(3,0) ， 所以可设为交点式 ( 1)( 3)( 0)y a x x a    ， 把 (0, 3) )代入 ( 1)( 3)y a x x   , 可得 3 (0 1) (0 3)a     ，解得 1a  . 所以解析式为 2( 1)( 3) 2 3y x x x x      4.答案：D 设抛物线的解析式为 2( 2) 1( 0)y a x a    ，把 (3,0) 代入得 2(3 2) 1 0a    .解得 1a   ，所以 抛物线的解析式为 2 2( 2) 1 4 3y x x x        .故选 D. 5.答案：C 抛物线顶点为 (0,0) ，所以设抛物线方程为 2 ( 0)y ax a  (2, 2) 是图像上的点，所以 22 2a   , 1 2a   故选 C 6.答案：A 由图象得， 0a  ，顶点坐标为 (1,3) A 项符合题意，故选 A. 7.答案：B 22 4 1y x x   22( 1) 3x   ，抛物线 22 4 1y x x   的顶点坐标为 (1, 3) .抛物线 2y ax bx c   与抛物线 22 4 1y x x   的顶点重合， 抛物线 2y ax bx c   的顶点坐标为 (1, 3) ，设此抛物线为 2( 1) 3y a x   .与 y 轴的交点坐标为 (0,1) ， 1 3a   ，解得 4a  ， 此抛物线为 24( 1) 3y x   24 8 1x x   .故选 B. 8.答案：B ∵某定弦抛物线的对称轴为直线 1x  ， ∴该定弦抛物线过点 (0,0) (2,0)、 ， ∴该抛物线解析式为 2 2( 2) 2 ( 1) 1y x x x x x       ． 将此抛物线向左平移 2 个单位，再向下平移 3 个单位，得到新抛物线的解析式为 2 2( 1 2) 1 3 ( 1) 4y x x        ． 当 3x   时， 2( 1) 4 0y x    ， ∴得到的新抛物线过点 ( 3,0) ． 故选：B． 9.答案：D 由题图知二次函数图象过点 ( 3,0) (0,3) 、 ,∵对称轴为直线 1x   ,∴设二次函数表达式为 2( 1)y a x k   ，将 ( 3,0) (0,3) 、 代入，得 4 0, 3, a k a k      解得 1, 4, a k     ∴二次函数的表达式为 2 2( 1) 4 2 3y x x x        。 10.答案： 4 2 4 以 AB 为 x 轴， AB 的垂直平分线为 y 轴建立如图所示的平面直角坐标系 依题意可得 2 0 2 0( ) ( ) ( )0 2A B C ，， ，， ， ， 设经过 A B C， ， 三点的抛物线的解析式为   2 2y a x x   ， 2( )0CQ ， 在此抛物线上， 1 2a   此抛物线的解析式为   1 2 22y x x    Q 水面下降 2m，   1 2 2 22 x x     ， 解得 1 22 2 2 2x x  ， ， 下降之后的水面宽为 42m ∴水面宽度增加了 4 2 4 m 11.答案：解:设二次函数的解析式为 2 ( )0y ax bx c a    ，把 ( )1 )0 3 0( ，，， 和 (0 )3， 代入 2 ( )0y ax bx c a    ， 得 0 9 3 0 3 a b c a b c c           ，解得 1 2 3 a b c        二次函数的解析式为 2 2 3y x x   . 12.答案： 1a  或-1 解析:  0,4A ，  4,4B , //AB x 轴. 点 M 到线段 AB 的距离为 4,. (2,8)M 或 (2,0) . ①当 (2,8)M 时，设抛物线的解析式为 2( 2) 8y a x   ，将点  0,4A 代入得， 4 8 4a   ,解得 1a   ;②当 (2,0)M 时，设抛物线的解析式为 2( 2)y a x  ，将点  0,4A 代入得， 4 4a  ，解 得 1a  ，所以 1a  或-1. 13.答案： 2 4 1y x x   设二次函数的解析式为  22 3 0( )y a x a    ，把点 ( 3 2) ， 代入得  23 2 3 2a     g ， 解得 1a  ，所以二次函数的解析式为  2 22 3 4 1y x x x      14.答案：1.二次函数的表达式为 2 24 3 1( ); 2y x x y x        2.∵ 22( ) 1y x    , ∴顶点坐标为 (2,1) ,对称轴方程为 2x  . ∵函数二次函数 2 4 3y x x    的开口向下,顶点坐标为 (2,1) ,与 x 轴的交点为 (3,0),(1,0) ,