九年级上册数学周周测第二十四章 圆周周测2（24-1） 人教版 6页

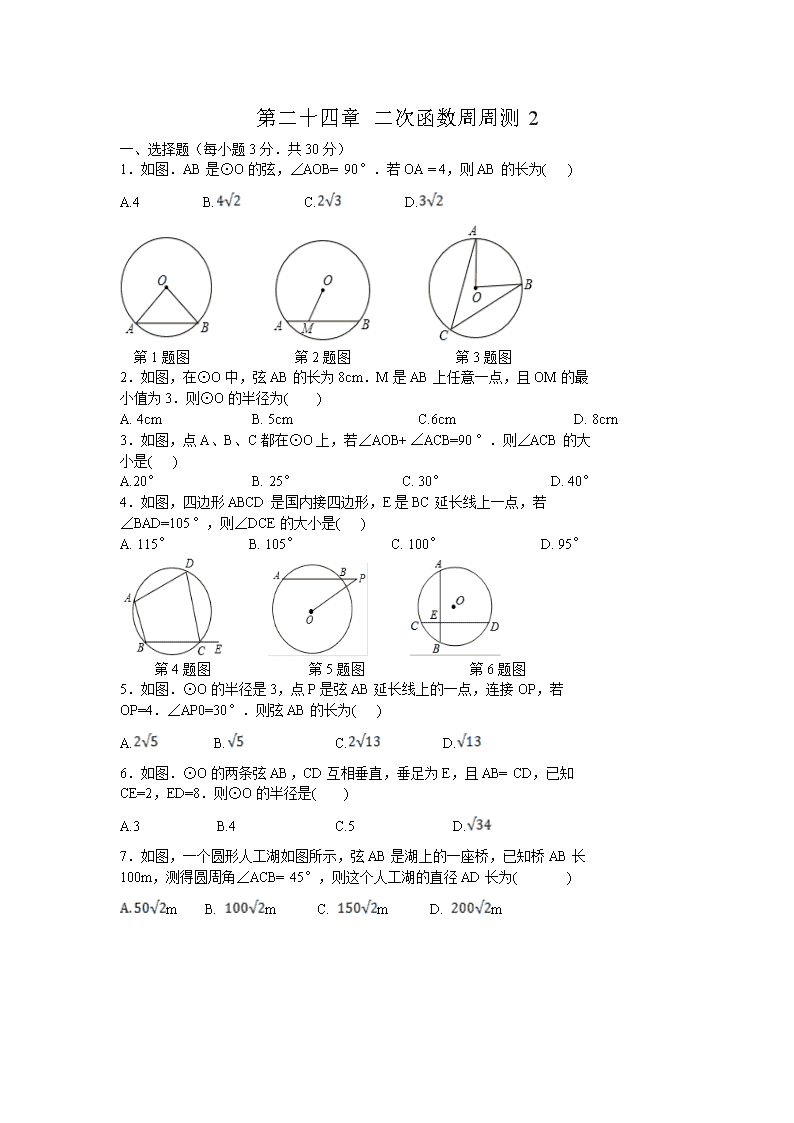
第二十四章 二次函数周周测 2 一、选择题（每小题 3 分．共 30 分） 1．如图．AB 是⊙O 的弦，∠AOB= 90°．若 OA = 4，则 AB 的长为( ) A.4 B. C. D. 第 1 题图 第 2 题图 第 3 题图 2．如图，在⊙O 中，弦 AB 的长为 8cm．M 是 AB 上任意一点，且 OM 的最 小值为 3．则⊙O 的半径为( ) A. 4cm B. 5cm C.6cm D. 8crn 3．如图，点 A、B、C 都在⊙O 上，若∠AOB+∠ACB=90°．则∠ACB 的大 小是( ) A.20° B. 25° C. 30° D. 40° 4．如图，四边形 ABCD 是国内接四边形，E 是 BC 延长线上一点，若 ∠BAD=105°，则∠DCE 的大小是( ) A. 115° B. 105° C. 100° D. 95° 第 4 题图 第 5 题图 第 6 题图 5．如图．⊙O 的半径是 3，点 P 是弦 AB 延长线上的一点，连接 OP，若 OP=4．∠AP0=30°．则弦 AB 的长为( ) A. B. C. D. 6．如图．⊙O 的两条弦 AB，CD 互相垂直，垂足为 E，且 AB= CD，已知 CE=2，ED=8．则⊙O 的半径是( ) A.3 B.4 C.5 D. 7．如图，一个圆形人工湖如图所示，弦 AB 是湖上的一座桥，已知桥 AB 长 100m，测得圆周角∠ACB= 45°，则这个人工湖的直径 AD 长为( ) m B. m C. m D. m 第 7 题图 第 8 题图 第 9 题图 8．如同．AB 是⊙O 的直径，AB=10，弦 AC=8，O⊥AC 于 E，交⊙O 于 D，许诺 BE，则 BE 的长为( ) A. B. C.5 D.6 9-如图，以△ABC 的边 BC 为直径的⊙O 分别交 AB，AC 于 D,E，若 ∠DOE=60°,AD=~ ,则 AC 的长为( ) A. B. 2 C. D. 10.如图，△ABC 中，∠BAC=90°.AB=AC=2．D 为 AC 上—动点，以 AD 为直径的⊙O 变 BD 于 E．则线段 CE 的最小值为( ) A． B． C． D． 二、填空题（每小题 3 分，共 18 分） 11.⊙O 上一点 C,且∠BOC=44°，则∠A 的度数为 ． 第 11 题图 第 12 题图 第 13 题图 12．如图．AB、AC 都是圆 O 的弦，OM⊥AB．ON⊥AC．垂足分别为 M、 N，如果 MN =3．那么 BC= ． 13．如图．AB 是⊙O 的直径，点 D 在⊙O 上，∠AOD=130°，BC∥OD 交 ⊙O 于 C．则∠A 的度数是 ． 14．如图所示，在⊙O 中，已知∠BAC=∠CDA=25°。则∠ABO 的度数为 . 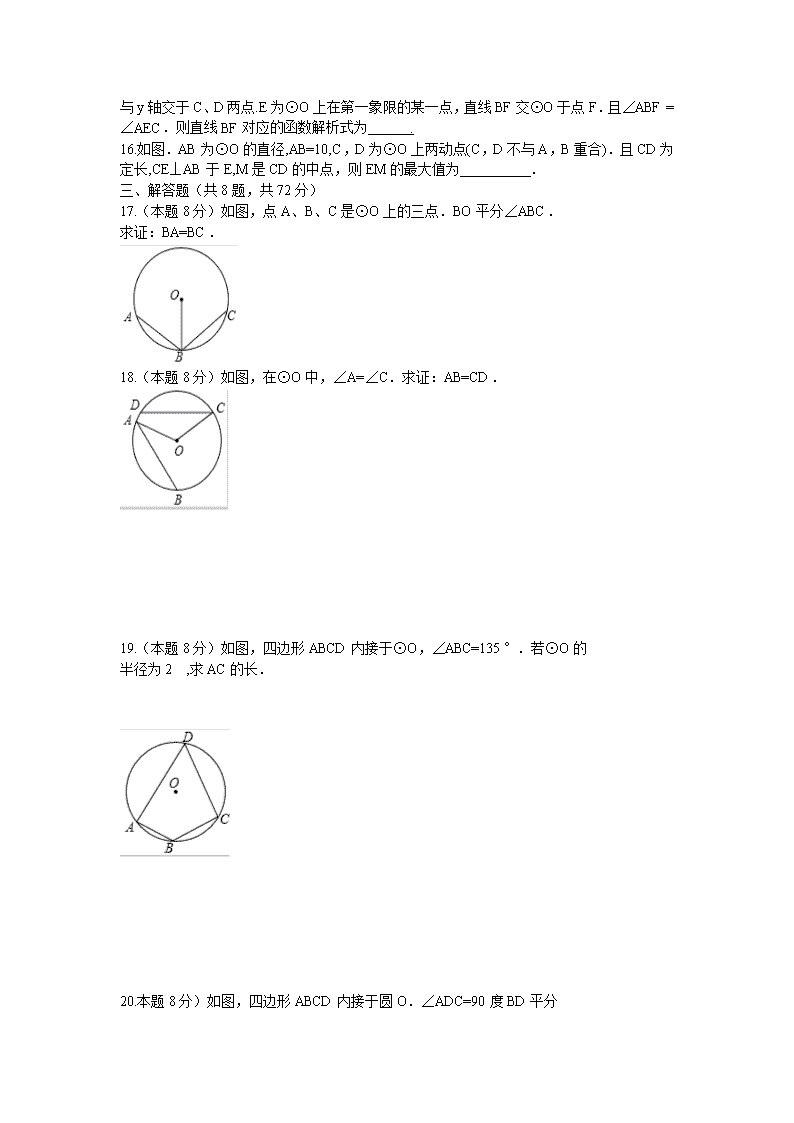第 14 题图 第 15 题图 第 16 题图 15.如图，在直角坐标系中，以坐标原点为圆心、半径为 1 的⊙O 与 x 轴交于 A、B 两点， 与 y 轴交于 C、D 两点.E 为⊙O 上在第一象限的某一点，直线 BF 交⊙O 于点 F．且∠ABF = ∠AEC．则直线 BF 对应的函数解析式为 . 16.如图．AB 为⊙O 的直径,AB=10,C，D 为⊙O 上两动点(C，D 不与 A，B 重合)．且 CD 为 定长,CE⊥AB 于 E,M 是 CD 的中点，则 EM 的最大值为 ． 三、解答题（共 8 题，共 72 分） 17.（本题 8 分）如图，点 A、B、C 是⊙O 上的三点．BO 平分∠ABC． 求证：BA=BC． 18.（本题 8 分）如图，在⊙O 中，∠A=∠C．求证：AB=CD． 19.（本题 8 分）如图，四边形 ABCD 内接于⊙O，∠ABC=135°．若⊙O 的 半径为 2 ,求 AC 的长． 20.本题 8 分）如图，四边形 ABCD 内接于圆 O．∠ADC=90 度 BD 平分 ∠A DC,AD=20 ,CD=15．求四边形 ABCD 的面积． 21.（本题 8 分）如图，在单位长度为 1 的正方形网格中，一段圆弧经过格点 A、B、C．以 点 O 为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系． (1)直接写出点 B、C 的坐标：B______、C______； (2)在图中标出该圆弧所在圆的圆心 D 的位置． (3)直接写出⊙D 的半径= （结果保留根号）． 22.（本题 10 分）如图，AD 为⊙O 的直径，CD 为弦， AB = BC ，连接 0B． （1）求证：OB∥CD； （2）若 AB=15，CD=7．求⊙O 的半径． 23.（本题 10 分）已知：△ABC 中，AB=AC，以 AC 为 直径的⊙O 交 BC 于点 D，交 AB 于点 E. (1)如图 1．求证： CD = DE (2)如图 2．若 AB=13，BC=10，F 为半圆的中点，求 DF 的长． 图 1 图 2 24.（本题 l2 分）在平面直角坐标系中 P 点在 x 轴 上，⊙P 交 x 轴于 A、B 两点，交 y 轴于 C.D 两点，E 为⊙O 上一点． 连接 CE. (1)如图①，若 AC = CM ,AB=13，BM=5．求点 C 的坐标； （2）如图②，当 O 为 AP 扣点时，探究 DE,CE,BE 之问的数量关系； （3）如图③，当 0 为 AP 中点时，写出 DE,CE,AE 之问的数量关系 （不证 明）。