中考数学专题复习练习：内角和 15页

典型例题一 例01．在中，‎ ‎（1），则_____________；‎ ‎（2），则_____________；‎ ‎（3），，则_____________. ‎ 分析：三角形的三个内角的和等于，所以，本题有一个隐含的条件，即，所以（1）中，只需把，与，代入上式即可求出. （2）中，我们把已知的式子变形，由. 求得，再代入，得，把与都代入中，即可求得. （3）也可使用. 求，但是因为其中一角是，即三角形为直角三角形，所以也可使用三角形内角和定理的推论1—直角三角形的两个锐角互余来求解. ‎ 解答：（1） （2） （3）‎ 例02．一个三角形的一个外角是它相邻内角的倍，是不相邻内角的3倍，求这个三角形的各内角. ‎ 分析：三角形的一个外角与它相邻的内角之间的关系是互补，而且是与它不相邻内角的和. ‎ 解答：设与这个外角相邻的内角为，‎ 则有 解得 ‎ ‎∴ 这个三角形的三个内角为，，. ‎ 例03．如图，已知：在中，，延长EF与BC的延长线交于G. ‎ 求证：‎ 分析：欲证，只需证. 观察图形，由是的外角得知，又由是的外角可得整理可证明命题. ‎ 证明：∵ （三角形的一个外角等于和它不相邻的两个内有的和）‎ 又∵ （已知），‎ ‎（对顶角相等）‎ ‎∴. ∴ ①‎ 又∵ ②（三角形的一个外角等于和它不相邻的两个内角的和）‎ ‎①＋②得 ∴ ‎ 例04．如图，已知，，. ‎ 求：的大小. ‎ 分析：在中，已知与的大小，可求得的度数，是的一个外角. 有，并且已知与的大小. 可求得的大小. ‎ 解答：∵（三角形内角和定理） ‎ ‎∴‎ ‎∵ （三角形的一个外角等于和它不相邻的两个内角和）. ‎ ‎∴. ‎ 例05．已知：BD为的角平分线，CD为的外角的的平分线，它与BD的延长线交于D. 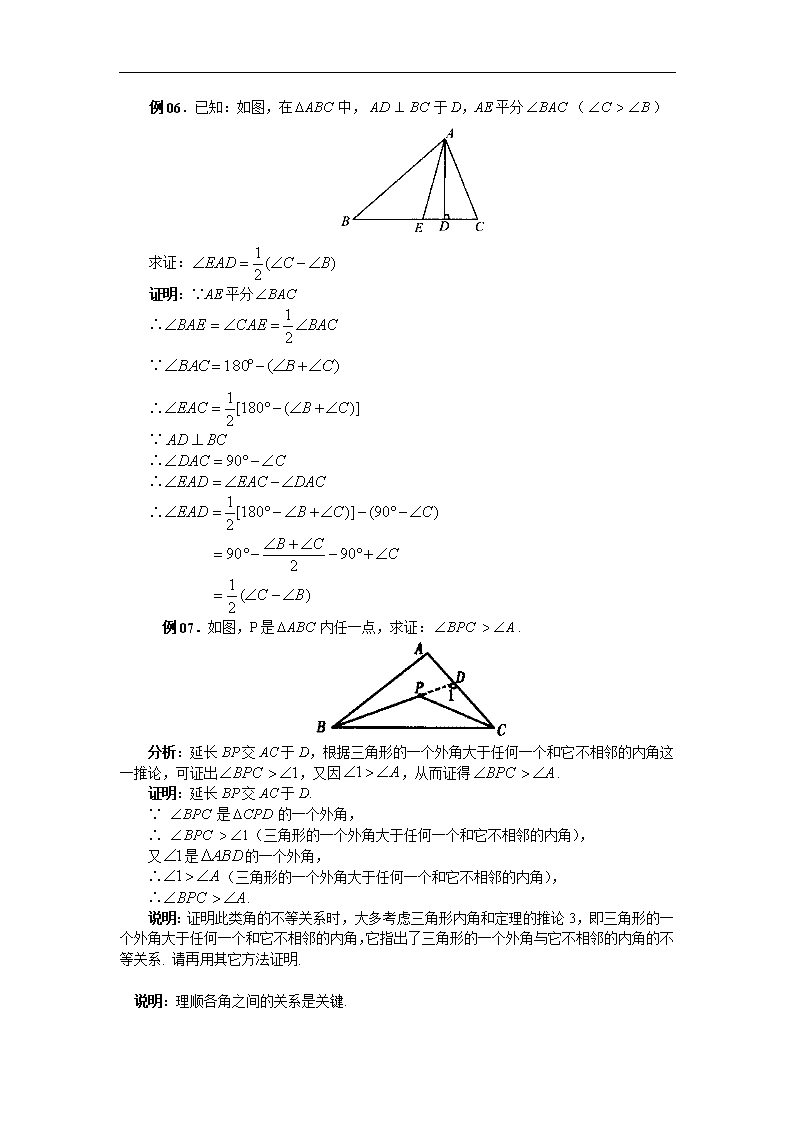（如下图）‎ 求证：‎ 分析：已知三角形的一个内角平分线和一个外角平分线，可以想到利用外角与内角的关系证题，从而有 ‎∴‎ 证明：∵BD、CD分别为、的平分线 ‎∴‎ ‎∵‎ ‎∴‎ 又∵‎ ‎∴‎ 例06．已知：如图，在中，于D，AE平分（）‎ 求证：‎ 证明：∵AE平分 ‎∴‎ ‎∵‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎ ‎ ‎ ‎ ‎ 例07．如图，P是内任一点，求证：. ‎ 分析：延长BP交AC于D，根据三角形的一个外角大于任何一个和它不相邻的内角这一推论，可证出，又因，从而证得. ‎ 证明：延长BP交AC于D. ‎ ‎∵ 是的一个外角，‎ ‎∴ （三角形的一个外角大于任何一个和它不相邻的内角），‎ 又是的一个外角，‎ ‎∴（三角形的一个外角大于任何一个和它不相邻的内角），‎ ‎∴. ‎ 说明：证明此类角的不等关系时，大多考虑三角形内角和定理的推论3，即三角形的一个外角大于任何一个和它不相邻的内角，它指出了三角形的一个外角与它不相邻的内角的不等关系. 请再用其它方法证明. ‎ ‎ 说明：理顺各角之间的关系是关键.‎ 例08．如图，已知，BE平分，CE平分，求证：为直角三角形. ‎ 分析：要证为直角三角形，即证，利用两平行线同旁内角互补和两平行线的内错角相等，以及角平分线定义，不难求出.‎ 证明：略 例09．已知：如图，在中，，BD、CE分别是边AC、AB上的高，BD、CE相交于H，求的度数. ‎ 解答：设 则 ‎∴‎ ‎∴‎ ‎∴ ‎ ‎∵ ∴ ‎ ‎∵ ∴‎ 在中，‎ 说明 用方程思想解答几何求值问题是几何解题中经常使用的.‎ 例10．如图，已知：CE为外角的平分线. CE交AB的延长线于点E. ‎ 求证：‎ 分析：证明角的不等关系，想到本节推论，想到大角是不是某个三角形外角，由图形可知：是的外角，有，而，故只须证，而是的一个外角，是的一个和不相邻的内角，所以，有，故. ‎ 证明：∵CE平分（已知） ∴ ∵ ∴ ∵‎ ‎ ∴‎ 例11．如图，五角星ABCDE，求的度数. ‎ 分析：欲求的度数，则可设法把它们转化为三角形的内角，连结BE，则因为与的内角和都为，且其中的一对内角，∴，即求就是求即求三角形ABE的内角和. ‎ 解答：连结BE，在中，（三角形内角和定理）‎ 即 ‎ 又 ∵ ‎ ‎（三角形内角和定理）‎ ‎（对顶角相等）‎ ‎∴ ‎ ‎∴ ‎ 填空题 ‎（1）在中，‎ ‎①若，，那么________.‎ ‎②如果，那么_________，______.‎ ‎③如果，那么______.‎ ‎④，那么_________，______，________.‎ ‎⑤如果，，那么______，______，________.‎ ‎（2）如图，，，分别是的三个外角，那么______.‎ ‎（3）如图，已知，，，则______.‎ ‎（4）如果三角形的三个角都相等，那么每个内角都等于______.‎ ‎（5）CD是斜边AB上的高，，则________，_______，______.‎ ‎（6）如图，于D，AE平分，，，则_______；‎ ‎（7）如图，________；‎ ‎（8）一个三角形的两角分别为和，则第三个角的平分线与它对边上的高的夹角等于_______；‎ ‎（9）如图，，，，则________.‎ ‎（10）如图，在直角三角形ABC中，，，的平分线相交于O点，则_______；‎ 参考答案：‎ ‎（1）① ②， ③‎ 提示： 两式相加，可得，∴‎ ‎④，， ⑤，，‎ ‎（2） （3） （4） （5），， ‎ ‎（6） ‎ 提示：‎ ‎，‎ ‎∴‎ ‎（7）提示： ‎ ‎（8） （9） （10） ‎ 填空题 ‎（1）如图，已知，，，则_______.‎ ‎（2）如图，________.‎ ‎（3）如图，已知的和的外角夹发线交于D，，则_______.‎ ‎（4）如图，在中，已知AD平分交BC于D，，，那么_______.‎ ‎（5）如图，，，，则______.‎ ‎（6）如图，的一个外角，，则_______.‎ 参考答案：‎ ‎（1） ‎ ‎（2）提示：四边形外角之和为，所以的邻补角为，∴ ‎ ‎ （3），提示，与相邻外角度数为，所以和的外角的一半为，∴ ‎ ‎（4） ‎ ‎（5），提示：连结CD，则 ‎（6）‎ 解答题 ‎1．计算题 ‎（1）如图，已知，，，求，的度数.‎ ‎（2）如图，已知AD是的角平分线，，，求各内角的度数.‎ ‎（3）如图，已知，，.求的大小.‎ ‎（4）如图，已知中，，，，求的大小.‎ ‎（5）如图，已知，，，求的大小.‎ ‎（6）如图，已知于D，于E.，.求的大小.‎ ‎（7）如图，已知，，，求的度数.‎ ‎（8）如图，的一个内角平分线与一个外角平分线交于点D，，，求的度数.‎ 参考答案：‎ ‎1．计算题 ‎（1）解：（已知）‎ ‎∴（两直线平行，同位角相等）‎ ‎ 又∵（三角形内角和定理）‎ ‎ ‎ ‎（2）解：∵（已知）‎ ‎（三角形的一个外角等于和它不相邻的两个内的和）‎ ‎∴ ‎ AD为的角平分线.‎ ‎∴‎ ‎（三角形内角和定理）‎ ‎∴‎ ‎（3）解：（已知）‎ ‎∴（直角三角形两个锐角互余）‎ ‎∴‎ ‎∴（对顶角相等）‎ ‎∵（三角形的一个外角等于和它不相邻的两个内角的和）‎ ‎∴‎ ‎（4）解：.（三角形的一个外角等于和它不相邻的两个内角的和）‎ ‎∵ （已知）‎ ‎∴‎ 又∵（直角三角形两个锐角互余）‎ ‎∴ ‎ ‎∵（三角形内角和定理）‎ ‎∴‎ ‎（5）解：（三角形内角和定理）‎ ‎ ∴ （三角形的一个外角等于和它不相邻的两个内角的和）‎ ‎∴‎ ‎（6）解：（三角形的一个外角等于和它不相邻的两个内角的和）‎ ‎ 其中，，（已知）‎ ‎∴ ∴ ‎ ‎ （直角三角形两个锐角互余）‎ ‎ ‎ ‎ ∴ ‎ ‎（7）解：（已知）‎ ‎∴，（两直线平行，同位角相等）‎ ‎（两直线平行，同旁内角互补）‎ ‎∴‎ ‎ （三角形的一个外角等于和它不相邻的两个内角的和）‎ 又∵ （已知）‎ ‎∴ ‎ ‎∴‎ ‎∴‎ ‎∵（三角形内角和定理）‎ ‎∴‎ ‎（8）解：（三角形内角和定理）‎ ‎∴‎ ‎（三角形一个外角等于和它不相邻的两个内角的和）‎ ‎∴ ‎ ‎（三角形内角和定理）‎ ‎∴ ‎ 解答题 ‎1．证明题 ‎（1）如图，已知中，，，D，E为垂足，BD和CE交于点H.求证：.‎ ‎（2）如图，D、E分别在AB、AC上，已知，.求证：.‎ ‎（3）如图，已知D是BC上的一点，且.求证：.‎ ‎（4）如图，已知.求证：.‎ ‎（5）如图，已知：BCD，CAE，AFB为直线，求证：.‎ ‎（6）如图，已知D是的外角平分线与BA的延长线的交点.求证：.‎ ‎（7）如图，已知：在中，的平分线与的平分线相交于点I.‎ 求证：.‎ ‎（8）如图，已知：的三个内角平分线AD，BI，CI相交于点I，于点H.求证：.‎ 参考答案：‎ ‎1．证明题 ‎（1）证明：（已知）‎ ‎∴ （垂直定义）‎ ‎∴，（直角三角形的两个锐角互余）‎ ‎∴（同角的余角相等）‎ ‎（2）证明：∵，（三角形内角和定理）‎ 又∵ （已知）‎ ‎∴ ‎ ‎∴ ‎ ‎∴ （同位角相等，两直线平行）‎ ‎（3）证明：∵（已知）‎ ‎∴‎ 又∵（三角形的一个外角等于和它不相邻的两个内角的和）‎ ‎∴‎ ‎（4）证明：∵（三角形的一个外角等于和它不相邻的两个内角的和）‎ 又 ∵ ‎ ‎∴ ‎ ‎∴（内错角相等，两直线平行）‎ ‎（5）证明：∵（三角形的一个外角大于任何一个和它不相邻的内角）‎ ‎∴ ‎ ‎（6）证明：∵ （三角形的一个外角等于和它不相邻的两个内角的和）‎ ‎ 又 ∵ （外角平分线定义）‎ ‎∴ ‎ ‎∴ ‎ ‎（7）证明：应用三角形内角和定理得 ‎ ‎ ‎（8）证明：∵ （直角三角形的两个锐角互余），‎ 即 ‎ ‎ ‎ ‎1、判断题：‎ A、三角形的外角大于它的内角.‎ B、三角形的一个外角等于它的两个内角.‎ C、三角形的外角和是180度.‎ D、三角形的外角中一定有一个锐角.‎ E、若一个三角形有一个外角是100度，则此三角形为锐角三角形.‎ ‎2、下列命题中真命题是（　　）.‎ A、一个钝角三角形一定不是等腰三角形 B、钝角三角形是斜三角形　　‎ C、等腰三角形是斜三角形　　　　‎ D、任意三角形是斜三角形 ‎3、三角形一个内角平分线与其相应的外角平分线位置关系是（　　）.‎ ‎　　A、相交 　　B、垂直 C、互为反向延长线 　D、不能确定 ‎4、三角形的一个外角小于和它相邻的内角，则这个三角形是（　　）.‎ ‎　　A、锐角三角形　　B、直角三角形　　C、钝角三角形　D、都有可能 ‎5、三角形中最大角的范围为＿＿＿，最小角的范围为＿＿＿＿.‎ ‎6、‎ ‎ 7、‎ ‎8、五角星的五个角的度数之和是＿＿＿＿每一个角的度数是＿＿＿＿.‎ ‎9、‎ 答案: 1.A 错; B 错;C 错;D 错;E错.‎ ‎ 2.B; 3. B; 4. C ; 5. 　大角：　小角：; 6. 180度; 7. 70度. 8. 180度. 9. .‎ A B C D E ‎1、‎ 提示：证明角的不等关系应当利用 ‎“三角形一个外角大于任何一个 与它不相邻的内角” 由此可得证。‎ A B C D E F ‎2、‎ ‎ 提示：此题的结论与图形，不难发现 ‎，‎ 因此须设法把它们联系起来，而三角形内角和定理正好将二者起来。‎