2020九年级数学下册 第26章二次函数的图象与性质 6页

‎26．2　二次函数的图象与性质 ‎2．二次函数y＝ax2＋bx＋c的图象与性质 第3课时　二次函数y＝a(x－h)2＋k的图象与性质 知|识|目|标 ‎1．通过阅读、操作、观察，能用描点法画二次函数y＝a(x－h)2＋k的图象. ‎ ‎2．通过比较、思考、讨论，能归纳出二次函数y＝a(x－h)2＋k图象的平移规律，并能确定平移后对应的函数关系式．‎ ‎3．在准确画出二次函数y＝a(x－h)2＋k的图象的基础上，通过观察、探究、合作交流，能总结出二次函数y＝a(x－h)2＋k的性质并会熟练应用．‎ 目标一　会画二次函数y＝a(x－h)2＋k的图象 例1 教材补充例题 在同一平面直角坐标系中画出下列函数的图象，并指出它们的开口方向、对称轴和顶点坐标．‎ y＝x2，y＝(x－1)2，y＝(x－1)2－2.‎ ‎【归纳总结】画二次函数y＝a(x－h)2＋k的图象的技巧：‎ ‎(1)找到对称轴直线x＝h(即顶点的横坐标h)；‎ ‎(2)列表时选取的x值中把h放在中间，比h小和比h大的数各取若干个(一般取整数)，并求出对应的y的值；‎ ‎(3)在平面直角坐标系里描出表中以(x，y)为坐标的点，并用光滑的曲线顺次连结．‎ 目标二　掌握二次函数图象的平移规律 例2 教材补充例题 (1)把抛物线y＝x2先向右平移2个单位，再向上平移3‎ 6‎ 个单位，平移后抛物线的关系式是____________；‎ ‎(2)将抛物线y＝3(x－4)2＋2先向右平移1个单位，再向下平移3个单位，平移后的抛物线的关系式是____________．‎ ‎【归纳总结】求平移后的抛物线对应的函数关系式的方法：‎ 首先要将二次函数的关系式化为顶点式，然后按照“左加右减，上加下减”的平移规律，确定平移后的抛物线对应的函数关系式．‎ 目标三　理解二次函数y＝a(x－h)2＋k的性质 例3 高频考题 已知函数y＝3＋9.‎ ‎(1)确定此函数图象的开口方向、对称轴和顶点坐标；‎ ‎(2)当x＝________时，函数有最________值，是________；‎ ‎(3)当x________时，y随x的增大而增大；当x________时，y随x的增大而减小；‎ ‎(4)求出该函数图象与y轴的交点坐标．‎ ‎【归纳总结】二次函数y＝a(x－h)2＋k的性质：‎ 二次函数y＝a(x－h)2＋k的图象是一条抛物线，它的开口方向、对称轴和顶点坐标与a，h，k的值有关．‎ ‎(1)当a＞0时，开口向上；当a＜0时，开口向下．‎ ‎(2)对称轴是直线x＝h.‎ ‎(3)顶点坐标是(h，k)．‎ ‎(4)当x＝h时，函数有最大(或最小)值k.‎ ‎(5)若a>0，则当x＜h时，y随x的增大而减小，当x>h时，y随x的增大而增大；若a<0，则当x＜h时，y随x的增大而增大，当x>h时，y随x的增大而减小．‎ 知识点一　二次函数y＝a(x－h)2＋k的图象与二次函数y＝ax2的图象的关系 ‎(1)形如y＝a(x－h)2＋k(a≠0)的关系式叫做二次函数的顶点式．二次函数y＝a(x－h)2＋k的图象与二次函数y＝ax2的图象形状完全________，但位置不同，其顶点坐标为________，对称轴为直线________．‎ ‎(2)二次函数y＝a(x－h)2＋k的图象可由二次函数y＝ax2的图象向右平移h(h>0)个单位[或向左平移|h|(h＜0)个单位]，再向上平移k(k>0)个单位[或向下平移|k|(k<0)个单位]得到．‎ 知识点二　二次函数y＝a(x－h)2＋k的图象与性质 二次函数 a的符号 图象 图象的开口方向 图象的对称轴 图象的顶点坐标 函数值的变化情况 最值 6‎ 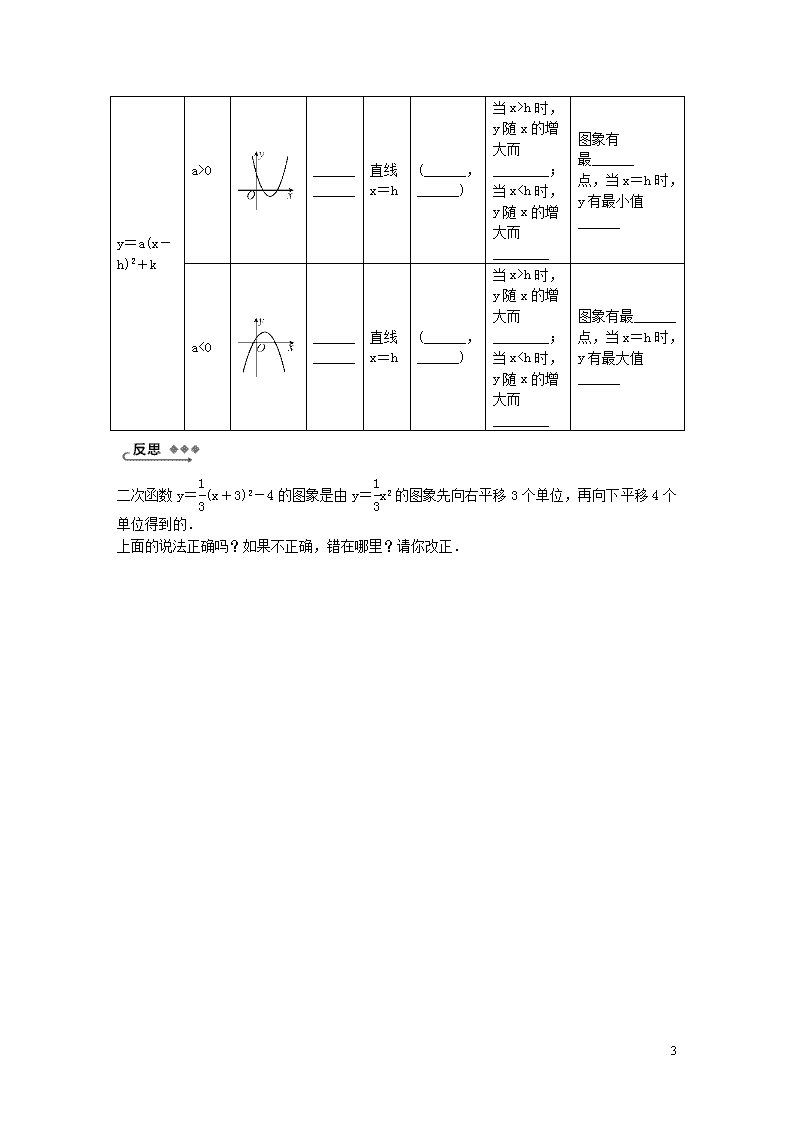y＝a(x－h)2＋k a>0‎ ‎______‎ ‎______‎ 直线 x＝h ‎(______，‎ ‎______)‎ 当x>h时，y随x的增大而________；当xh时，y随x的增大而________；当x2　<2‎ ‎(4)该函数图象与y轴的交点坐标为(0，21)．‎ ‎[备选例题] 把抛物线y＝－x2向左平移3个单位，再向上平移4个单位，得到一条新抛物线．‎ ‎(1)求所得到的新抛物线对应的函数关系式；‎ ‎(2)求所得到的新抛物线的开口方向、对称轴和顶点坐标；‎ ‎(3)当x取何值时，新抛物线对应的函数值y随着x的增大而增大？当x取何值时，新抛物线对应的函数值y随着x的增大而减小？‎ ‎(4)求出新抛物线对应的函数的最大值和最小值．‎ 6‎ 解：(1)y＝－(x＋3)2＋4.‎ ‎(2)因为a＝－<0，所以新抛物线的开口向下，对称轴是直线x＝－3，顶点坐标是(－3，4)．‎ ‎(3)当x<－3时，y随着x的增大而增大；‎ 当x>－3时，y随着x的增大而减小．‎ ‎(4)因为a＝－<0，所以y有最大值，当x＝－3时，y有最大值4，无最小值．‎ ‎【总结反思】‎ ‎[小结] 知识点一　(1)相同　(h，k)　x＝h 知识点二　向上　h　k　增大　减小　低　k　向下　h　k　减小　增大　高　k ‎[反思] 不正确，混淆了左右平移．‎ 改正：二次函数y＝(x＋3)2－4的图象是由y＝x2的图象先向左平移3个单位，再向下平移4个单位得到的．‎ 6‎ 6‎