五年级上册数学教案-6组合图形面积｜冀教版 (5) 4页

‎“组合图形的面积”教学活动设计 ‎ ‎ 课 题 组合图形的面积 课型 新授 教材分析 ‎《组合图形的面积》是第六单元的最后一个学习内容，是学生学习了长方形、正方形、平行四边形、三角形、梯形面积的基础上，对这些知识的延展，也是实际生活中解决问题的需要。在已有知识的基础上学习组合图形，一方面可以巩固基本图形的面积计算，另一方面还能将所学知识加以综合运用，提高学生解决实际问题的能力。儿童思维发展的一般规律是从具体操作开始的，再逐步形成抽象的思维。教学设计时，充分考虑儿童的原有认知水平及儿童心理发展水平，放手让学生自主探究，注重让学生在观察、操作、合作交流、比较等数学活动中，找出计算组合图形面积的多种方法，并进行优化选择。学生在解决问题的过程中，获得数学学习方法，在对学习过程与结果的反思中，提高解决问题的能力。‎ 学情分析 ‎《组合图形的面积》是学生在已经学习了长方形、正方形、平行四边形、三角形与梯形面积计算的基础上进行教学的。学生已初步具备了一定的空间思维能力，但只局限于对单一图形进行简单分析。本节课通过巩固已有知识，提高学生综合实践能力，有利于进一步发展学生的空间观念，同时让学生在数学思想方法及解决问题的思考策略方面有所发展。‎ 教学目标 ‎1.通过画一画活动，掌握用“割”、“补”的方法，形成组合图形面积计算的策略。‎ ‎2.能根据各种组合图形的条件，自主探究问题解决的方法。‎ ‎3.在自主探索、解决问题的过程中，感受策略获得的成功喜悦，形成方法多样、合理优化的问题解决策略。‎ ‎4.能运用所学知识，解决生活中组合图形的实际问题，感受数学知识的广泛应用。‎ 教学重点 将组合图形“割”“补”成几个基本图形，并能在图中找出适用的长度数据计算出组合图形的面积。‎ 教学难点 合理利用图中的已知数据，找出合理的割补方法，求出组合图形的面积。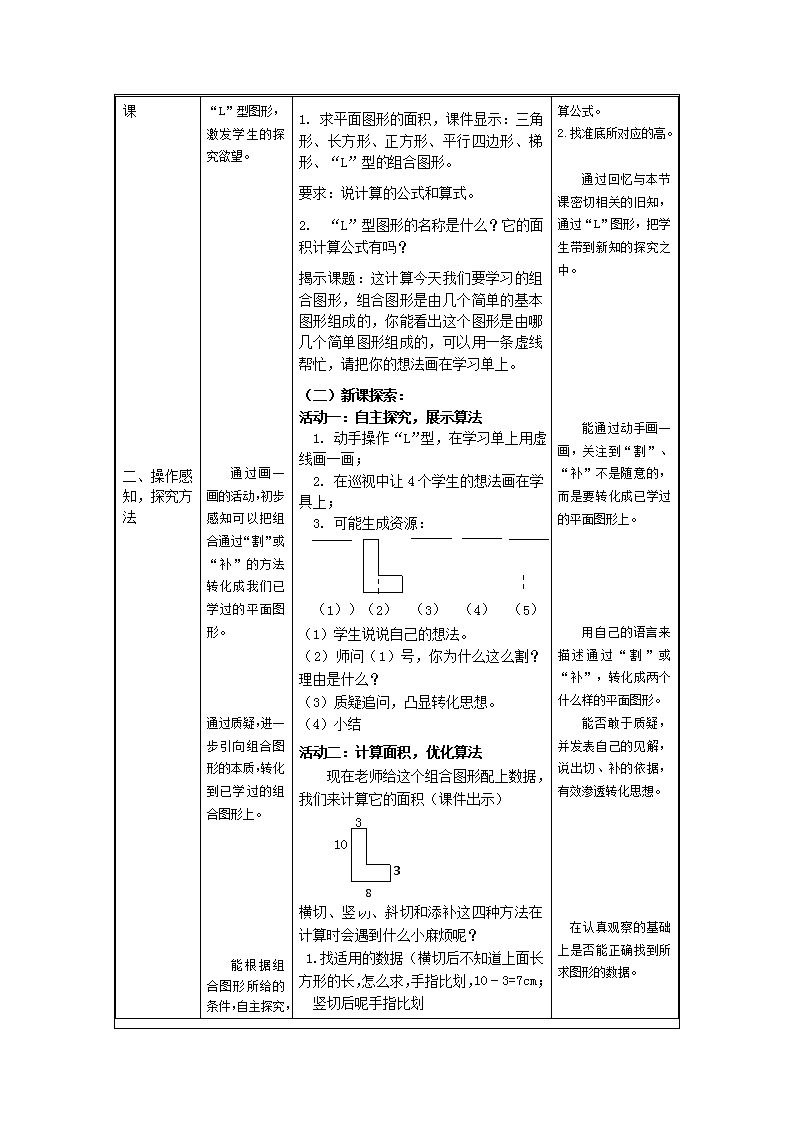‎ 课前准备 多媒体课件、学习用具、学习单 教学 环节 教 学 过 程 目标指向 师生活动 评价关注点 一、复习铺垫，引入新 ‎ 从旧知引入 ‎（一）复习导入：‎ ‎1.正确说出图形的计 课 二、操作感知，探究方法 ‎“L”型图形，激发学生的探究欲望。‎ 通过画一画的活动，初步感知可以把组合通过“割”或“补”的方法转化成我们已学过的平面图形。‎ 通过质疑，进一步引向组合图形的本质，转化到已学过的组合图形上。‎ ‎1. 求平面图形的面积，课件显示：三角形、长方形、正方形、平行四边形、梯形、“L”型的组合图形。‎ 要求：说计算的公式和算式。‎ 2. ‎ “L”型图形的名称是什么？它的面积计算公式有吗？‎ 揭示课题：这计算今天我们要学习的组合图形，组合图形是由几个简单的基本图形组成的，你能看出这个图形是由哪几个简单图形组成的，可以用一条虚线帮忙，请把你的想法画在学习单上。‎ ‎（二）新课探索：‎ 活动一：自主探究，展示算法 1. 动手操作“L”型，在学习单上用虚线画一画；‎ 2. 在巡视中让4个学生的想法画在学具上；‎ 3. 可能生成资源：‎ ‎（1））（2） （3） （4） （5）‎ （1） 学生说说自己的想法。‎ ‎（2）师问（1）号，你为什么这么割？理由是什么？‎ ‎（3）质疑追问，凸显转化思想。‎ ‎（4）小结 活动二：计算面积，优化算法 现在老师给这个组合图形配上数据，我们来计算它的面积（课件出示）‎ ‎ 3‎ ‎3‎ ‎ 10‎ ‎ ‎ ‎8‎ 横切、竖切、斜切和添补这四种方法在计算时会遇到什么小麻烦呢？‎ ‎ 1.找适用的数据（横切后不知道上面长方形的长，怎么求，手指比划，10﹣3=7cm；‎ 竖切后呢手指比划 算公式。‎ ‎2.找准底所对应的高。‎ 通过回忆与本节课密切相关的旧知，通过“L”图形，把学生带到新知的探究之中。‎ 能通过动手画一画，关注到“割”、“补”不是随意的，而是要转化成已学过的平面图形上。‎ ‎ ‎ ‎ ‎ 用自己的语言来描述通过“割”或“补”，转化成两个什么样的平面图形。‎ 能否敢于质疑，并发表自己的见解，说出切、补的依据，有效渗透转化思想。‎ ‎ ‎ ‎ ‎ 在认真观察的基础上是否能正确找到所求图形的数据。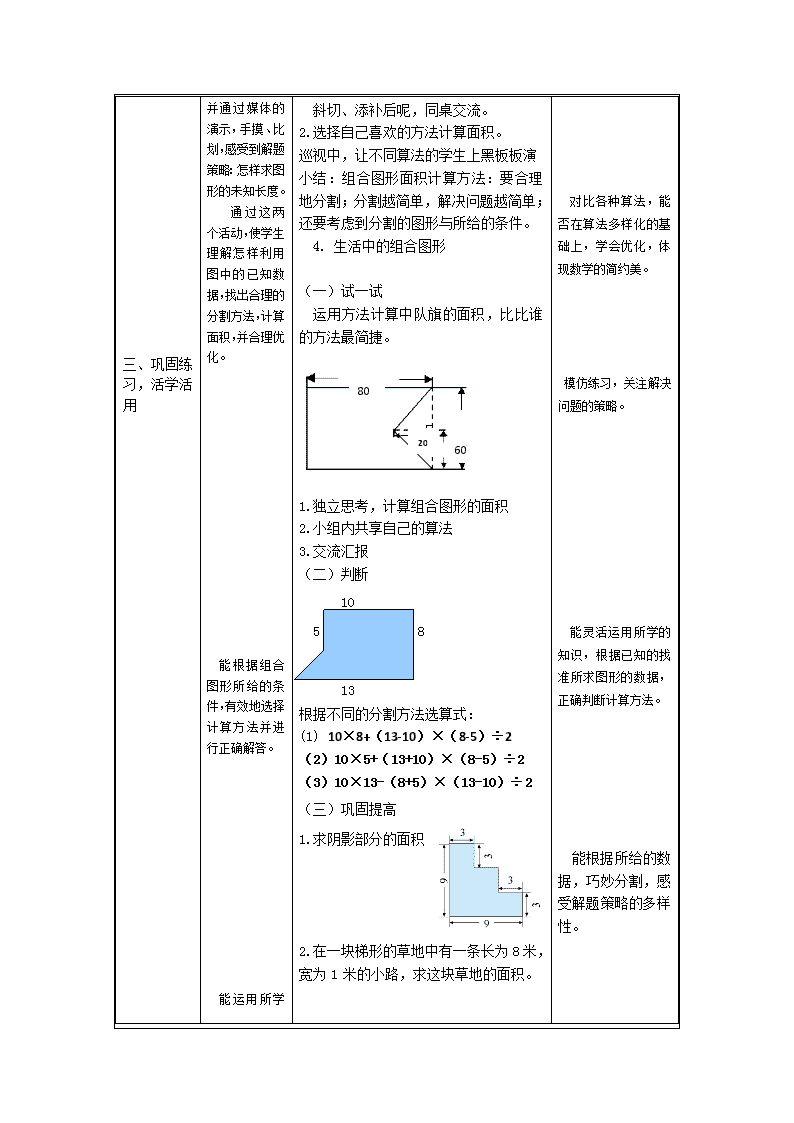‎ 三、巩固练习，活学活用 能根据组合图形所给的条件，自主探究，并通过媒体的演示，手摸、比划，感受到解题策略：怎样求图形的未知长度。‎ 通过这两个活动，使学生理解怎样利用图中的已知数据，找出合理的分割方法，计算面积，并合理优化。‎ 能根据组合图形所给的条件，有效地选择计算方法并进行正确解答。‎ 能运用所学 斜切、添补后呢，同桌交流。‎ ‎2.选择自己喜欢的方法计算面积。‎ 巡视中，让不同算法的学生上黑板板演 小结：组合图形面积计算方法：要合理地分割；分割越简单，解决问题越简单；还要考虑到分割的图形与所给的条件。‎ 1. 生活中的组合图形 ‎（一）试一试 运用方法计算中队旗的面积，比比谁的方法最简捷。‎ ‎80‎ ‎20‎ ‎60‎ ‎1.独立思考，计算组合图形的面积 ‎2.小组内共享自己的算法 ‎3.交流汇报 ‎（二）判断 ‎ 10‎ ‎ 5 8‎ ‎ 13‎ 根据不同的分割方法选算式：‎ ‎(1) 10×8+（13-10）×（8-5）÷2‎ ‎（2）10×5+（13+10）×（8-5）÷2‎ ‎（3）10×13-（8+5）×（13-10）÷2‎ ‎（三）巩固提高 ‎1.求阴影部分的面积 ‎2.在一块梯形的草地中有一条长为8米，宽为1米的小路，求这块草地的面积。‎ ‎ ‎ 对比各种算法，能否在算法多样化的基础上，学会优化，体现数学的简约美。‎ ‎ 模仿练习，关注解决问题的策略。 ‎ 能灵活运用所学的知识，根据已知的找准所求图形的数据，正确判断计算方法。‎ 能根据所给的数据，巧妙分割，感受解题策略的多样性。‎ 四、总结梳理，思维拓展 知识，解决生活中组合图形的实际问题，感受数学知识的广泛应用。‎ 在总结梳理里中，提升求组合的方法，拓展学生的思维。‎ 师：今天我们学习的组合图形的面积，你们用了哪些方法？还有什么方法 我们一起回过头来看“L”～‎ 因为这个图形的橫宽和竖宽都是3厘米 课件展示：‎ 横切后把两个长方形拼成一个大长方形 竖切后把两个长方形拼成一个大长方形 斜切后可以把两个梯形拼成一个平行四边形、一个大梯形或一个长方形 通过割、平移、旋转，转化成了我们已学过的图形……‎ 在总结回顾中，关注学生方法的掌握，以及课件的展示，拓宽学生的思路，为后续的学习打下基础。‎ 反思与重构 板书设计 组合图形的面积 ‎（横切、竖切、斜切）‎ 分割法 添补法 切拼法 ‎ 转化 ‎ 基本图形（找准数据 合理分割）‎