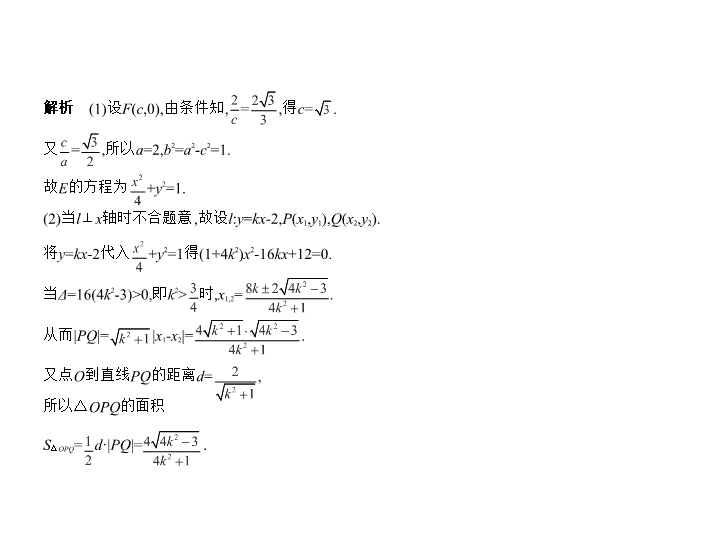高考理数　椭圆及其性质 68页

§10.1 　椭圆及其性质 高考理数 ( 课标专用) 考点一　椭圆的定义和标准方程 1. (2014课标Ⅰ,20,12分,0.433)已知点 A (0,-2),椭圆 E :   +   =1( a > b >0)的离心率为   , F 是椭圆 E 的右焦点,直线 AF 的斜率为   , O 为坐标原点. (1)求 E 的方程; (2)设过点 A 的动直线 l 与 E 相交于 P , Q 两点.当△ OPQ 的面积最大时,求 l 的方程. A组  统一命题·课标卷题组 五年高考 解析 　(1)设 F ( c ,0),由条件知,   =   ,得 c =   . 又   =   ,所以 a =2, b 2 = a 2 - c 2 =1. 故 E 的方程为   + y 2 =1. (2)当 l ⊥ x 轴时不合题意,故设 l : y = kx -2, P ( x 1 , y 1 ), Q ( x 2 , y 2 ). 将 y = kx -2代入   + y 2 =1得(1+4 k 2 ) x 2 -16 kx +12=0. 当 Δ =16(4 k 2 -3)>0,即 k 2 >   时, x 1,2 =   . 从而| PQ |=   | x 1 - x 2 |=   . 又点 O 到直线 PQ 的距离 d =   , 所以△ OPQ 的面积 S △ OPQ =   d ·| PQ |=   . 设   = t ,则 t >0, S △ OPQ =   =   . 因为 t +   ≥ 4,当且仅当 t =2,即 k = ±   时等号成立,且满足 Δ >0, 所以,当△ OPQ 的面积最大时, l 的方程为 y =   x -2或 y =-   x -2. 思路分析 　(1)通过直线 AF 的斜率求得 c 的值,通过离心率求得 a ,进而求出 b 2 ,从而得到 E 的方程; (2)设出直线 l 的方程和点 P 、 Q 的坐标,联立直线 l 与椭圆方程,利用弦长公式求得| PQ |的长,根据 点到直线的距离公式求得△ OPQ 边 PQ 上的高,从而表示出△ OPQ 的面积,利用换元法和基本 不等式即可得到当面积取得最大值时 k 的值,从而得直线 l 的方程. 解题关键 　对于第(2)问,正确选择参数,表示出△ OPQ 的面积,进而巧妙利用换元法分析最值 是解题的关键. 2. (2014课标Ⅱ,20,12分,0.185)设 F 1 , F 2 分别是椭圆 C :   +   =1( a > b >0)的左,右焦点, M 是 C 上一点 且 MF 2 与 x 轴垂直.直线 MF 1 与 C 的另一个交点为 N . (1)若直线 MN 的斜率为   ,求 C 的离心率; (2)若直线 MN 在 y 轴上的截距为2,且| MN |=5| F 1 N |,求 a , b . 解析 　(1)根据 c =   及题设知 M   ,2 b 2 =3 ac . 将 b 2 = a 2 - c 2 代入2 b 2 =3 ac ,解得   =   或   =-2(舍去). 故 C 的离心率为   . (2)由题意,得原点 O 为 F 1 F 2 的中点, MF 2 ∥ y 轴,所以直线 MF 1 与 y 轴的交点 D (0,2)是线段 MF 1 的中 点,故   =4,即 b 2 =4 a .   ① 由| MN |=5| F 1 N |得| DF 1 |=2| F 1 N |. 设 N ( x 1 , y 1 ),由题意知 y 1 <0, 则   即   代入 C 的方程,得   +   =1.   ② 将①及 c =   代入②得   +   =1. 解得 a =7,故 b 2 =4 a =28,故 a =7, b =2   . 考点二　椭圆的几何性质 1. (2018课标Ⅱ,12,5分)已知 F 1 , F 2 是椭圆 C :   +   =1( a > b >0)的左、右焦点, A 是 C 的左顶点,点 P 在过 A 且斜率为   的直线上,△ PF 1 F 2 为等腰三角形,∠ F 1 F 2 P =120 ° ,则 C 的离心率为   (　　) A.   　    B.   　    C.   　    D.   答案    D 　本题考查直线方程和椭圆的几何性质. 由题意易知直线 AP 的方程为 y =   ( x + a ),① 直线 PF 2 的方程为 y =   ( x - c ).② 联立①②得 y =   ( a + c ), 如图,过 P 向 x 轴引垂线,垂足为 H ,则 PH =   ( a + c ).   因为∠ PF 2 H =60 ° , PF 2 = F 1 F 2 =2 c , PH =   ( a + c ), 所以sin 60 ° =   =   =   , 即 a + c =5 c ,即 a =4 c , 所以 e =   =   .故选D. 解题关键 　通过解三角形得到 a 与 c 的等量关系是解题的关键. 2. (2017课标Ⅲ,10,5分)已知椭圆 C :   +   =1( a > b >0)的左、右顶点分别为 A 1 , A 2 ,且以线段 A 1 A 2 为 直径的圆与直线 bx - ay +2 ab =0相切,则 C 的离心率为   (　　) A.   　    B.   　    C.   　    D.   答案    A　 本题考查椭圆的性质,直线与圆的位置关系. 以线段 A 1 A 2 为直径的圆的方程为 x 2 + y 2 = a 2 ,该圆与直线 bx - ay +2 ab =0相切, ∴   = a ,即2 b =   , ∴ a 2 =3 b 2 ,∵ a 2 = b 2 + c 2 , ∴   =   ,∴ e =   =   . 方法技巧 　椭圆离心率的求法: (1)定义法:根据条件求出 a , c ,直接利用公式 e =   求解. (2)方程法:根据已知条件建立关于 a , b , c 的齐次式,然后转化为关于 e 的方程求解.注意要根据 e 的 范围取舍方程的解. 3. (2016课标Ⅲ,11,5分)已知 O 为坐标原点, F 是椭圆 C :   +   =1( a > b >0)的左焦点, A , B 分别为 C 的 左,右顶点. P 为 C 上一点,且 PF ⊥ x 轴.过点 A 的直线 l 与线段 PF 交于点 M ,与 y 轴交于点 E .若直线 BM 经过 OE 的中点,则 C 的离心率为       (　　) A.   　    B.   　    C.   　    D.   答案    A　 由题意知过点 A 的直线 l 的斜率存在且不为0,故可设直线 l 的方程为 y = k ( x + a ),当 x =- c 时, y = k ( a - c ),当 x =0时, y = ka ,所以 M (- c , k ( a - c )), E (0, ka ).如图,设 OE 的中点为 N ,则 N   ,由于 B , M , N 三点共线,所以 k BN = k BM ,即   =   ,所以   =   ,即 a =3 c ,所以 e =   .故选A.   思路分析 　根据题意设出过点 A 的直线 l 的方程,从而求出点 M 和点 E 的坐标,进一步写出线段 OE 中点的坐标,利用三点共线建立关于 a , c 的方程,得到 a , c 的关系式,从而求出椭圆的离心率.求 解本题的关键在于写出各对应点的坐标,难点在于参数的选择. 方法点拨 　求解圆锥曲线的离心率问题的关键是要通过其几何性质找到 a , c 所满足的关系,从 而利用 e =   求得离心率. 4. (2018课标Ⅲ,20,12分)已知斜率为 k 的直线 l 与椭圆 C :   +   =1交于 A , B 两点,线段 AB 的中点为 M (1, m )( m >0). (1)证明: k <-   ; (2)设 F 为 C 的右焦点, P 为 C 上一点,且   +   +   =0.证明:|   |,|   |,|   |成等差数列,并求该数 列的公差. 解析 　本题考查椭圆的几何性质、直线与椭圆的位置关系、等差数列的概念及其运算. (1)设 A ( x 1 , y 1 ), B ( x 2 , y 2 ), 则   +   =1,   +   =1. 两式相减,并由   = k 得   +   · k =0. 由题设知   =1,   = m , 于是 k =-   .   ① 由题设得0< m <   ,故 k <-   . (2)由题意得 F (1,0). 设 P ( x 3 , y 3 ), 则( x 3 -1, y 3 )+( x 1 -1, y 1 )+( x 2 -1, y 2 )=(0,0). 由(1)及题设得 x 3 =3-( x 1 + x 2 )=1, y 3 =-( y 1 + y 2 )=-2 m <0. 又点 P 在 C 上, 所以 m =   , 从而 P   ,|   |=   . 于是|   |=   =   =2-   . 同理,|   |=2-   . 所以|   |+|   |=4-   ( x 1 + x 2 )=3. 故2|   |=|   |+|   |, 即|   |,|   |,|   |成等差数列. 设该数列的公差为 d ,则 2| d |=||   |-|   ||=   | x 1 - x 2 |=     .   ② 将 m =   代入①得 k =-1. 所以 l 的方程为 y =- x +   ,代入 C 的方程,并整理得7 x 2 -14 x +   =0. 故 x 1 + x 2 =2, x 1 x 2 =   ,代入②解得| d |=   . 所以该数列的公差为   或-   . 思路分析 　(1)利用“点差法”建立 k 与 m 的关系式,由 m 的范围得到 k 的范围. (2)根据题设   +   +   =0及点 P 在 C 上,确定 m 的值.进一步得出|   |、|   |、|   |的关系,再求 公差. 解后反思 　(1)解决直线与椭圆的位置关系的常规思路是先把直线方程与椭圆方程联立,消 元、化简,然后利用根与系数的关系建立方程(组),解决相关问题. (2)题中涉及弦的中点坐标时,可以采用“点差法”求解,设出弦端点 A 、 B 的坐标,分别代入圆 锥曲线方程并作差,变形后可出现弦 AB 的中点坐标和直线 AB 的斜率. 考点一　椭圆的定义和标准方程 1 .(2014大纲全国,6,5分)已知椭圆 C :   +   =1( a > b >0)的左、右焦点为 F 1 、 F 2 ,离心率为   ,过 F 2 的直线 l 交 C 于 A 、 B 两点.若△ AF 1 B 的周长为4   ,则 C 的方程为   (　　) A.   +   =1　    B.   + y 2 =1　    C.   +   =1　    D.   +   =1 B组  自主命题·省(区、市)卷题组 答案    A　 由题意及椭圆的定义知4 a =4   ,则 a =   ,又   =   =   ,∴ c =1,∴ b 2 =2,∴ C 的方程为   +   =1,选A. 2. (2014安徽,14,5分)设 F 1 , F 2 分别是椭圆 E : x 2 +   =1(0< b <1)的左、右焦点,过点 F 1 的直线交椭圆 E 于 A , B 两点.若| AF 1 |=3| F 1 B |, AF 2 ⊥ x 轴,则椭圆 E 的方程为 　　　　     . 答案      x 2 +   y 2 =1 解析 　不妨设点 A 在第一象限,∵ AF 2 ⊥ x 轴,∴ A ( c , b 2 )(其中 c 2 =1- b 2 ,0< b <1, c >0). 由| AF 1 |=3| F 1 B |,得   =3   , 进而可得 B   , 代入 x 2 +   =1得   +   =1, 又 c 2 =1- b 2 ,∴ b 2 =   . 故椭圆 E 的方程为 x 2 +   y 2 =1. 3. (2015陕西,20,12分)已知椭圆 E :   +   =1( a > b >0)的半焦距为 c ,原点 O 到经过两点( c ,0),(0, b )的 直线的距离为   c . (1)求椭圆 E 的离心率; (2)如图, AB 是圆 M :( x +2) 2 +( y -1) 2 =   的一条直径,若椭圆 E 经过 A , B 两点,求椭圆 E 的方程.   解析 　(1)过点( c ,0),(0, b )的直线方程为 bx + cy - bc =0, 则原点 O 到该直线的距离 d =   =   , 由 d =   c ,得 a =2 b =2   ,可得离心率   =   . (2)解法一:由(1)知,椭圆 E 的方程为 x 2 +4 y 2 =4 b 2 .① 依题意,圆心 M (-2,1)是线段 AB 的中点,且| AB |=   . 易知, AB 与 x 轴不垂直,设其方程为 y = k ( x +2)+1,代入①得 (1+4 k 2 ) x 2 +8 k (2 k +1) x +4(2 k +1) 2 -4 b 2 =0. 设 A ( x 1 , y 1 ), B ( x 2 , y 2 ), 则 x 1 + x 2 =-   , x 1 x 2 =   . 由 x 1 + x 2 =-4,得-   =-4, 解得 k =   . 从而 x 1 x 2 =8-2 b 2 . 于是| AB |=   | x 1 - x 2 | =     =   . 由| AB |=   ,得   =   ,解得 b 2 =3. 故椭圆 E 的方程为   +   =1. 解法二:由(1)知,椭圆 E 的方程为 x 2 +4 y 2 =4 b 2 .② 依题意,点 A , B 关于圆心 M (-2,1)对称,且| AB |=   . 设 A ( x 1 , y 1 ), B ( x 2 , y 2 ), 则   +4   =4 b 2 ,   +4   =4 b 2 , 两式相减并结合 x 1 + x 2 =-4, y 1 + y 2 =2,得 -4( x 1 - x 2 )+8( y 1 - y 2 )=0, 易知 AB 与 x 轴不垂直,则 x 1 ≠ x 2 , 所以 AB 的斜率 k AB =   =   . 因此直线 AB 的方程为 y =   ( x +2)+1, 代入②得 x 2 +4 x +8-2 b 2 =0. 所以 x 1 + x 2 =-4, x 1 x 2 =8-2 b 2 . 于是| AB |=   | x 1 - x 2 | =     =   . 由| AB |=   ,得   =   , 解得 b 2 =3. 故椭圆 E 的方程为   +   =1. 解题关键 　对于第(2)问,利用弦长及韦达定理或点差法构造关于参数的方程是解题的关键. 4. (2015安徽,20,13分)设椭圆 E 的方程为   +   =1( a > b >0),点 O 为坐标原点,点 A 的坐标为( a ,0), 点 B 的坐标为(0, b ),点 M 在线段 AB 上,满足| BM |=2| MA |,直线 OM 的斜率为   . (1)求 E 的离心率 e ; (2)设点 C 的坐标为(0,- b ), N 为线段 AC 的中点,点 N 关于直线 AB 的对称点的纵坐标为   ,求 E 的方 程. 解析 　(1)由题设条件知,点 M 的坐标为   , 又 k OM =   ,从而   =   . 进而得 a =   b , c =   =2 b .故 e =   =   . (2)由题设条件和(1)的计算结果可得,直线 AB 的方程为   +   =1,点 N 的坐标为   . 设点 N 关于直线 AB 的对称点 S 的坐标为   ,则线段 NS 的中点 T 的坐标为   . 又点 T 在直线 AB 上,且 k NS · k AB =-1,从而有   解得 b =3. 所以 a =3   ,故椭圆 E 的方程为   +   =1. 评析 　本题考查椭圆的方程、几何性质以及对称问题,利用方程思想解决点关于直线的对称 问题,考查利用待定系数法求椭圆的方程,考查学生的运算求解能力和化归思想的应用. 考点二　椭圆的几何性质 1. (2017浙江,2,5分)椭圆   +   =1的离心率是   (　　) A.   　    B.   　    C.   　    D.   答案    B 　本题考查椭圆的标准方程和几何性质. 由题意得, a =3, c =   ,∴离心率 e =   =   .故选B. 易错警示 　1.把椭圆和双曲线中的 a , b , c 之间的关系式记混,而错选A. 2.把离心率记成 e =   或 e =   ,而错选C或D. 2. (2014江西,15,5分)过点 M (1,1)作斜率为-   的直线与椭圆 C :   +   =1( a > b >0)相交于 A , B 两点, 若 M 是线段 AB 的中点,则椭圆 C 的离心率等于 　　　     . 答案        解析　 设 A ( x 1 , y 1 ), B ( x 2 , y 2 ),则   +   =1①,   +   =1②. ①、②两式相减并整理得   =-   ·   . 结合已知条件得,-   =-   ×   , ∴   =   ,故椭圆的离心率 e =   =   . 评析　 本题考查了直线和椭圆的位置关系.考查了线段的中点问题,利用整体运算的技巧是求 解的关键.本题也可以利用韦达定理求解. 3. (2018北京,14,5分)已知椭圆 M :   +   =1( a > b >0),双曲线 N :   -   =1.若双曲线 N 的两条渐近 线与椭圆 M 的四个交点及椭圆 M 的两个焦点恰为一个正六边形的顶点,则椭圆 M 的离心率为 　　     ;双曲线 N 的离心率为 　　　     . 答案        -1;2 解析　 本题考查椭圆与双曲线的几何性质. 解法一:如图是一个正六边形, A , B , C , D 是双曲线 N 的两条渐近线与椭圆 M 的四个交点, F 1 , F 2 为椭 圆 M 的两个焦点.   ∵直线 AC 是双曲线 N 的一条渐近线,且其方程为 y =   x , ∴   =   .设 m = k ,则 n =   k ,则双曲线 N 的离心率 e 2 =   =2. 连接 F 1 C ,在正六边形 ABF 2 CDF 1 中,可得∠ F 1 CF 2 =90 ° ,∠ CF 1 F 2 =30 ° . 设椭圆的焦距为2 c ,则| CF 2 |= c ,| CF 1 |=   c ,再由椭圆的定义得| CF 1 |+| CF 2 |=2 a ,即(   +1) c =2 a ,∴椭 圆 M 的离心率 e 1 =   =   =   =   -1. 解法二:双曲线 N 的离心率同解法一.由题意可得 C 点坐标为   ,代入椭圆 M 的方程,并结 合 a , b , c 的关系,联立得方程组   解得   =   -1   . 方法总结 　求椭圆和双曲线的离心率的关键是通过其几何性质找到 a , c 所满足的关系,从而求 出 c 与 a 的比值,即得离心率. 4. (2014江苏,17,14分)如图,在平面直角坐标系 xOy 中, F 1 、 F 2 分别是椭圆   +   =1( a > b >0)的 左、右焦点,顶点 B 的坐标为(0, b ),连接 BF 2 并延长交椭圆于点 A ,过点 A 作 x 轴的垂线交椭圆于另 一点 C ,连接 F 1 C . (1)若点 C 的坐标为   ,且 BF 2 =   ,求椭圆的方程; (2)若 F 1 C ⊥ AB ,求椭圆离心率 e 的值.   解析 　设椭圆的焦距为2 c ,则 F 1 (- c ,0), F 2 ( c ,0). (1)因为 B (0, b ),所以 BF 2 =   = a . 又 BF 2 =   ,故 a =   . 因为点 C   在椭圆上, 所以   +   =1,解得 b 2 =1.故所求椭圆的方程为   + y 2 =1. (2)因为 B (0, b ), F 2 ( c ,0)在直线 AB 上, 所以直线 AB 的方程为   +   =1. 解方程组   得     所以点 A 的坐标为   . 又 AC 垂直于 x 轴,由椭圆的对称性,可得点 C 的坐标为   . 因为直线 F 1 C 的斜率为   =   ,直线 AB 的斜率为-   ,且 F 1 C ⊥ AB ,所以   ·   =-1.结合 b 2 = a 2 - c 2 ,整理得 a 2 =5 c 2 .故 e 2 =   .因此 e =   . 5 .(2015重庆,21,12分)如图,椭圆   +   =1( a > b >0)的左、右焦点分别为 F 1 , F 2 ,过 F 2 的直线交椭圆 于 P , Q 两点,且 PQ ⊥ PF 1 . (1)若| PF 1 |=2+   ,| PF 2 |=2-   ,求椭圆的标准方程; (2)若| PF 1 |=| PQ |,求椭圆的离心率 e .   解析　(1)由椭圆的定义,有2 a =| PF 1 |+| PF 2 |=(2+   )+(2-   )=4,故 a =2. 设椭圆的半焦距为 c ,由已知 PF 1 ⊥ PF 2 ,得2 c =| F 1 F 2 |=   =   =2   , 即 c =   ,从而 b =   =1. 故所求椭圆的标准方程为   + y 2 =1. (2)解法一:连接 F 1 Q ,如图,设 P ( x 0 , y 0 ),因为点 P 在椭圆上,且 PF 1 ⊥ PF 2 ,   所以   +   =1,   +   = c 2 , 求得 x 0 = ±     , y 0 = ±   . 由| PF 1 |=| PQ |>| PF 2 |得 x 0 >0, 从而| PF 1 | 2 =   +   =2( a 2 - b 2 )+2 a   =( a +   ) 2 . 由 PF 1 ⊥ PF 2 ,| PF 1 |=| PQ |,知| QF 1 |=   | PF 1 |. 因此(2+   )| PF 1 |=4 a , 即(2+   )( a +   )=4 a , 于是(2+   )(1+   )=4, 解得 e =   =   -   . 解法二:连接 F 1 Q ,由椭圆的定义,有| PF 1 |+| PF 2 |=2 a ,| QF 1 |+| QF 2 |=2 a .从而由| PF 1 |=| PQ |=| PF 2 |+| QF 2 |, 有| QF 1 |=4 a -2| PF 1 |.又由 PF 1 ⊥ PQ ,| PF 1 |=| PQ |,知| QF 1 |=   | PF 1 |, 因此,4 a -2| PF 1 |=   | PF 1 |,得| PF 1 |=2(2-   ) a ,从而| PF 2 |=2 a -| PF 1 |=2 a -2(2-   ) a =2(   -1) a . 由 PF 1 ⊥ PF 2 ,知| PF 1 | 2 +| PF 2 | 2 =| F 1 F 2 | 2 =(2 c ) 2 , 因此 e =   =   =   =   =   -   . 考点一　椭圆的定义和标准方程 1 .(2011课标,14,5分)在平面直角坐标系 xOy 中,椭圆 C 的中心为原点,焦点 F 1 , F 2 在 x 轴上,离心率 为   .过 F 1 的直线 l 交 C 于 A , B 两点,且△ ABF 2 的周长为16,那么 C 的方程为 　　　　     . C组    教师专用题组 答案        +   =1 解析 　设椭圆方程为   +   =1( a > b >0), 因为 AB 过 F 1 且 A 、 B 在椭圆上, 如图,则△ ABF 2 的周长为| AB |+| AF 2 |+| BF 2 | =| AF 1 |+| AF 2 |+| BF 1 |+| BF 2 | =4 a =16, ∴ a =4. 又离心率 e =   =   , ∴ c =2   , ∴ b 2 = a 2 - c 2 =8, ∴椭圆 C 的方程为   +   =1. 失分警示 　本题易将 a 求出后当成 a 2 ,从而得出错误方程   +   =1等. 评析     本题主要考查椭圆的定义和标准方程,以及离心率,属中等难度题. 2. (2016四川,20,13分)已知椭圆 E :   +   =1( a > b >0)的两个焦点与短轴的一个端点是直角三角 形的三个顶点,直线 l : y =- x +3与椭圆 E 有且只有一个公共点 T . (1)求椭圆 E 的方程及点 T 的坐标; (2)设 O 是坐标原点,直线 l '平行于 OT ,与椭圆 E 交于不同的两点 A , B ,且与直线 l 交于点 P .证明:存 在常数 λ ,使得| PT | 2 = λ | PA |·| PB |,并求 λ 的值. 解析　 (1)由已知, a =   b , 则椭圆 E 的方程为   +   =1. 由方程组   得3 x 2 -12 x +(18-2 b 2 )=0.① 方程①的判别式为 Δ =24( b 2 -3),由 Δ =0,得 b 2 =3, 此时方程①的解为 x =2, 所以椭圆 E 的方程为   +   =1. 点 T 坐标为(2,1). (2)由已知可设直线 l '的方程为 y =   x + m ( m ≠ 0), 由方程组   可得   所以 P 点坐标为   ,| PT | 2 =   m 2 . 设点 A , B 的坐标分别为 A ( x 1 , y 1 ), B ( x 2 , y 2 ). 由方程组   可得3 x 2 +4 mx +(4 m 2 -12)=0.② 方程②的判别式为 Δ =16(9-2 m 2 ), 由 Δ >0,解得-   < m <   . 由②得 x 1 + x 2 =-   , x 1 x 2 =   .所以| PA |=   =     , 同理| PB |=     . 所以| PA |·| PB |=     =     方法总结 　一般地,解直线与圆锥曲线相交的问题时,常常是联立方程转化为关于 x (或 y )的一 元二次方程,注意 Δ >0,再结合根与系数的关系进行解题. 评析     本题考查了直线与圆锥曲线相交的问题,解这类题常用方程的思想方法,并结合根与 系数的关系,两点间距离公式,难点是运算量比较大,注意运算技巧. 故存在常数 λ =   ,使得| PT | 2 = λ | PA |·| PB |. =     =   m 2 . 3. (2015福建,18,13分)已知椭圆 E :   +   =1( a > b >0)过点(0,   ),且离心率 e =   . (1)求椭圆 E 的方程; (2)设直线 l : x = my -1( m ∈R)交椭圆 E 于 A , B 两点,判断点 G   与以线段 AB 为直径的圆的位置 关系,并说明理由.   解析　 (1)由已知得   解得   所以椭圆 E 的方程为   +   =1. (2)解法一:设点 A ( x 1 , y 1 ), B ( x 2 , y 2 ), AB 的中点为 H ( x 0 , y 0 ). 由   得( m 2 +2) y 2 -2 my -3=0, 所以 y 1 + y 2 =   , y 1 y 2 =-   , 从而 y 0 =   . 所以| GH | 2 =   +   =   +   =( m 2 +1)   +   my 0 +   .   =   =   =   =(1+ m 2 )(   - y 1 y 2 ), 故| GH | 2 -   =   my 0 +(1+ m 2 ) y 1 y 2 +   =   -   +   =   >0, 所以| GH |>   . 故点 G   在以 AB 为直径的圆外. 解法二:设点 A ( x 1 , y 1 ), B ( x 2 , y 2 ),则   =   ,   =   . 由   得( m 2 +2) y 2 -2 my -3=0, 所以 y 1 + y 2 =   , y 1 y 2 =-   , 从而   ·   =     + y 1 y 2 =     + y 1 y 2 =( m 2 +1) y 1 y 2 +   m ( y 1 + y 2 )+   =   +   +   =   >0, 所以cos<   ,   >>0.又   ,   不共线,所以∠ AGB 为锐角. 故点 G   在以 AB 为直径的圆外. 评析 　本题主要考查椭圆、圆、直线与椭圆的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想. 考点二　椭圆的几何性质 1. (2012课标,4,5分)设 F 1 , F 2 是椭圆 E :   +   =1( a > b >0)的左,右焦点, P 为直线 x =   上一点,△ F 2 PF 1 是底角为30 ° 的等腰三角形,则 E 的离心率为   (　　) A.   　    B.   　    C.   　    D.   答案    C　 设直线 x =   a 与 x 轴交于点 Q ,由题意得∠ PF 2 Q =60 ° ,| F 2 P |=| F 1 F 2 |=2 c ,| F 2 Q |=   a - c ,∴   a - c =   × 2 c ,则 e =   =   ,故选C. 评析     本题考查了椭圆的基本性质,考查了方程的思想,灵活解三角形对求解至关重要. 2. (2013辽宁,15,5分)已知椭圆 C :   +   =1( a > b >0)的左焦点为 F , C 与过原点的直线相交于 A , B 两 点,连接 AF , BF .若| AB |=10,| AF |=6,cos∠ ABF =   ,则 C 的离心率 e = 　　     . 答案        解析　 如图,设右焦点为 F 1 ,| BF |= x ,则cos∠ ABF =   =   .   解得 x =8,故∠ AFB =90 ° .由椭圆 C 及直线 AB 关于原点对称可知| AF 1 |=8,且∠ FAF 1 =90 ° ,△ FAF 1 是 直角三角形,| F 1 F |=10,故2 a =8+6=14,2 c =10, e =   =   . 评析　本题考查椭圆的定义、几何性质、余弦定理等知识.注意椭圆的对称性是解题的关键. 3 .(2016浙江,19,15分)如图,设椭圆   + y 2 =1( a >1). (1)求直线 y = kx +1被椭圆截得的线段长(用 a , k 表示); (2)若任意以点 A (0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.   解析 　(1)设直线 y = kx +1被椭圆截得的线段为 AP , 由   得(1+ a 2 k 2 ) x 2 +2 a 2 kx =0, 故 x 1 =0, x 2 =-   . 因此| AP |=   | x 1 - x 2 |=   ·   . (2)假设圆与椭圆的公共点有4个,由对称性可设 y 轴左侧的椭圆上有两个不同的点 P , Q ,满足| AP |=| AQ |. 记直线 AP , AQ 的斜率分别为 k 1 , k 2 ,且 k 1 , k 2 >0, k 1 ≠ k 2 . 由(1)知,| AP |=   ,| AQ |=   , 故   =   , 所以(   -   )[1+   +   + a 2 (2- a 2 )    ]=0. 由于 k 1 ≠ k 2 , k 1 , k 2 >0得1+   +   + a 2 (2- a 2 )    =0, 因此    =1+ a 2 ( a 2 -2),   ① 因为①式关于 k 1 , k 2 的方程有解的充要条件是1+ a 2 ( a 2 -2)>1,所以 a >   . 因此,任意以点 A (0,1)为圆心的圆与椭圆至多有3个公共点的充要条件为1< a ≤   , 由 e =   =   得,所求离心率的取值范围为0< e ≤   . 评析　 本题主要考查椭圆的几何性质、直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力. 考点一　椭圆的定义和标准方程 1. (2018湖北重点中学4月联考,7)已知椭圆   +   =1的左、右焦点分别为 F 1 、 F 2 ,过 F 2 且垂直于 长轴的直线交椭圆于 A , B 两点,则△ ABF 1 内切圆的半径为   (　　) A.   　    B.1　    C.   　    D.   三年模拟 A组 201 6 —201 8 年 高考模拟·基础题 组 答案    D　 不妨设 A 点在 B 点上方,由题意知: F 2 (1,0),将 F 2 的横坐标代入椭圆方程   +   =1中,可 得 A 点纵坐标为   ,故| AB |=3,所以内切圆半径 r =   =   =   (其中 S 为△ ABF 1 的面积, C 为△ ABF 1 的 周长).故选D. 一题多解 　由椭圆的通径公式得| AB |=   =3,则   =   × 2 × 3=3,又易得△ ABF 1 的周长 C =4 a =8, 则由   =   C · r 可得 r =   .故选D. 2. (2017江西九江模拟,8) F 1 , F 2 是椭圆   +   =1的左、右焦点, A 为椭圆上一点,且∠ AF 1 F 2 =45 ° , 则△ AF 1 F 2 的面积为   (　　) A.7　    B.   　    C.   　    D.   答案    C 　由题意可得, a =3, b =   , c =   ,| AF 1 |+| AF 2 |=6. ∴| AF 2 |=6-| AF 1 |. 在△ AF 1 F 2 中,| AF 2 | 2 =| AF 1 | 2 +| F 1 F 2 | 2 -2| AF 1 |·| F 1 F 2 |·cos 45 ° =| AF 1 | 2 -4| AF 1 |+8, ∴(6-| AF 1 |) 2 =| AF 1 | 2 -4| AF 1 |+8, 解得| AF 1 |=   , ∴△ AF 1 F 2 的面积 S =   ×   × 2   ×   =   ,故选C. 3. (2016湖北荆门一模,11)已知 θ 是△ ABC 的一个内角,且sin θ +cos θ =   ,则方程 x 2 sin θ - y 2 cos θ =1 表示   (　　) A.焦点在 x 轴上的双曲线 B.焦点在 y 轴上的双曲线 C.焦点在 x 轴上的椭圆 D.焦点在 y 轴上的椭圆 答案    D 　因为(sin θ +cos θ ) 2 =1+2sin θ cos θ =   ,所以sin θ cos θ =-   <0,结合 θ ∈(0,π),知sin θ >0, cos θ <0,又sin θ +cos θ =   >0,所以sin θ >-cos θ >0,故   >   >0,因为 x 2 sin θ - y 2 cos θ =1可化为   +   =1,所以方程 x 2 sin θ - y 2 cos θ =1表示焦点在 y 轴上的椭圆. 4. (2018山西康杰中学4月月考,15)设 F 1 、 F 2 为椭圆 C :   +   =1( a > b >0)的左、右焦点,经过 F 1 的 直线交椭圆 C 于 A , B 两点,若△ F 2 AB 是面积为4   的等边三角形,则椭圆 C 的方程为 　　　　    　     . 答案        +   =1 解析 　∵△ F 2 AB 是面积为4   的等边三角形, ∴ AB ⊥ x 轴,∴ A , B 两点的横坐标为- c ,代入椭圆方程,可求得| F 1 A |=| F 1 B |=   . 又| F 1 F 2 |=2 c ,∠ F 1 F 2 A =30 ° , ∴   =   × 2 c ①. 又   =   × 2 c ×   =4   ②, a 2 = b 2 + c 2 ③, 由①②③解得 a 2 =9, b 2 =6, c 2 =3, ∴椭圆 C 的方程为   +   =1. 考点二　椭圆的几何性质 1. (2018安徽宣城二模,7)已知椭圆   +   =1( a > b >0)的左顶点为 M ,上顶点为 N ,右焦点为 F ,若   ·   =0,则椭圆的离心率为   (　　) A.   　    B.   　    C.   　    D.   答案    D　 由题意知, M (- a ,0), N (0, b ), F ( c ,0),∴   =(- a ,- b ),   =( c ,- b ).∵   ·   =0,∴- ac + b 2 =0, 即 b 2 = ac .又知 b 2 = a 2 - c 2 ,∴ a 2 - c 2 = ac .∴ e 2 + e -1=0,解得 e =   或 e =   (舍).∴椭圆的离心率为   ,故选D. 2. (2018豫南九校3月联考,9)已知两定点 A (-1,0)和 B (1,0),动点 P ( x , y )在直线 l : y = x +3上移动,椭圆 C 以 A , B 为焦点且经过点 P ,则椭圆 C 的离心率的最大值为   (　　) A.   　    B.   　    C.   　    D.   答案    A 　不妨设椭圆方程为   +   =1( a >1), 与直线 l 的方程联立得   消去 y 得(2 a 2 -1) x 2 +6 a 2 x +10 a 2 - a 4 =0, 由题意易知 Δ =36 a 4 -4(2 a 2 -1)(10 a 2 - a 4 ) ≥ 0, 解得 a ≥   , 所以 e =   =   ≤   , 所以 e 的最大值为   .故选A. 3. (2016江西五市八校二模,4)已知正数 m 是2和8的等比中项,则圆锥曲线 x 2 +   =1的焦点坐标为   (　　) A.( ±   ,0)　     B.(0, ±   ) C.( ±   ,0)或( ±   ,0)　    D.(0, ±   )或( ±   ,0) 答案    B　 因为正数 m 是2和8的等比中项,所以 m 2 =16,则 m =4,所以圆锥曲线 x 2 +   =1即为椭圆 x 2 +   =1,易知其焦点坐标为(0, ±   ),故选B. 4. (2017湖南百校联盟4月联考,10)已知椭圆   +   =1( a > b >0)的右顶点和上顶点分别为 A 、 B , 左焦点为 F .以原点 O 为圆心的圆与直线 BF 相切,且该圆与 y 轴的正半轴交于点 C ,过点 C 的直线 交椭圆于 M 、 N 两点.若四边形 FAMN 是平行四边形,则该椭圆的离心率为   (　　) A.   　    B.   　    C.   　    D.   答案    A 　∵圆 O 与直线 BF 相切,∴圆 O 的半径为   ,即 OC =   ,∵四边形 FAMN 是平行四边形, ∴点 M 的坐标为   ,代入椭圆方程得   +   =1,∴5 e 2 +2 e -3=0,又0< e <1,∴ e =   .故 选A. 5. (2018湖南雅礼中学4月月考,14)已知 F 1 、 F 2 分别是椭圆   +   =1的左、右焦点,动点 P 在椭 圆上,则| PF 1 |·| PF 2 |的最大值是 　　　     . 答案 　25 解析　 由椭圆方程可知 F 1 (-4,0), F 2 (4,0),设 P ( x 0 , y 0 ),则   +   =1,∴   =9   , 又| PF 1 |=   ,| PF 2 |=   , ∴| PF 1 |·| PF 2 | =   ·   =   ·   =   , 又∵ x 0 ∈[-5,5],∴   ∈[0,25],∴| PF 1 |·| PF 2 |=25-     ∈[9,25],∴| PF 1 |·| PF 2 |的最大值为25. 一题多解　 由椭圆的方程知 a =5, b =3,由椭圆的定义知| PF 1 |+| PF 2 |=10,∴| PF 1 |·| PF 2 | ≤   =5 2 =25,当且仅当| PF 1 |=| PF 2 |时等号成立.∴| PF 1 |·| PF 2 |的最大值为25. B组  2016—2018年高考模拟·综合题组 (时间:25分钟　　分值:40分) 一、选择题(每题5分,共30分) 1. (2018湖南师大附中4月模拟,10)设椭圆 C :   +   =1( a > b >0)的右焦点为 F ,椭圆 C 上的两点 A 、 B 关于原点对称,且满足   ·   =0,| FB | ≤ | FA | ≤ 2| FB |,则椭圆 C 的离心率的取值范围是   (　　) A.   　    B.   　    C.   　    D.[   -1,1) 答案    A　 设椭圆左焦点为 F ',连接 AF '、 BF '.由椭圆的对称性可知,四边形 AFBF '为平行四边 形,又   ·   =0,即 FA ⊥ FB ,故平行四边形 AFBF '为矩形,所以| AB |=| FF '|=2 c . 设| AF '|= n ,| AF |= m ,则在直角三角形 AF ' F 中 m + n =2 a , m 2 + n 2 =4 c 2 ,① 得 mn =2 b 2 ,② ① ÷ ②得   +   =   , 令   = t ,得 t +   =   . 又由| FB | ≤ | FA | ≤ 2| FB |得1 ≤   ≤ 2, 则   = t ∈[1,2],∴ t +   =   ∈   , 又   =   =   ,则可得   ≤ e ≤   ,即离心率的取值范围是   .故选A. 解题关键 　根据题意构造关于离心率 e 的不等式是求解本题的关键.在解决椭圆有关问题时注 意定义的运用. 思路分析 　设出椭圆左焦点 F ',由对称性知四边形 AFBF '为平行四边形,由   ·   =0,知该平行 四边形为矩形,设| AF '|= n ,| AF |= m .由椭圆定义及勾股定理得 mn =2 b 2 ,进而由 m 2 + n 2 =4 c 2 得   +   =   .再由| FB | ≤ | FA | ≤ 2| FB |得   的范围,从而利用相应函数的性质得出离心率的取值范围. 2. (2018湖南湘东五校联考,11)已知椭圆   +   =1( a > b >0)的左、右焦点分别为 F 1 、 F 2 , P 是椭圆 上一点,△ PF 1 F 2 是以 F 2 P 为底边的等腰三角形,且60 ° <∠ PF 1 F 2 <120 ° ,则该椭圆的离心率的取值 范围是   (　　) A.   　    B.   C.   　    D.   答案    B 　由题意可得,| PF 2 | 2 =| F 1 F 2 | 2 +| PF 1 | 2 -2| F 1 F 2 |·| PF 1 |cos∠ PF 1 F 2 =4 c 2 +4 c 2 -2·2 c ·2 c ·cos∠ PF 1 F 2 , 即| PF 2 |=2   c ·   ,所以 a =   = c +   c ·   ,又60 ° <∠ PF 1 F 2 <120 ° , ∴-   b >0)的左、右焦点,若椭圆 C 上 存在点 P 使∠ F 1 PF 2 为钝角,则椭圆 C 的离心率的取值范围是   (　　) A.   　    B.   　    C.   　    D.   答案    A 　设 P ( x 0 , y 0 ), F 1 (- c ,0), F 2 ( c ,0),由题易知| x 0 |< a ,因为存在点 P ,使∠ F 1 PF 2 为钝角,所以   ·   <0有解,即 c 2 >   +   有解,即 c 2 >(   +   ) min ,又   = b 2 -     , b 2 + c 2 = a 2 ,   < a 2 ,故   +   = b 2 +     ∈ [ b 2 , a 2 ),所以(   +   ) min = b 2 ,故 c 2 > b 2 ,所以 e 2 =   >   ,又0< e <1,∴   < e <1,故椭圆 C 的离心率的取值范 围是   ,故选A. 解题关键　 本题考查了平面向量的数量积在解题中的应用,体现了化归与转化思想,解答此题 的关键在于把存在点 P 使∠ F 1 PF 2 为钝角转化为   与   的数量积小于0有解. 一题多解　 如图,椭圆上存在点 P 使∠ F 1 PF 2 为钝角 ⇔ 以原点 O 为圆心, c 为半径的圆与椭圆有四 个不同的交点 ⇔ b < c ,由 b < c ,得 a 2 - c 2 < c 2 ,即 a 2 <2 c 2 ,即 e 2 <   ,又0< e <1,∴   < e <1.故椭圆 C 的离心率 的取值范围是   ,故选A.   5. (2017河南4月质检,11)已知椭圆 C :   +   =1( a > b >0)的右焦点为 F 2 , O 为坐标原点, M 为 y 轴上一 点,点 A 是直线 MF 2 与椭圆 C 的一个交点,且| OA |=| OF 2 |=2| OM |,则椭圆 C 的离心率为   (　　) A.   　    B.   　    C.   　    D.   答案    D     解法一:∵| OA |=| OF 2 |=2| OM |,则 M 在椭圆 C 的短轴上,设椭圆 C 的左焦点为 F 1 ,连接 AF 1 , ∵| OA |=| OF 2 |,∴| OA |=   | F 1 F 2 |,∴ AF 1 ⊥ AF 2 ,从而△ AF 1 F 2 ∽△ OMF 2 ,∴   =   =   ,又| AF 1 | 2 +| AF 2 | 2 =(2 c ) 2 ,∴| AF 1 |=   c ,| AF 2 |=   c ,又∵| AF 1 |+| AF 2 |=2 a ,∴   c =2 a ⇒   =   .故选D. 解法二:∵| OA |=| OF 2 |=2| OM |,∴ M 在椭圆 C 的短轴上,在Rt△ MOF 2 中,tan∠ MF 2 O =   =   ,设椭 圆 C 的左焦点为 F 1 ,连接 AF 1 ,∵| OA |=| OF 2 |,∴| OA |=   | F 1 F 2 |,∴ AF 1 ⊥ AF 2 ,∴tan∠ AF 2 F 1 =   =   , 设| AF 1 |= x ( x >0),则| AF 2 |=2 x ,所以| F 1 F 2 |=   x ,∴ e =   =   =   =   ,故选D. 6. (2016福建厦门一模,11)已知椭圆   +   =1的右焦点为 F , P 是椭圆上一点,点 A (0,2   ),当△ APF 的周长最大时,△ APF 的面积等于   (　　) A.   　    B.   　    C.   　    D.   答案    B 　由椭圆   +   =1知 a =3, b =   , c =   =2,在Rt△ AOF 中,| OF |=2,| OA |=2   ,则| AF |= 4.设椭圆的左焦点为 F 1 ,则△ APF 的周长为| AF |+| AP |+| PF |=| AF |+| AP |+2 a -| PF 1 |=4+6+| PA |-| PF 1 | ≤ 10+| AF 1 |(当且仅当 P 在线段 AF 1 的延长线上时取“=”).下面求当△ APF 周长最大时 P 的纵坐标: 易知 AF 1 的方程为   +   =1,与椭圆的方程5 x 2 +9 y 2 -45=0联立并整理得32 y 2 -20   y -75=0,解得 y P =-   (正值舍去).则△ APF 的周长最大时, S △ APF =   | F 1 F |·| y A - y P |=   × 4 ×   =   .故选B. 解题关键　 巧妙利用椭圆的定义及三角形的三边关系探求出△ APF 周长最大时点 P 位置是解 题的关键. 二、填空题(每题5分,共10分) 7. (2018山东烟台二模,15)已知 F (2,0)为椭圆   +   =1( a > b >0)的右焦点,过 F 且垂直于 x 轴的弦 长为6,若 A (-2,   ),点 M 为椭圆上任一点,则| MF |+| MA |的最大值为 　　　     . 答案 　8+   解析 　设椭圆的左焦点为 F ', 由椭圆的右焦点为 F (2,0),得 c =2,又过 F 且垂直于 x 轴的弦长为6,即   =6, 则   =   =3,解得 a =4, 所以| MF |+| MA |=8-| MF '|+| MA |=8+| MA |-| MF '|, 当 M , A , F '三点共线时,| MA |-| MF '|取得最大值,(| MA |-| MF '|) max =| AF '|=   , 所以| MF |+| MA |的最大值为8+   . 思路分析 　设出椭圆左焦点 F ',利用椭圆的定义将求| MF |+| MA |的最大值转化为求8+| MA |-| MF '| 的最大值,进而利用三点共线求解. 8 .(2018广东惠州三调,16)设 A 、 B 为椭圆   +   =1( a > b >0)的左、右顶点,若在椭圆上存在异于 A , B 的点 P ,使得   ·   =0,其中 O 为坐标原点,则椭圆的离心率 e 的取值范围是 　　　     . 答案        解析 　由题意知 A (- a ,0), B ( a ,0),设 P ( x , y ),则   =(- x ,- y ),   =( a - x ,- y ),又   ·   =0,∴( a - x )(- x )+ y 2 =0, 得 y 2 = ax - x 2 >0,∴0< x < a .将 y 2 = ax - x 2 代入   +   =1,整理得( b 2 - a 2 ) x 2 + a 3 x - a 2 b 2 =0,由题意知该方程在 (0, a )上有解. 设 f ( x )=( b 2 - a 2 ) x 2 + a 3 x - a 2 b 2 ,∵ f (0)=- a 2 b 2 <0, f ( a )=0, ∴只需   解得 a 2 >2 b 2 , 又 b 2 = a 2 - c 2 ,∴   >   ,又0< e <1,∴   < e <1. 解题关键 　求出点 P 的轨迹方程,并将问题转化为一元二次方程在一区间上有解的问题是解 题的关键.