空间中直线与直线之间的位置关系3 6页

‎ ‎ ‎2.1.2空间中直线与直线之间的位置关系 ‎（第1课时）‎ 一、教学目标：‎ ‎（1）了解空间中两条直线的位置关系，并能判断直线与直线之间的位置关系；‎ ‎（2）理解异面直线的概念、画法，培养学生的空间想象能力；‎ ‎（3）理解并掌握公理4，并能运用它证明简单的几何问题。‎ 二、教学重、难点：‎ ‎1．重点: （1）空间中两条直线的位置关系的判定；‎ ‎（2）理解并掌握公理4。‎ ‎2．难点: 理解异面直线的概念、画法。‎ 三、教具准备 ‎ 多媒体课件 长方体模型 自制的空间四边形模型 四、教学过程：‎ ‎（一）复习引入 ‎ 1 前面我们已学习了平面的概念及其基本性质。‎ 回顾一下，怎样确定一个平面呢？‎ ‎ （ 公理3及其三个推论 ）‎ ‎2 在一个平面内，两直线有哪几种位置关系呢？在空间中呢？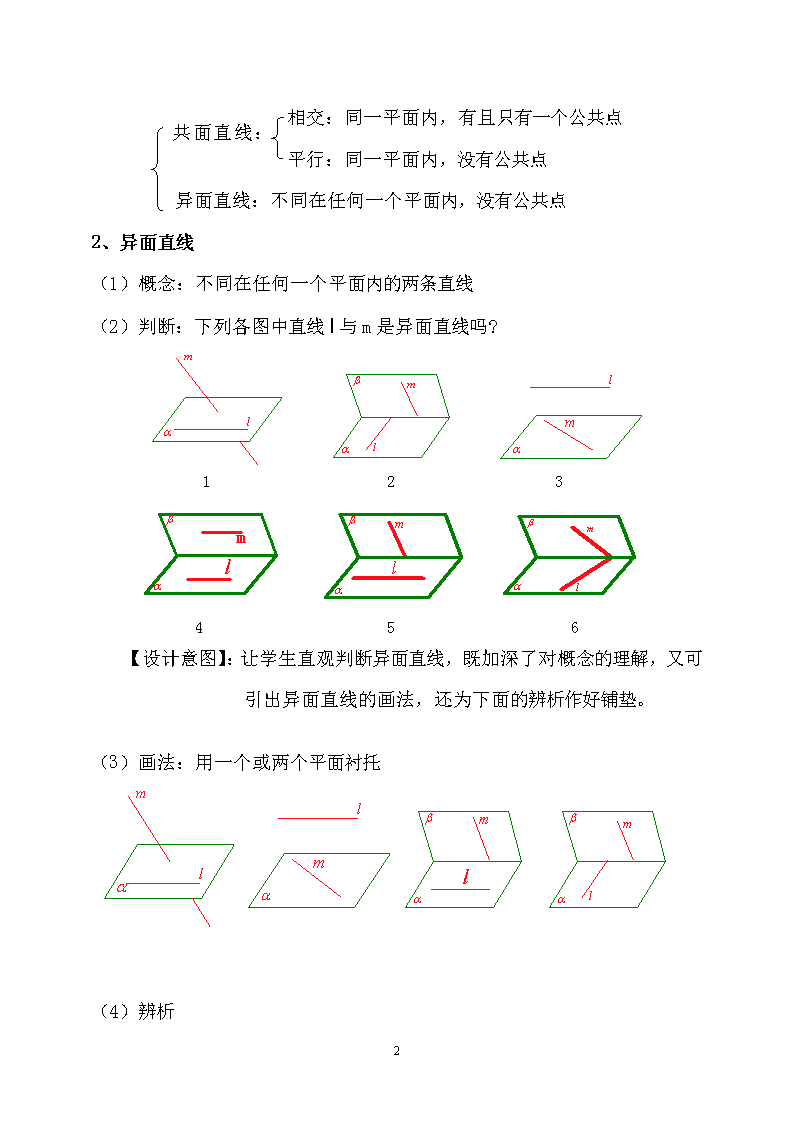‎ ‎（二）新课推进 ‎1、空间中两条直线的位置关系 以学生身边的实例引出空间两条直线位置关系问题 6‎ ‎ ‎ 共面直线：直线：‎ 相交：同一平面内，有且只有一个公共点 ‎ 平行：同一平面内，没有公共点 异面直线：不同在任何一个平面内，没有公共点 ‎2、异面直线 ‎（1）概念：不同在任何一个平面内的两条直线 ‎（2）判断：下列各图中直线l与m是异面直线吗?‎ ‎ 1 2 3‎ ‎ 4 5 6‎ ‎【设计意图】：让学生直观判断异面直线，既加深了对概念的理解，又可引出异面直线的画法，还为下面的辨析作好铺垫。‎ ‎（3）画法：用一个或两个平面衬托 ‎ ‎ ‎（4）辨析 6‎ ‎ ‎ ‎①、空间中没有公共点的两条直线是异面直线 ‎②、分别在两个不同平面内的两条直线是异面直线 ‎③、不同在某一平面内的两条直线是异面直线 ‎④、平面内的一条直线和平面外的一条直线是异面直线 ‎ ⑤、既不相交，又不平行的两条直线是异面直线 ‎ ‎（以上面（2）判断中的图6做反例）‎ ‎（5）结合实例小结判断异面直线的关键 ‎ ① 例1：如图2.1.2-1，在正方体中,‎ 哪些棱所在的直线与成异面直线?‎ ‎ 图2.1.2-1 ‎ ‎ ‎ ‎② 合作探究 如右图所示是一个正方体的展开图，如果将它还原成正方体，那么AB、CD、EF、GH这四条线段所在的直线是异面直线的有几对？‎ ‎ （用计算机演示还原成正方体，再让学生观察）‎ ‎【设计意图】：让学生根据异面直线的定义判断在几何体上的具有异面直线位置关系的两条直线.培养学生的空间想象能力,加深对异面直线概念的理解.‎ ‎③判断异面直线的关键：既不相交，又不平行 ‎3．公理4的教学 6‎ ‎ ‎ ‎⑴．思考：在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线平行。空间中,如果两条直线都与第三条直线平行,是否也有类似的规律?‎ 观察：如图2.1.2-2,长方体中,‎ AA1∥, AA1∥，那么与平行吗?‎ ‎【设计意图】：以长方体为载体,通过类比、观察引入 公理4：平行同一条直线的两直线互相平行.‎ 培养学生的总结归纳能力. 图2.1.2-2⑵．再联系其他相应实例（圆柱的母线与轴所在直线）归纳出公理4‎ 公理4：平行于同一条直线的两条直线互相平行。‎ 符号表示为：设a、b、c是三条直线 ‎=>a∥c a∥b b∥c 注：公理4实质上是说平行具有传递性，在平面、空间此性质都适用；‎ 公理4作用：判断空间两条直线平行的依据。‎ ‎⑶．讲解例2，让学生掌握公理4的运用 例2：如图在空间四边形ABCD中， ‎ E、F、G、H分别是AB、BC、CD、DA的中点。‎ ‎ 求证：四边形EFGH是平行四边形。 ‎ ‎（考虑到学生第一次接触空间四边形，先结自制模型简单介绍什么叫空间四边形，再分析如何证明）‎ 分析：如何判定一个四边形是平行四边形？‎ 6‎ ‎ ‎ ‎ 怎样证明EH∥ FG？证明关键是什么？‎ 证明：如图,连结BD．‎ ‎ ∵E、H 分别是AB、AD的中点 ‎ ‎ ∴EH是△ABD的中位线 ‎ ∴ EH∥ BD, ‎ 同理, FG∥ BD, ‎ ‎ ∴ EH∥ FG,且EH=FG ‎ ∴四边形EFGH是平行四边形。‎ 提问：有没有其它证明方法呢？（EF∥ HG,且EF=HG）‎ 变式练习：‎ ‎(1)在例2中, 如果再加上条件,那么四边形是什么图形?‎ ‎(2) 把条件改为: E、H分别是边AB、AD的中点，F、G分别是边CB、CD上的点，且 则四边形是什么图形?为什么?‎ ‎（先用课件进行动态演示，让学生观察猜想，再让学生尝试证明）‎ ‎【设计意图】：让学生掌握运用公理4证明简单几何问题的思路：将空间平行问题转化为平面内的平行问题。‎ ‎（三）练习 ‎1．设直线a、b分别是长方体相邻两个面的对角线所在的直线，则a、b的位置关系是 变式：若去掉“相邻”两字，那么答案又是什么？‎ ‎（先让学生自行判断，再借助长方体模型加以说明）‎ ‎2．如图2.1.2-3，在长方体中，‎ 6‎ ‎ ‎ ‎（1）若E、F分别是AB、BC的中点，则EF和A1C1的位置关系是 ‎（2）若E是AB的三等分点，F是AB、BC的中点，‎ 则EF和A1C1的位置关系是 ‎ （1） （2）‎ 图2.1.2-3‎ ‎（四）小结 ‎（1）空间中两直线有何位置关系？（平行、相交、异面）‎ ‎（2）怎样判断两直线是异面直线？（判断关键：既不平行又不相交）‎ ‎（3）什么是平行公理?它的作用是什么?‎ ‎ （平行同一条直线的两条直线互相平行 ‎ 作用：判断两直线平行 ‎ 它将空间平行问题转化为平面内的平行问题）‎ ‎（五）作业 (1) ‎ P56习题2.1A组第6题 (2) ‎ 如图2.1.2-4,在正方体中,与对角线成异面直线的棱共有几条? ‎ ‎ 图2.1.2-4‎ 6‎