高考文科数学复习备课课件：第二节　直线的交点与距离公式 31页

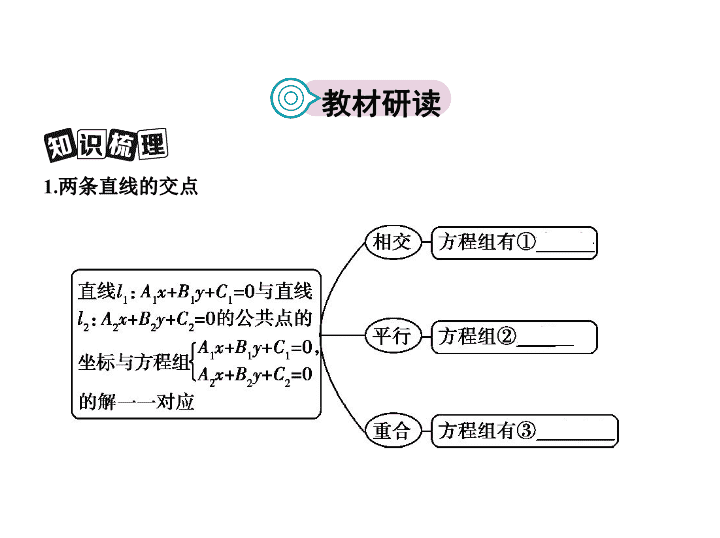
文数 课标版 第二节　直线的交点与距离公式 1.两条直线的交点 教材研读 2.三种距离 点 P 1 ( x 1 , y 1 ), P 2 ( x 2 , y 2 )之间的距离 | P 1 P 2 |=④             点 P 0 ( x 0 , y 0 )到直线 l : Ax + By + C =0的距离 d =⑤             两条平行直线 Ax + By + C 1 =0与 Ax + By + C 2 =0间的距离 d =⑥             判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)点 P ( x 0 , y 0 )到直线 y = kx + b 的距离为   .   ( × ) (2)直线外一点与直线上一点的距离的最小值就是点到直线的距离.   (√) (3)若点 A , B 关于直线 l : y = kx + b ( k ≠ 0)对称,则直线 AB 的斜率等于-   ,且线 段 AB 的中点在直线 l 上.   (√) 1.两条直线 l 1 :2 x + y -1=0和 l 2 : x -2 y +4=0的交点为   (　　) A.   　    B.   C.   　    D.   答案     B　解方程组   得   所以两直线的交点为   . 2.原点到直线 x +2 y -5=0的距离为   (　　) A.1　    B.   　　 C.2　    D.   答案     D　由相应距离公式易得 d =   =   . 3.已知直线 l 1 : x + y +1=0, l 2 : x + y -1=0,则 l 1 , l 2 之间的距离为   (　　) A.1　    B.   　    C.   　    D.2 答案     B　由题意可知 l 1 与 l 2 平行,故 l 1 与 l 2 之间的距离 d =   =   =   ,故选B. 4.若三条直线2 x +3 y +8=0, x - y -1=0和 x + by =0相交于一点,则 b = 　　　     . 答案 　-   解析 　由   解得   将其代入 x + by =0,得 b =-   . 5.已知坐标平面内两点 A ( x ,   - x )和 B   ,那么这两点之间距离的最 小值是 　　　     . 答案        解析 　由题意可得两点间的距离 d =   =   ≥   ,即最小值为   . 考点一　直线的交点 典例1 　(1)经过直线 l 1 : x + y +1=0与直线 l 2 : x - y +3=0的交点 P ,且与直线 l 3 :2 x - y +2=0垂直的直线 l 的方程是       . (2)已知三条直线 l 1 :4 x + y -4=0, l 2 : mx + y =0, l 3 :2 x -3 my -4=0,若它们不能围成三 角形,则 m 的取值构成的集合是 　　　     . 答案　 (1) x +2 y =0　(2)   解析　 (1)解法一:由方程组   解得   即点 P (-2,1), 由题意知直线 l 的斜率存在,设直线 l 的方程为 y -1= k ( x +2), ∵ l 3 ⊥ l ,∴ k =-   , ∴直线 l 的方程为 y -1=-   ( x +2),即 x +2 y =0. 考点突破 解法二:因为直线 l 过直线 l 1 和 l 2 的交点, 所以可设直线 l 的方程为 x + y +1+ λ ( x - y +3)=0, 即(1+ λ ) x +(1- λ ) y +1+3 λ =0. 因为 l 与 l 3 垂直, 所以2(1+ λ )-(1- λ )=0,所以 λ =-   , 所以直线 l 的方程为   x +   y =0,即 x +2 y =0. (2)由已知易知 l 2 与 l 3 相交,且交点为   ,若 l 1 、 l 2 、 l 3 交于一 点,则易得 m =-1或   ;若 l 1 ∥ l 2 ,则 m =4;若 l 1 ∥ l 3 ,则 m =-   .综上可得, m =-1或   或4或-   . 1.两直线交点的求法 求两直线的交点坐标,就是解由两直线方程组成的方程组,以方程组的 解为点的坐标,即交点的坐标. 方法技巧 2.求过两直线交点的直线方程的方法 (1)求过两直线交点的直线方程,先解方程组求出两直线的交点坐标,再 结合其他条件写出直线方程. (2)利用直线系方程求解.经过两相交直线 A 1 x + B 1 y + C 1 =0和 A 2 x + B 2 y + C 2 =0 的交点的直线系方程为 A 1 x + B 1 y + C 1 + λ ( A 2 x + B 2 y + C 2 )=0(这个直线系不包 括直线 A 2 x + B 2 y + C 2 =0). 变式1-1　 若将本例(1)中的条件“垂直”改为“平行”,试求 l 的方程. 解析 　由方程组   解得   即点 P (-2,1). 设直线 l 的方程为 y -1= k ( x +2), 因为 l ∥ l 3 ,所以 k =2,故直线 l 的方程为 y -1=2( x +2),即2 x - y +5=0. 1-2 　当0< k <   时,直线 l 1 : kx - y = k -1与直线 l 2 : ky - x =2 k 的交点在   (　　) A.第一象限　    B.第二象限 C.第三象限　    D.第四象限 答案     B　由   得   又∵0< k <   , ∴ x =   <0, y =   >0, 故直线 l 1 : kx - y = k -1与直线 l 2 : ky - x =2 k 的交点在第二象限. 考点二　距离问题 典例2 　(1)若 P , Q 分别为直线3 x +4 y -12=0与6 x +8 y +5=0上任意一点,则| PQ |的最小值为   (　　) A.   　    B.   　    C.   　    D.   (2)已知 A (4,-3), B (2,-1)和直线 l :4 x +3 y -2=0,在坐标平面内存在一点 P ,使 | PA |=| PB |,且点 P 到直线 l 的距离为2,则点 P 坐标为 　　　　　　　　     . 答案　 (1)C　(2)(1,-4)或   解析 　(1)因为   =   ≠   ,所以两直线平行, 由题意可知| PQ |的最小值为这两条平行直线间的距离,即   =   , 所以| PQ |的最小值为   . (2)设点 P 的坐标为( a , b ),∵ A (4,-3), B (2,-1), ∴线段 AB 的中点 M 的坐标为(3,-2), 而 AB 的斜率 k AB =   =-1, ∴线段 AB 的垂直平分线方程为 y +2= x -3, 即 x - y -5=0. ∵点 P ( a , b )在直线 x - y -5=0上, ∴ a - b -5=0.   ① 又点 P ( a , b )到直线 l :4 x +3 y -2=0的距离为2, ∴   =2, 即4 a +3 b -2= ± 10,   ② 由①②联立可得   或   ∴点 P 的坐标为(1,-4)或   . 易错警示 (1)点 P ( x 0 , y 0 )到直线 x = a 的距离 d =| x 0 - a |,到直线 y = b 的距离 d =| y 0 - b |; (2)在运用两平行线间的距离公式时要把两直线方程中 x , y 的系数化为 相等. 2-1 　已知直线3 x +4 y -3=0与直线6 x + my +14=0平行,则它们之间的距离是   (　　) A.   　    B.   　    C.8　    D.2 答案     D　∵   =   ≠   ,∴ m =8,直线6 x + my +14=0可化为3 x +4 y +7=0,两 平行线之间的距离 d =   =2. 2-2　 已知 P 点坐标为(2,-1). (1)求过 P 点且与原点距离为2的直线 l 的方程; (2)求过 P 点且与原点距离最大的直线 l 的方程,并求出最大距离; (3)是否存在过 P 点且与原点距离为6的直线?若存在,求出方程;若不存 在,请说明理由. 解析 　(1)过 P 点的直线 l 与原点距离为2,又 P 点坐标为(2,-1),可见,过 P (2,- 1)且垂直于 x 轴的直线满足条件, 此时 l 的斜率不存在,其方程为 x =2. 若斜率存在,则设 l 的方程为 y +1= k ( x -2), 即 kx - y -2 k -1=0. 则   =2, 解得 k =   . 此时 l 的方程为3 x -4 y -10=0. 综上,直线 l 的方程为 x =2或3 x -4 y -10=0. (2)由题意可知过 P 点且与原点距离最大的直线 l 是过 P 点且与 PO ( O 为坐 标原点)垂直的直线,由 l ⊥ OP ,得 k l k OP =-1, 所以 k l =-   =2. 由点斜式得直线 l 的方程为 y +1=2( x -2),即2 x - y -5=0. 所以2 x - y -5=0是过 P 点且与原点距离最大的直线的方程,最大距离为   =   . (3)不存在.由(2)可知,过 P 点不存在与原点距离超过   的直线,因此不存 在过 P 点且与原点距离为6的直线. 考点三　对称问题 命题角度一　点关于点的对称 典例3 　过点 P (0,1)作直线 l 使它被直线 l 1 :2 x + y -8=0和 l 2 : x -3 y +10=0截得的 线段被点 P 平分,求直线 l 的方程. 解析　 设 l 1 与 l 的交点为 A ( a ,8-2 a ), 则由题意知,点 A 关于点 P 的对称点 B (- a ,2 a -6)在 l 2 上, 将其代入 l 2 的方程,得- a -3(2 a -6)+10=0, 解得 a =4,则 A (4,0),又 P (0,1), 所以由两点式可得直线 l 的方程为 x +4 y -4=0. 典例4 　求点 A (-1,-2)关于直线 l :2 x -3 y +1=0的对称点 A '的坐标. 解析　 设 A '( x , y ),则由已知得   解得   ∴ A '   . 命题角度二　点关于线的对称 典例5 　求直线 l :2 x -3 y +1=0关于点 A (-1,-2)对称的直线 l '的方程. 解析 　设 P ( x , y )为 l '上任意一点, 则 P ( x , y )关于点 A (-1,-2)的对称点为 P '(-2- x ,-4- y ), ∵点 P '在直线 l 上,∴2(-2- x )-3(-4- y )+1=0, 即2 x -3 y -9=0. 则直线 l '的方程为2 x -3 y -9=0. 命题角度三　线关于点的对称 典例6 　求直线 m :3 x -2 y -6=0关于直线 l :2 x -3 y +1=0的对称直线 m '的方程. 解析　 在直线 m 上任取一点,如点 M (2,0),则点 M (2,0)关于直线 l 的对称点 M '必在直线 m '上. 设点 M 的对称点 M '的坐标为( a , b ),则   解得   故点 M '的坐标为   . 设直线 m 与直线 l 的交点为 N , 由   解得   则 N (4,3). 命题角度四　线关于线的对称 ∴由两点式可得直线 m '的方程为9 x -46 y +102=0. 典例7 　在等腰直角三角形 ABC 中, AB = AC =4,点 P 是边 AB 上异于 A , B 的 一点.光线从点 P 出发,经 BC , CA 反射后又回到点 P (如图).若光线 QR 经过 △ ABC 的重心,则 AP 等于   (　　)   A.2　    B.1　    C.   　    D.   命题角度五　对称问题的应用 答案     D 解析 　以 AB 所在直线为 x 轴, AC 所在直线为 y 轴建立如图所示的坐标系, 由题意可知 B (4,0), C (0,4), A (0,0),则直线 BC 的方程为 x + y -4=0. 设 P ( t ,0)(0< t <4),由对称知识可得点 P 关于直线 BC 的对称点 P 1 的坐标为 (4,4- t ),点 P 关于 y 轴的对称点 P 2 的坐标为(- t ,0),根据反射定理可知直线 P 1 P 2 就是光线 RQ 所在直线.由 P 1 、 P 2 两点坐标可得直线 P 1 P 2 的方程为 y =   ·( x + t ),设△ ABC 的重心为 G ,易知 G   .因为重心 G   在光线 RQ 上,所以   =     ,即3 t 2 -4 t =0,解得 t =0或 t =   , 因为0< t <4,所以 t =   , 即 AP =   ,故选D. 1.中心对称问题的两个类型及求解方法 (1)点关于点对称:若点 M ( x 1 , y 1 )及 N ( x , y )关于 P ( a , b )对称,则由中点坐标公 式得   进而求解. (2)直线关于点的对称,主要求解方法如下: ①在已知直线上取两点,利用中点坐标公式求出它们关于已知点对称的 两点坐标,再由两点式求出直线方程; ②求出一个对称点,再利用两对称直线平行,由点斜式得到所求直线方 程. 方法技巧 2.轴对称问题的两个类型及求解方法 (1)点关于直线的对称: 若两点 P 1 ( x 1 , y 1 )与 P 2 ( x 2 , y 2 )关于直线 l : Ax + By + C =0对称,由方程组   可得到点 P 1 关于 l 对称的点 P 2 的坐标( x 2 , y 2 )(其 中 B ≠ 0, x 1 ≠ x 2 ). (2)直线关于直线对称: ①若直线与对称轴平行,则在直线上取一点,求出该点关于轴的对称点, 然后用点斜式求解; ②若直线与对称轴相交,则先求出交点,然后再取直线上一点,求该点关 于轴的对称点,最后由两点式求解. 3-1　 一条光线经过点 P (2,3)射在直线 l : x + y +1=0上,反射后经过点 Q (1,1), 求: (1)入射光线所在直线的方程; (2)这条光线从 P 到 Q 所经路线的长度. 解析 　(1)设点 Q '( x ', y ')为 Q 关于直线 l 的对称点, QQ '交 l 于点 M ,∵ k l =-1,∴ k QQ ' =1, ∴ QQ '所在直线的方程为 y -1=1·( x -1),即 x - y =0. 由   解得   ∴交点 M   ,∴   解得   ∴ Q '(-2,-2). 设入射光线与 l 交于点 N ,则 P , N , Q '三点共线, 又 P (2,3), Q '(-2,-2), 故入射光线所在直线的方程为   =   , 即5 x -4 y +2=0.   (2)| PN |+| NQ |=| PN |+| NQ '|=| PQ '| =   =   , 即这条光线从 P 到 Q 所经路线的长度为   .