2013年全国统一高考数学试卷（理科）（新课标ⅰ） 30页

‎2013年全国统一高考数学试卷（理科）（新课标Ⅰ）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的.‎ ‎1．（5分）已知集合A={x|x2﹣2x＞0}，B={x|﹣＜x＜}，则（　　）‎ A．A∩B=∅ B．A∪B=R C．B⊆A D．A⊆B ‎2．（5分）若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（　　）‎ A．﹣4 B． C．4 D．‎ ‎3．（5分）为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是（　　）‎ A．简单的随机抽样 B．按性别分层抽样 C．按学段分层抽样 D．系统抽样 ‎4．（5分）已知双曲线C：（a＞0，b＞0）的离心率为，则C的渐近线方程为（　　）‎ A．y= B．y= C．y=±x D．y=‎ ‎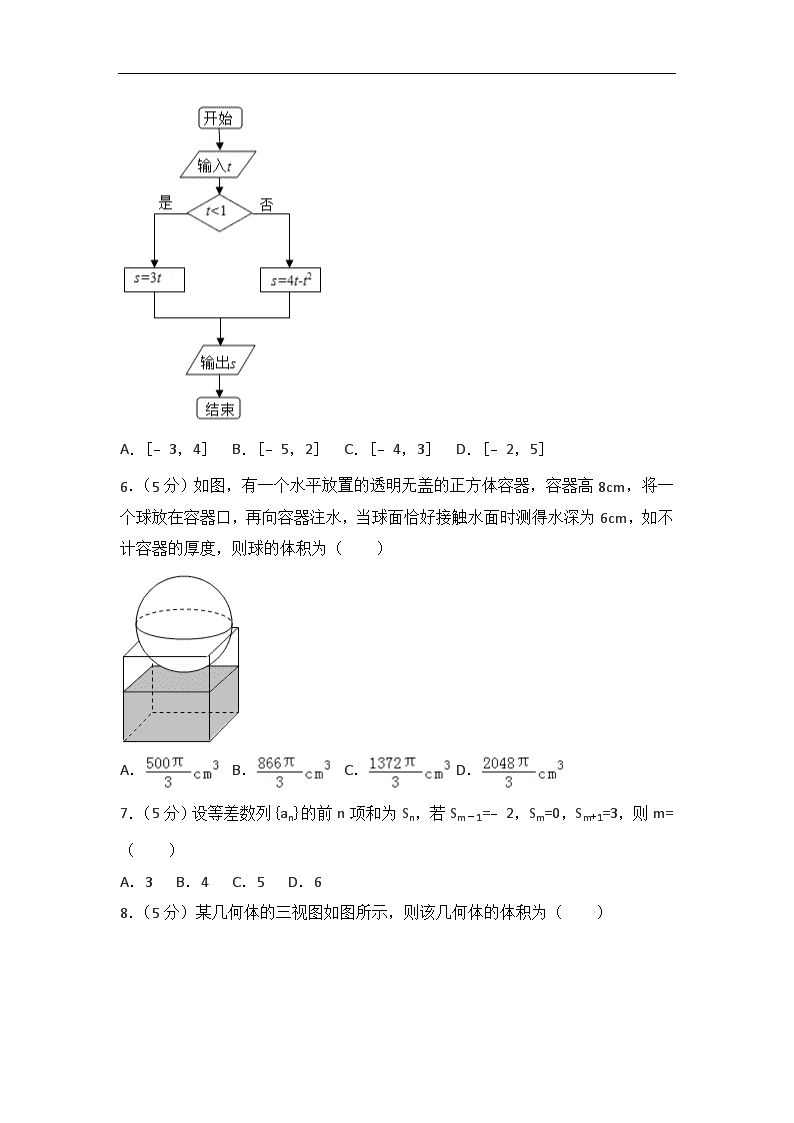5．（5分）执行程序框图，如果输入的t∈[﹣1，3]，则输出的s属于（　　）‎ A．[﹣3，4] B．[﹣5，2] C．[﹣4，3] D．[﹣2，5]‎ ‎6．（5分）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为（　　）‎ A． B． C． D．‎ ‎7．（5分）设等差数列{an}的前n项和为Sn，若Sm﹣1=﹣2，Sm=0，Sm+1=3，则m=（　　）‎ A．3 B．4 C．5 D．6‎ ‎8．（5分）某几何体的三视图如图所示，则该几何体的体积为（　　）‎ A．16+8π B．8+8π C．16+16π D．8+16π ‎9．（5分）设m为正整数，（x+y）2m展开式的二项式系数的最大值为a，（x+y）2m+1展开式的二项式系数的最大值为b，若13a=7b，则m=（　　）‎ A．5 B．6 C．7 D．8‎ ‎10．（5分）已知椭圆E：的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（　　）‎ A． B．‎ C． D．‎ ‎11．（5分）已知函数f（x）=，若|f（x）|≥ax，则a的取值范围是（　　）‎ A．（﹣∞，0] B．（﹣∞，1] C．[﹣2，1] D．[﹣2，0]‎ ‎12．（5分）设△AnBnCn的三边长分别为an，bn，cn，△AnBnCn的面积为Sn，n=1，2，3…若b1＞c1，b1+c1=2a1，an+1=an，，，则（　　）‎ A．{Sn}为递减数列 B．{Sn}为递增数列 C．{S2n﹣1}为递增数列，{S2n}为递减数列 D．{S2n﹣1}为递减数列，{S2n}为递增数列 ‎　‎ 二.填空题：本大题共4小题，每小题5分.‎ ‎13．（5分）已知两个单位向量，的夹角为60°，=t+（1﹣t）．若•=0，则t=　 　．‎ ‎14．（5分）若数列{an}的前n项和为Sn=an+，则数列{an}的通项公式是an=　 　．‎ ‎15．（5分）设当x=θ时，函数f（x）=sinx﹣2cosx取得最大值，则cosθ=　 　．‎ ‎16．（5分）若函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣2对称，则f（x）的最大值为　 　．‎ ‎　‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤.‎ ‎17．（12分）如图，在△ABC中，∠ABC=90°，AB=，BC=1，P为△ABC内一点，∠BPC=90°．‎ ‎（1）若PB=，求PA；‎ ‎（2）若∠APB=150°，求tan∠PBA．‎ ‎18．（12分）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．‎ ‎（Ⅰ）证明AB⊥A1C；‎ ‎（Ⅱ）若平面ABC⊥平面AA1B1B，AB=CB=2，求直线A1C与平面BB1C1C所成角的正弦值．‎ ‎19．（12分）一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n．如果n=3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n=4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的产品是优质品的概率都为，且各件产品是否为优质品相互独立．‎ ‎（Ⅰ）求这批产品通过检验的概率；‎ ‎（Ⅱ）已知每件产品检验费用为100元，凡抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X（单位：元），求X的分布列及数学期望．‎ ‎20．（12分）已知圆M：（x+1）2+y2=1，圆N：（x﹣1）2+y2=9，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C．‎ ‎（Ⅰ）求C的方程；‎ ‎（Ⅱ）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|．‎ ‎21．（12分）已知函数f（x）=x2+ax+b，g（x）=ex（cx+d），若曲线y=f（x）和曲线y=g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2．‎ ‎（Ⅰ）求a，b，c，d的值；‎ ‎（Ⅱ）若x≥﹣2时，f（x）≤kg（x），求k的取值范围．‎ ‎　‎ 四、请考生在第22、23、24题中任选一道作答，并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分，不涂，按本选考题的首题进行评分.‎ ‎22．（10分）（选修4﹣1：几何证明选讲）‎ 如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D．‎ ‎（Ⅰ）证明：DB=DC；‎ ‎（Ⅱ）设圆的半径为1，BC=，延长CE交AB于点F，求△BCF外接圆的半径．‎ ‎23．已知曲线C1的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ．‎ ‎（1）把C1的参数方程化为极坐标方程；‎ ‎（2）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）．‎ ‎24．已知函数f（x）=|2x﹣1|+|2x+a|，g（x）=x+3．‎ ‎（Ⅰ）当a=﹣2时，求不等式f（x）＜g（x）的解集；‎ ‎（Ⅱ）设a＞﹣1，且当x∈[﹣，]时，f（x）≤g（x），求a的取值范围．‎ ‎　‎ ‎2013年全国统一高考数学试卷（理科）（新课标Ⅰ）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的.‎ ‎1．（5分）已知集合A={x|x2﹣2x＞0}，B={x|﹣＜x＜}，则（　　）‎ A．A∩B=∅ B．A∪B=R C．B⊆A D．A⊆B ‎【分析】根据一元二次不等式的解法，求出集合A，再根据的定义求出A∩B和A∪B．‎ ‎【解答】解：∵集合A={x|x2﹣2x＞0}={x|x＞2或x＜0}，‎ ‎∴A∩B={x|2＜x＜或﹣＜x＜0}，A∪B=R，‎ 故选：B．‎ ‎【点评】本题考查一元二次不等式的解法，以及并集的定义，属于基础题．‎ ‎　‎ ‎2．（5分）若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（　　）‎ A．﹣4 B． C．4 D．‎ ‎【分析】由题意可得 z==，再利用两个复数代数形式的乘除法法则化简为 +i，由此可得z的虚部．‎ ‎【解答】解：∵复数z满足（3﹣4i）z=|4+3i|，∴z====+i，‎ 故z的虚部等于，‎ 故选：D．‎ ‎【点评】本题主要考查复数的基本概念，两个复数代数形式的乘除法法则的应用，属于基础题．‎ ‎　‎ ‎3．（5分）为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是（　　）‎ A．简单的随机抽样 B．按性别分层抽样 C．按学段分层抽样 D．系统抽样 ‎【分析】若总体由差异明显的几部分组成时，经常采用分层抽样的方法进行抽样．‎ ‎【解答】解：我们常用的抽样方法有：简单随机抽样、分层抽样和系统抽样，‎ 而事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．‎ 了解某地区中小学生的视力情况，按学段分层抽样，这种方式具有代表性，比较合理．‎ 故选：C．‎ ‎【点评】本小题考查抽样方法，主要考查抽样方法，属基本题．‎ ‎　‎ ‎4．（5分）已知双曲线C：（a＞0，b＞0）的离心率为，则C的渐近线方程为（　　）‎ A．y= B．y= C．y=±x D．y=‎ ‎【分析】由离心率和abc的关系可得b2=4a2，而渐近线方程为y=±x，代入可得答案．‎ ‎【解答】解：由双曲线C：（a＞0，b＞0），‎ 则离心率e===，即4b2=a2，‎ 故渐近线方程为y=±x=x，‎ 故选：D．‎ ‎【点评】本题考查双曲线的简单性质，涉及的渐近线方程，属基础题．‎ ‎　‎ ‎5．（5分）执行程序框图，如果输入的t∈[﹣1，3]，则输出的s属于（　　）‎ A．[﹣3，4] B．[﹣5，2] C．[﹣4，3] D．[﹣2，5]‎ ‎【分析】本题考查的知识点是程序框图，分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算一个分段函数的函数值，由条件为t＜1我们可得，分段函数的分类标准，由分支结构中是否两条分支上对应的语句行，我们易得函数的解析式．‎ ‎【解答】解：由判断框中的条件为t＜1，可得：‎ 函数分为两段，即t＜1与t≥1，‎ 又由满足条件时函数的解析式为：s=3t；‎ 不满足条件时，即t≥1时，函数的解析式为：s=4t﹣t2‎ 故分段函数的解析式为：s=，‎ 如果输入的t∈[﹣1，3]，画出此分段函数在t∈[﹣1，3]时的图象，‎ 则输出的s属于[﹣3，4]．‎ 故选：A．‎ ‎【点评】要求条件结构对应的函数解析式，要分如下几个步骤：①分析流程图的结构，分析条件结构是如何嵌套的，以确定函数所分的段数；②根据判断框中的条件，设置分类标准；③根据判断框的“是”与“否”分支对应的操作，分析函数各段的解析式；④对前面的分类进行总结，写出分段函数的解析式．‎ ‎　‎ ‎6．（5分）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为（　　）‎ A． B． C． D．‎ ‎【分析】设正方体上底面所在平面截球得小圆M，可得圆心M为正方体上底面正方形的中心．设球的半径为R，根据题意得球心到上底面的距离等于（R﹣2）cm，而圆M的半径为4，由球的截面圆性质建立关于R的方程并解出R=5，用球的体积公式即可算出该球的体积．‎ ‎【解答】解：设正方体上底面所在平面截球得小圆M，‎ 则圆心M为正方体上底面正方形的中心．如图．‎ 设球的半径为R，根据题意得球心到上底面的距离等于（R﹣2）cm，‎ 而圆M的半径为4，由球的截面圆性质，得R2=（R﹣2）2+42，‎ 解出R=5，‎ ‎∴根据球的体积公式，该球的体积V===．‎ 故选：A．‎ ‎【点评】本题给出球与正方体相切的问题，求球的体积，着重考查了正方体的性质、球的截面圆性质和球的体积公式等知识，属于中档题．‎ ‎　‎ ‎7．（5分）设等差数列{an}的前n项和为Sn，若Sm﹣1=﹣2，Sm=0，Sm+1=3，则m=（　　）‎ A．3 B．4 C．5 D．6‎ ‎【分析】由an与Sn的关系可求得am+1与am，进而得到公差d，由前n项和公式及Sm=0可求得a1，再由通项公式及am=2可得m值．‎ ‎【解答】解：am=Sm﹣Sm﹣1=2，am+1=Sm+1﹣Sm=3，‎ 所以公差d=am+1﹣am=1，‎ Sm==0，得a1=﹣2，‎ 所以am=﹣2+（m﹣1）•1=2，解得m=5，‎ 另解：等差数列{an}的前n项和为Sn，即有数列{}成等差数列，‎ 则，，成等差数列，‎ 可得2•=+，‎ 即有0=+，‎ 解得m=5．‎ 又一解：由等差数列的求和公式可得（m﹣1）（a1+am﹣1）=﹣2，‎ m（a1+am）=0，（m+1）（a1+am+1）=3，‎ 可得a1=﹣am，﹣2am+am+1+am+1=+=0，‎ 解得m=5．‎ 故选：C．‎ ‎【点评】本题考查等差数列的通项公式、前n项和公式及通项an与Sn的关系，考查学生的计算能力．‎ ‎　‎ ‎8．（5分）某几何体的三视图如图所示，则该几何体的体积为（　　）‎ A．16+8π B．8+8π C．16+16π D．8+16π ‎【分析】三视图复原的几何体是一个长方体与半个圆柱的组合体，依据三视图的数据，得出组合体长、宽、高，即可求出几何体的体积．‎ ‎【解答】解：三视图复原的几何体是一个长方体与半个圆柱的组合体，如图，其中长方体长、宽、高分别是：4，2，2，半个圆柱的底面半径为2，母线长为4．‎ ‎∴长方体的体积=4×2×2=16，‎ 半个圆柱的体积=×22×π×4=8π 所以这个几何体的体积是16+8π；‎ 故选：A．‎ ‎【点评】本题考查了几何体的三视图及直观图的画法，三视图与直观图的关系，柱体体积计算公式，空间想象能力 ‎　‎ ‎9．（5分）设m为正整数，（x+y）2m展开式的二项式系数的最大值为a，（x+y）2m+1展开式的二项式系数的最大值为b，若13a=7b，则m=（　　）‎ A．5 B．6 C．7 D．8‎ ‎【分析】根据二项式系数的性质求得a和b，再利用组合数的计算公式，解方程13a=7b求得m的值．‎ ‎【解答】解：∵m为正整数，由（x+y）2m展开式的二项式系数的最大值为a，以及二项式系数的性质可得a=，‎ 同理，由（x+y）2m+1展开式的二项式系数的最大值为b，可得b==．‎ 再由13a=7b，可得13=7，即 13×=7×，‎ 即 13=7×，即 13（m+1）=7（2m+1），解得m=6，‎ 故选：B．‎ ‎【点评】本题主要考查二项式系数的性质的应用，组合数的计算公式，属于中档题．‎ ‎　‎ ‎10．（5分）已知椭圆E：‎ 的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（　　）‎ A． B．‎ C． D．‎ ‎【分析】设A（x1，y1），B（x2，y2），代入椭圆方程得，利用“点差法”可得．利用中点坐标公式可得x1+x2=2，y1+y2=﹣2，利用斜率计算公式可得==．于是得到，化为a2=2b2，再利用c=3=，即可解得a2，b2．进而得到椭圆的方程．‎ ‎【解答】解：设A（x1，y1），B（x2，y2），‎ 代入椭圆方程得，‎ 相减得，‎ ‎∴．‎ ‎∵x1+x2=2，y1+y2=﹣2，==．‎ ‎∴，‎ 化为a2=2b2，又c=3=，解得a2=18，b2=9．‎ ‎∴椭圆E的方程为．‎ 故选：D．‎ ‎【点评】熟练掌握“点差法”和中点坐标公式、斜率的计算公式是解题的关键．‎ ‎　‎ ‎11．（5分）已知函数f（x）=，若|f（x）|≥ax，则a的取值范围是（　　）‎ A．（﹣∞，0] B．（﹣∞，1] C．[﹣2，1] D．[﹣2，0]‎ ‎【分析】由函数图象的变换，结合基本初等函数的图象可作出函数y=|f（x）|的图象，和函数y=ax的图象，由导数求切线斜率可得l的斜率，进而数形结合可得a的范围．‎ ‎【解答】解：由题意可作出函数y=|f（x）|的图象，和函数y=ax的图象，‎ 由图象可知：函数y=ax的图象为过原点的直线，当直线介于l和x轴之间符合题意，直线l为曲线的切线，且此时函数y=|f（x）|在第二象限的部分解析式为y=x2﹣2x，‎ 求其导数可得y′=2x﹣2，因为x≤0，故y′≤﹣2，故直线l的斜率为﹣2，‎ 故只需直线y=ax的斜率a介于﹣2与0之间即可，即a∈[﹣2，0]‎ 故选：D．‎ ‎【点评】‎ 本题考查其它不等式的解法，数形结合是解决问题的关键，属中档题．‎ ‎　‎ ‎12．（5分）设△AnBnCn的三边长分别为an，bn，cn，△AnBnCn的面积为Sn，n=1，2，3…若b1＞c1，b1+c1=2a1，an+1=an，，，则（　　）‎ A．{Sn}为递减数列 B．{Sn}为递增数列 C．{S2n﹣1}为递增数列，{S2n}为递减数列 D．{S2n﹣1}为递减数列，{S2n}为递增数列 ‎【分析】由an+1=an可知△AnBnCn的边BnCn为定值a1，由bn+1+cn+1﹣2a1=及b1+c1=2a1得bn+cn=2a1，则在△AnBnCn中边长BnCn=a1为定值，另两边AnCn、AnBn的长度之和bn+cn=2a1为定值，‎ 由此可知顶点An在以Bn、Cn为焦点的椭圆上，根据bn+1﹣cn+1=，得bn﹣cn=，可知n→+∞时bn→cn，据此可判断△AnBnCn的边BnCn的高hn随着n的增大而增大，再由三角形面积公式可得到答案．‎ ‎【解答】解：b1=2a1﹣c1且b1＞c1，∴2a1﹣c1＞c1，∴a1＞c1，‎ ‎∴b1﹣a1=2a1﹣c1﹣a1=a1﹣c1＞0，∴b1＞a1＞c1，‎ 又b1﹣c1＜a1，∴2a1﹣c1﹣c1＜a1，∴2c1＞a1，∴，‎ 由题意，+an，∴bn+1+cn+1﹣2an=（bn+cn﹣2an），‎ ‎∴bn+cn﹣2an=0，∴bn+cn=2an=2a1，∴bn+cn=2a1，‎ 由此可知顶点An在以Bn、Cn为焦点的椭圆上，‎ 又由题意，bn+1﹣cn+1=，∴=a1﹣bn，‎ ‎∴bn+1﹣a1=，∴bn﹣a1=，‎ ‎∴，cn=2a1﹣bn=，‎ ‎∴‎ ‎[][]‎ ‎=[﹣]单调递增（可证当n=1时＞0）‎ 故选：B．‎ ‎【点评】本题主要考查由数列递推式求数列通项、三角形面积海伦公式，综合考查学生分析解决问题的能力，有较高的思维抽象度，是本年度全国高考试题中的“亮点”之一．‎ ‎　‎ 二.填空题：本大题共4小题，每小题5分.‎ ‎13．（5分）已知两个单位向量，的夹角为60°，=t+（1﹣t）．若•=0，则t=　2　．‎ ‎【分析】由于•=0，对式子=t+（1﹣t）两边与作数量积可得=0，经过化简即可得出．‎ ‎【解答】解：∵，，∴=0，‎ ‎∴tcos60°+1﹣t=0，∴1=0，解得t=2．‎ 故答案为2．‎ ‎【点评】熟练掌握向量的数量积运算是解题的关键．‎ ‎　‎ ‎14．（5分）若数列{an}的前n项和为Sn=an+，则数列{an}的通项公式是an=　（﹣2）n﹣1　．‎ ‎【分析】把n=1代入已知式子可得数列的首项，由n≥2时，an=Sn﹣Sn﹣1，可得数列为等比数列，且公比为﹣2，代入等比数列的通项公式分段可得答案．‎ ‎【解答】解：当n=1时，a1=S1=，解得a1=1‎ 当n≥2时，an=Sn﹣Sn﹣1=（）﹣（）=，‎ 整理可得，即=﹣2，‎ 故数列{an}从第二项开始是以﹣2为首项，﹣2为公比的等比数列，‎ 故当n≥2时，an=（﹣2）n﹣1，‎ 经验证当n=1时，上式也适合，‎ 故答案为：（﹣2）n﹣1‎ ‎【点评】本题考查等比数列的通项公式，涉及等比数列的判定，属基础题．‎ ‎　‎ ‎15．（5分）设当x=θ时，函数f（x）=sinx﹣2cosx取得最大值，则cosθ=　﹣　．‎ ‎【分析】f（x）解析式提取，利用两角和与差的正弦函数公式化为一个角的正弦函数，由x=θ时，函数f（x）取得最大值，得到sinθ﹣2cosθ=，与sin2θ+cos2θ=1联立即可求出cosθ的值．‎ ‎【解答】解：f（x）=sinx﹣2cosx=（sinx﹣cosx）=sin（x﹣α）（其中cosα=，sinα=），‎ ‎∵x=θ时，函数f（x）取得最大值，‎ ‎∴sin（θ﹣α）=1，即sinθ﹣2cosθ=，‎ 又sin2θ+cos2θ=1，‎ 联立得（2cosθ+）2+cos2θ=1，解得cosθ=﹣．‎ 故答案为：﹣‎ ‎【点评】此题考查了两角和与差的正弦函数公式，同角三角函数间的基本关系，以及正弦函数的定义域与值域，熟练掌握公式是解本题的关键．‎ ‎　‎ ‎16．（5分）若函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣2对称，则f（x）的最大值为　16　．‎ ‎【分析】由题意得f（﹣1）=f（﹣3）=0且f（1）=f（﹣5）=0，由此求出a=8且b=15，由此可得f（x）=﹣x4﹣8x3﹣14x2+8x+‎ ‎15．利用导数研究f（x）的单调性，可得f（x）在区间（﹣∞，﹣2﹣）、（﹣2，﹣2+）上是增函数，在区间（﹣2﹣，﹣2）、（﹣2+，+∞）上是减函数，结合f（﹣2﹣）=f（﹣2+）=16，即可得到f（x）的最大值．‎ ‎【解答】解：∵函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣2对称，‎ ‎∴f（﹣1）=f（﹣3）=0且f（1）=f（﹣5）=0，‎ 即[1﹣（﹣3）2][（﹣3）2+a•（﹣3）+b]=0且[1﹣（﹣5）2][（﹣5）2+a•（﹣5）+b]=0，‎ 解之得，‎ 因此，f（x）=（1﹣x2）（x2+8x+15）=﹣x4﹣8x3﹣14x2+8x+15，‎ 求导数，得f′（x）=﹣4x3﹣24x2﹣28x+8，‎ 令f′（x）=0，得x1=﹣2﹣，x2=﹣2，x3=﹣2+，‎ 当x∈（﹣∞，﹣2﹣）时，f′（x）＞0；当x∈（﹣2﹣，﹣2）时，f′（x）＜0； ‎ 当x∈（﹣2，﹣2+）时，f′（x）＞0； 当x∈（﹣2+，+∞）时，f′（x）＜0‎ ‎∴f（x）在区间（﹣∞，﹣2﹣）、（﹣2，﹣2+）上是增函数，在区间（﹣2﹣，﹣2）、（﹣2+，+∞）上是减函数．‎ 又∵f（﹣2﹣）=f（﹣2+）=16，‎ ‎∴f（x）的最大值为16．‎ 故答案为：16．‎ ‎【点评】本题给出多项式函数的图象关于x=﹣2对称，求函数的最大值．着重考查了函数的奇偶性、利用导数研究函数的单调性和函数的最值求法等知识，属于中档题．‎ ‎　‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤.‎ ‎17．（12分）如图，在△ABC中，∠ABC=90°，AB=，BC=1，P为△ABC内一点，∠BPC=90°．‎ ‎（1）若PB=，求PA；‎ ‎（2）若∠APB=150°，求tan∠PBA．‎ ‎【分析】（I）在Rt△PBC，利用边角关系即可得到∠PBC=60°，得到∠PBA=30°．在△PBA中，利用余弦定理即可求得PA．‎ ‎（II）设∠PBA=α，在Rt△PBC中，可得PB=sinα．在△PBA中，由正弦定理得，即，化简即可求出．‎ ‎【解答】解：（I）在Rt△PBC中，=，∴∠PBC=60°，∴∠PBA=30°．‎ 在△PBA中，由余弦定理得PA2=PB2+AB2﹣2PB•ABcos30°==．‎ ‎∴PA=．‎ ‎（II）设∠PBA=α，在Rt△PBC中，PB=BCcos（90°﹣α）=sinα．‎ 在△PBA中，由正弦定理得，即，‎ 化为．∴．‎ ‎【点评】熟练掌握直角三角形的边角关系、正弦定理和余弦定理是解题的关键．‎ ‎　‎ ‎18．（12分）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．‎ ‎（Ⅰ）证明AB⊥A1C；‎ ‎（Ⅱ）若平面ABC⊥平面AA1B1B，AB=CB=2，求直线A1C与平面BB1C1C所成角的正弦值．‎ ‎【分析】（Ⅰ）取AB的中点O，连接OC，OA1，A1B，由已知可证OA1⊥AB，AB⊥平面OA1C，进而可得AB⊥A1C；‎ ‎（Ⅱ）易证OA，OA1，OC两两垂直．以O为坐标原点，的方向为x轴的正向，||为单位长，建立坐标系，可得，，的坐标，设=（x，y，z）为平面BB1C1C的法向量，则，可解得=（，1，﹣1），可求|cos＜，＞|，即为所求正弦值．‎ ‎【解答】解：（Ⅰ）取AB的中点O，连接OC，OA1，A1B，‎ 因为CA=CB，所以OC⊥AB，由于AB=AA1，∠BAA1=60°，‎ 所以△AA1B为等边三角形，所以OA1⊥AB，‎ 又因为OC∩OA1=O，所以AB⊥平面OA1C，‎ 又A1C⊂平面OA1C，故AB⊥A1C；‎ ‎（Ⅱ）由（Ⅰ）知OC⊥AB，OA1⊥AB，又平面ABC⊥平面AA1B1B，交线为AB，‎ 所以OC⊥平面AA1B1B，故OA，OA1，OC两两垂直．‎ 以O为坐标原点，的方向为x轴的正向，||为单位长，建立如图所示的坐标系，‎ 可得A（1，0，0），A1（0，，0），C（0，0，），B（﹣1，0，0），‎ 则=（1，0，），=（﹣1，，0），=（0，﹣，），‎ 设=（x，y，z）为平面BB1C1C的法向量，则，即，‎ 可取y=1，可得=（，1，﹣1），故cos＜，＞==，‎ 又因为直线与法向量的余弦值的绝对值等于直线与平面的正弦值，‎ 故直线A1C与平面BB1C1C所成角的正弦值为：．‎ ‎【点评】本题考查直线与平面所成的角，涉及直线与平面垂直的性质和平面与平面垂直的判定，属难题．‎ ‎　‎ ‎19．（12分）一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n．如果n=3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n=4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的产品是优质品的概率都为，且各件产品是否为优质品相互独立．‎ ‎（Ⅰ）求这批产品通过检验的概率；‎ ‎（Ⅱ）已知每件产品检验费用为100元，凡抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X（单位：元），求X的分布列及数学期望．‎ ‎【分析】（Ⅰ）设第一次取出的4件产品中恰有3件优质品为事件A1，第一次取出的4件产品全是优质品为事件A2，第二次取出的4件产品全是优质品为事件B1，第二次取出的1件产品是优质品为事件B2，这批产品通过检验为事件A，依题意有A=（A1B1）∪（A2B2），且A1B1与A2B2互斥，由概率得加法公式和条件概率，代入数据计算可得；‎ ‎（Ⅱ）X可能的取值为400，500，800，分别求其概率，可得分布列，进而可得期望值．‎ ‎【解答】解：（Ⅰ）设第一次取出的4件产品中恰有3件优质品为事件A1，第一次取出的4件产品全是优质品为事件A2，‎ 第二次取出的4件产品全是优质品为事件B1，第二次取出的1件产品是优质品为事件B2，‎ 这批产品通过检验为事件A，依题意有A=（A1B1）∪（A2B2），且A1B1与A2B2互斥，‎ 所以P（A）=P（A1B1）+P（A2B2）=P（A1）P（B1|A1）+P（A2）P（B2|A2）‎ ‎==‎ ‎（Ⅱ）X可能的取值为400，500，800，并且P（X=800）=，P（X=500）=，‎ P（X=400）=1﹣﹣=，故X的分布列如下：‎ X ‎ ‎400 ‎ ‎500 ‎ ‎800 ‎ ‎ P ‎ ‎ ‎ ‎ ‎ ‎ 故EX=400×+500×+800×=506.25‎ ‎【点评】本题考查离散型随机变量及其分布列涉及数学期望的求解，属中档题．‎ ‎　‎ ‎20．（12分）已知圆M：（x+1）2+y2=1，圆N：（x﹣1）2+y2=9，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C．‎ ‎（Ⅰ）求C的方程；‎ ‎（Ⅱ）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|．‎ ‎【分析】（I）设动圆的半径为R，由已知动圆P与圆M外切并与圆N内切，可得|PM|+|PN|=R+1+（3﹣R）=4，而|NM|=2，由椭圆的定义可知：动点P的轨迹是以M，N为焦点，4为长轴长的椭圆，求出即可；‎ ‎（II）设曲线C上任意一点P（x，y），由于|PM|﹣|PN|=2R﹣2≤4﹣2=2，所以R ‎≤2，当且仅当⊙P的圆心为（2，0）R=2时，其半径最大，其方程为（x﹣2）2+y2=4．分①l的倾斜角为90°，此时l与y轴重合，可得|AB|．②若l的倾斜角不为90°，由于⊙M的半径1≠R，可知l与x轴不平行，设l与x轴的交点为Q，根据，可得Q（﹣4，0），所以可设l：y=k（x+4），与椭圆的方程联立，得到根与系数的关系利用弦长公式即可得出．‎ ‎【解答】解：（I）由圆M：（x+1）2+y2=1，可知圆心M（﹣1，0）；圆N：（x﹣1）2+y2=9，圆心N（1，0），半径3．‎ 设动圆的半径为R，‎ ‎∵动圆P与圆M外切并与圆N内切，∴|PM|+|PN|=R+1+（3﹣R）=4，‎ 而|NM|=2，由椭圆的定义可知：动点P的轨迹是以M，N为焦点，4为长轴长的椭圆，‎ ‎∴a=2，c=1，b2=a2﹣c2=3．‎ ‎∴曲线C的方程为（x≠﹣2）．‎ ‎（II）设曲线C上任意一点P（x，y），‎ 由于|PM|﹣|PN|=2R﹣2≤3﹣1=2，所以R≤2，当且仅当⊙P的圆心为（2，0）R=2时，其半径最大，其方程为（x﹣2）2+y2=4．‎ ‎①l的倾斜角为90°，则l与y轴重合，可得|AB|=．‎ ‎②若l的倾斜角不为90°，由于⊙M的半径1≠R，可知l与x轴不平行，‎ 设l与x轴的交点为Q，则，可得Q（﹣4，0），所以可设l：y=k（x+4），‎ 由l于M相切可得：，解得．‎ 当时，联立，得到7x2+8x﹣8=0．‎ ‎∴，．‎ ‎∴|AB|===‎ 由于对称性可知：当时，也有|AB|=．‎ 综上可知：|AB|=或．‎ ‎【点评】本题综合考查了两圆的相切关系、直线与圆相切问题、椭圆的定义及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式等基础知识，需要较强的推理能力和计算能力及其分类讨论的思想方法．‎ ‎　‎ ‎21．（12分）已知函数f（x）=x2+ax+b，g（x）=ex（cx+d），若曲线y=f（x）和曲线y=g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2．‎ ‎（Ⅰ）求a，b，c，d的值；‎ ‎（Ⅱ）若x≥﹣2时，f（x）≤kg（x），求k的取值范围．‎ ‎【分析】（Ⅰ）对f（x），g（x）进行求导，已知在交点处有相同的切线及曲线y=f（x）和曲线y=g（x）都过点P（0，2），从而解出a，b，c，d的值；‎ ‎（Ⅱ）由（I）得出f（x），g（x）的解析式，再求出F（x）及它的导函数，通过对k的讨论，判断出F（x）的最值，从而判断出f（x）≤kg（x）恒成立，从而求出k的范围．‎ ‎【解答】解：（Ⅰ）由题意知f（0）=2，g（0）=2，f′（0）=4，g′（0）=4，‎ 而f′（x）=2x+a，g′（x）=ex（cx+d+c），故b=2，d=2，a=4，d+c=4，‎ 从而a=4，b=2，c=2，d=2；‎ ‎（Ⅱ）由（I）知，f（x）=x2+4x+2，g（x）=2ex（x+1）‎ 设F（x）=kg（x）﹣f（x）=2kex（x+1）﹣x2﹣4x﹣2，‎ 则F′（x）=2kex（x+2）﹣2x﹣4=2（x+2）（kex﹣1），‎ 由题设得F（0）≥0，即k≥1，‎ 令F′（x）=0，得x1=﹣lnk，x2=﹣2，‎ ‎①若1≤k＜e2，则﹣2＜x1≤0，从而当x∈（﹣2，x1）时，F′（x）＜0，当x∈‎ ‎（x1，+∞）时，F′（x）＞0，‎ 即F（x）在（﹣2，x1）上减，在（x1，+∞）上是增，故F（x）在[﹣2，+∞）上的最小值为F（x1），‎ 而F（x1）=﹣x1（x1+2）≥0，x≥﹣2时F（x）≥0，即f（x）≤kg（x）恒成立．‎ ‎②若k=e2，则F′（x）=2e2（x+2）（ex﹣e﹣2），从而当x∈（﹣2，+∞）时，F′（x）＞0，‎ 即F（x）在（﹣2，+∞）上是增，而F（﹣2）=0，故当x≥﹣2时，F（x）≥0，即f（x）≤kg（x）恒成立．‎ ‎③若k＞e2时，F′（x）＞2e2（x+2）（ex﹣e﹣2），‎ 而F（﹣2）=﹣2ke﹣2+2＜0，所以当x＞﹣2时，f（x）≤kg（x）不恒成立，‎ 综上，k的取值范围是[1，e2]．‎ ‎【点评】此题主要考查利用导数研究曲线上某点切线方程，函数恒成立问题，考查分类讨论思想，解题的关键是能够利用导数工具研究函数的性质，此题是一道中档题．‎ ‎　‎ 四、请考生在第22、23、24题中任选一道作答，并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分，不涂，按本选考题的首题进行评分.‎ ‎22．（10分）（选修4﹣1：几何证明选讲）‎ 如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D．‎ ‎（Ⅰ）证明：DB=DC；‎ ‎（Ⅱ）设圆的半径为1，BC=，延长CE交AB于点F，求△BCF外接圆的半径．‎ ‎【分析】（I）连接DE交BC于点G，由弦切角定理可得∠ABE=∠BCE，由已知角平分线可得∠ABE=∠CBE，于是得到∠CBE=∠BCE，BE=CE．由已知DB⊥BE，可知DE为⊙O的直径，Rt△DBE≌Rt△DCE，利用三角形全等的性质即可得到DC=DB．‎ ‎（II）由（I）可知：DG是BC的垂直平分线，即可得到BG=．设DE的中点为O，连接BO，可得∠BOG=60°．从而∠ABE=∠BCE=∠CBE=30°．得到CF⊥BF．进而得到Rt△BCF的外接圆的半径=．‎ ‎【解答】（I）证明：连接DE交BC于点G．‎ 由弦切角定理可得∠ABE=∠BCE，而∠ABE=∠CBE，‎ ‎∴∠CBE=∠BCE，BE=CE．‎ 又∵DB⊥BE，∴DE为⊙O的直径，∠DCE=90°．‎ ‎∴△DBE≌△DCE，∴DC=DB．‎ ‎（II）由（I）可知：∠CDE=∠BDE，DB=DC．‎ 故DG是BC的垂直平分线，∴BG=．‎ 设DE的中点为O，连接BO，则∠BOG=60°．‎ 从而∠ABE=∠BCE=∠CBE=30°．‎ ‎∴CF⊥BF．‎ ‎∴Rt△BCF的外接圆的半径=．‎ ‎【点评】‎ 本题综合考查了圆的性质、弦切角定理、等边三角形的性质、三角形全等、三角形的外接圆的半径等知识，需要较强的推理能力、分析问题和解决问题的能力．‎ ‎　‎ ‎23．已知曲线C1的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ．‎ ‎（1）把C1的参数方程化为极坐标方程；‎ ‎（2）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）．‎ ‎【分析】（1）曲线C1的参数方程消去参数t，得到普通方程，再由，能求出C1的极坐标方程．‎ ‎（2）曲线C2的极坐标方程化为直角坐标方程，与C1的普通方程联立，求出C1与C2交点的直角坐标，由此能求出C1与C2交点的极坐标．‎ ‎【解答】解：（1）将，消去参数t，化为普通方程（x﹣4）2+（y﹣5）2=25，‎ 即C1：x2+y2﹣8x﹣10y+16=0，‎ 将代入x2+y2﹣8x﹣10y+16=0，‎ 得ρ2﹣8ρcosθ﹣10ρsinθ+16=0．‎ ‎∴C1的极坐标方程为ρ2﹣8ρcosθ﹣10ρsinθ+16=0．‎ ‎（2）∵曲线C2的极坐标方程为ρ=2sinθ．‎ ‎∴曲线C2的直角坐标方程为x2+y2﹣2y=0，‎ 联立，‎ 解得或，‎ ‎∴C1与C2交点的极坐标为（）和（2，）．‎ ‎【点评】本题考查曲线极坐标方程的求法，考查两曲线交点的极坐标的求法，考查极坐标方程、直角坐标方程、参数方程的互化等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．‎ ‎　‎ ‎24．已知函数f（x）=|2x﹣1|+|2x+a|，g（x）=x+3．‎ ‎（Ⅰ）当a=﹣2时，求不等式f（x）＜g（x）的解集；‎ ‎（Ⅱ）设a＞﹣1，且当x∈[﹣，]时，f（x）≤g（x），求a的取值范围．‎ ‎【分析】（Ⅰ）当a=﹣2时，求不等式f（x）＜g（x）化为|2x﹣1|+|2x﹣2|﹣x﹣3＜0．设y=|2x﹣1|+|2x﹣2|﹣x﹣3，画出函数y的图象，数形结合可得结论．‎ ‎（Ⅱ）不等式化即 1+a≤x+3，故x≥a﹣2对x∈[﹣，]都成立，分析可得﹣≥a﹣2，由此解得a的取值范围．‎ ‎【解答】解：（Ⅰ）当a=﹣2时，求不等式f（x）＜g（x）化为|2x﹣1|+|2x﹣2|﹣x﹣3＜0．‎ 设y=|2x﹣1|+|2x﹣2|﹣x﹣3，则 y=，它的图象如图所示：‎ 结合图象可得，y＜0的解集为（0，2），故原不等式的解集为（0，2）．‎ ‎（Ⅱ）设a＞﹣1，且当x∈[﹣，]时，f（x）=1+a，不等式化为 1+a≤x+3，‎ 故 x≥a﹣2对x∈[﹣，]都成立．‎ 故﹣≥a﹣2，‎ 解得 a≤，‎ 故a的取值范围为（﹣1，]．‎ ‎【点评】本题考查绝对值不等式的解法与绝对值不等式的性质，关键是利用零点分段讨论法分析函数的解析式．‎ ‎　‎