2013年湖北省高考数学试卷（理科） 30页

‎2013年湖北省高考数学试卷（理科）‎ ‎　‎ 一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）在复平面内，复数z=（i为虚数单位）的共轭复数对应的点位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2．（5分）已知全集为R，集合A={x|（）x≤1}，B={x|x2﹣6x+8≤0}，则A∩（∁RB）=（　　）‎ A．{x|x≤0} B．{x|2≤x≤4} C．{x|0≤x＜2或x＞4} D．{x|0＜x≤2或x≥4}‎ ‎3．（5分）在一次跳伞训练中，甲、乙两位学员各跳一次，设命题p是“甲降落在指定范围”，q是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为（　　）‎ A．（￢p）∨（￢q） B．p∨（￢q） C．（￢p）∧（￢q） D．p∨q ‎4．（5分）将函数y=cosx+sinx（x∈R）的图象向左平移m（m＞0）个单位长度后，所得到的图象关于y轴对称，则m的最小值是（　　）‎ A． B． C． D．‎ ‎5．（5分）已知0＜θ＜，则双曲线与C2：﹣=1的（　　）‎ A．实轴长相等 B．虚轴长相等 C．焦距相等 D．离心率相等 ‎6．（5分）已知点A（﹣1，1），B（1，2），C（﹣2，﹣1），D（3，4），则向量在方向上的投影为（　　）‎ A． B． C． D．‎ ‎7．（5分）一辆汽车在高速公路上行驶，由于遇到紧急情况而刹车，以速度 的单位：s，v的单位：m/s）行驶至停止，在此期间汽车继续行驶的距离（单位：m）是（　　）‎ A．1+25ln5 B．8+25ln C．4+25ln5 D．4+50ln2‎ ‎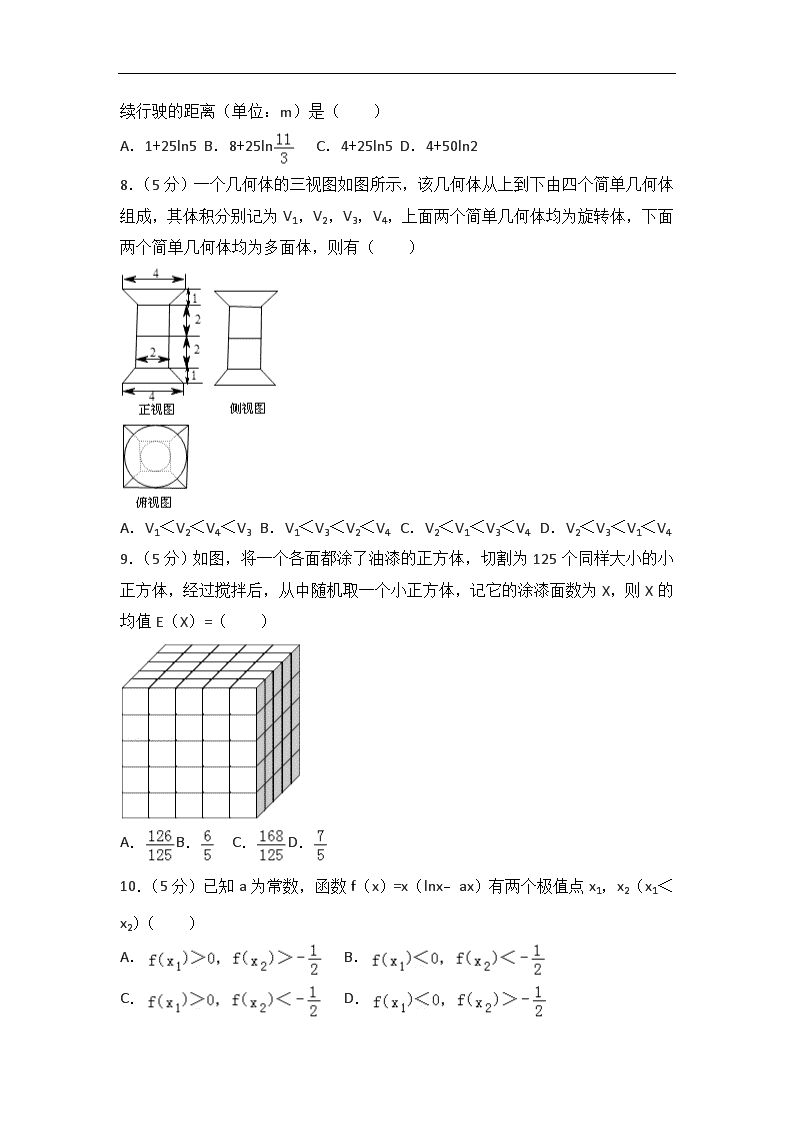8．（5分）一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为V1，V2，V3，V4，上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则有（　　）‎ A．V1＜V2＜V4＜V3 B．V1＜V3＜V2＜V4 C．V2＜V1＜V3＜V4 D．V2＜V3＜V1＜V4‎ ‎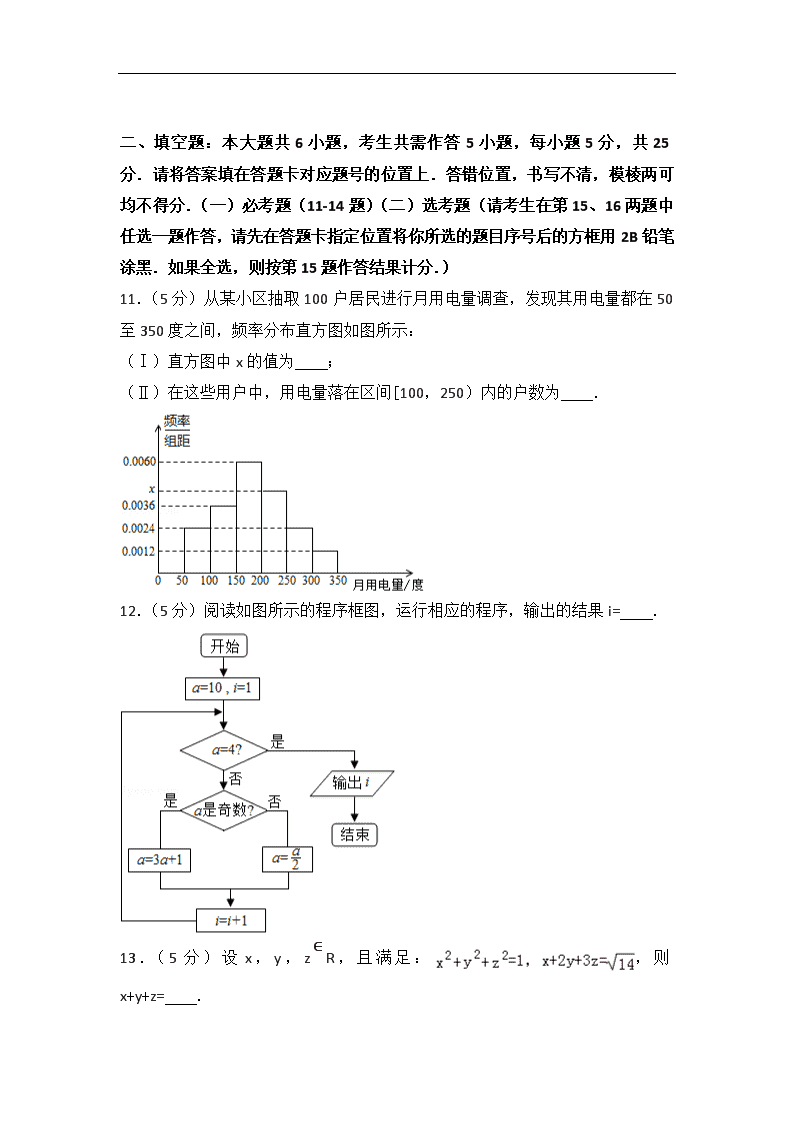9．（5分）如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的涂漆面数为X，则X的均值E（X）=（　　）‎ A． B． C． D．‎ ‎10．（5分）已知a为常数，函数f（x）=x（lnx﹣ax）有两个极值点x1，x2（x1＜x2）（　　）‎ A． B．‎ C． D．‎ ‎　‎ 二、填空题：本大题共6小题，考生共需作答5小题，每小题5分，共25分．请将答案填在答题卡对应题号的位置上．答错位置，书写不清，模棱两可均不得分．（一）必考题（11-14题）（二）选考题（请考生在第15、16两题中任选一题作答，请先在答题卡指定位置将你所选的题目序号后的方框用2B铅笔涂黑．如果全选，则按第15题作答结果计分．）‎ ‎11．（5分）从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直方图如图所示：‎ ‎（Ⅰ）直方图中x的值为　　；‎ ‎（Ⅱ）在这些用户中，用电量落在区间[100，250）内的户数为　　．‎ ‎12．（5分）阅读如图所示的程序框图，运行相应的程序，输出的结果i=　　．‎ ‎13．（5分）设x，y，z∈R，且满足：，则x+y+z=　　．‎ ‎14．（5分）古希腊毕达哥拉斯学派的数学家研究过各种多边形数，如三角形数1，3，6，10，…，第n个三角形数为．记第n个k边形数为N（n，k）（k≥3），以下列出了部分k边形数中第n个数的表达式：‎ 三角形数，‎ 正方形数N（n，4）=n2，‎ 五边形数，‎ 六边形数N（n，6）=2n2﹣n，‎ ‎…‎ 可以推测N（n，k）的表达式，由此计算N（10，24）=　　．‎ ‎15．（5分）（选修4﹣1：几何证明选讲）‎ 如图，圆O上一点C在直径AB上的射影为D，点D在半径OC上的射影为E．若AB=3AD，则的值为　　．‎ ‎16．（选修4﹣4：坐标系与参数方程）‎ 在直角坐标系xOy中，椭圆C的参数方程为为参数，a＞b＞0）．在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，直线l与圆O的极坐标方程分别为为非零常数）与ρ=b．若直线l经过椭圆C的焦点，且与圆O相切，则椭圆C的离心率为　　．‎ ‎　‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）在△‎ ABC中，角A，B，C对应的边分别是a，b，c，已知cos2A﹣3cos（B+C）=1．‎ ‎（Ⅰ）求角A的大小；‎ ‎（Ⅱ）若△ABC的面积S=5，b=5，求sinBsinC的值．‎ ‎18．（12分）已知等比数列{an}满足：|a2﹣a3|=10，a1a2a3=125．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）是否存在正整数m，使得？若存在，求m的最小值；若不存在，说明理由．‎ ‎19．（12分）如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．‎ ‎（Ⅰ）记平面BEF与平面ABC的交线为l，试判断直线l与平面PAC的位置关系，并加以证明；‎ ‎（Ⅱ）设（Ⅰ）中的直线l与圆O的另一个交点为D，且点Q满足．记直线PQ与平面ABC所成的角为θ，异面直线PQ与EF所成的角为α，二面角E﹣l﹣C的大小为β．求证：sinθ=sinαsinβ．‎ ‎20．（12分）假设每天从甲地去乙地的旅客人数X是服从正态分布N（800，502）的随机变量．记一天中从甲地去乙地的旅客人数不超过900的概率为p0．‎ ‎（Ⅰ）求p0的值；‎ ‎（参考数据：若X～N（μ，σ2），有P（μ﹣σ＜X≤μ+σ）=0.6826，P（μ﹣2σ＜X≤μ+2σ）=0.9544，P（μ﹣3σ＜X≤μ+3σ）=0.9974．）‎ ‎（Ⅱ）某客运公司用A，B两种型号的车辆承担甲、乙两地间的长途客运业务，每车每天往返一次，A，B两种车辆的载客量分别为36人和60人，从甲地去乙地的营运成本分别为1600元/辆和2400元/辆．公司拟组建一个不超过21辆车的客运车队，并要求B型车不多于A型车7辆．若每天要以不小于p0‎ 的概率运完从甲地去乙地的旅客，且使公司从甲地去乙地的营运成本最小，那么应配备A型车、B型车各多少辆？‎ ‎21．（13分）如图，已知椭圆C1与C2的中心在坐标原点O，长轴均为MN且在x轴上，短轴长分别为2m，2n（m＞n），过原点且不与x轴重合的直线l与C1，C2的四个交点按纵坐标从大到小依次为A，B，C，D，记，△BDM和△ABN的面积分别为S1和S2．‎ ‎（Ⅰ）当直线l与y轴重合时，若S1=λS2，求λ的值；‎ ‎（Ⅱ）当λ变化时，是否存在与坐标轴不重合的直线l，使得S1=λS2？并说明理由．‎ ‎22．（14分）设n是正整数，r为正有理数．‎ ‎（Ⅰ）求函数f（x）=（1+x）r+1﹣（r+1）x﹣1（x＞﹣1）的最小值；‎ ‎（Ⅱ）证明：；‎ ‎（Ⅲ）设x∈R，记[x]为不小于x的最小整数，例如．令的值．‎ ‎（参考数据：．‎ ‎　‎ ‎2013年湖北省高考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）（2013•湖北）在复平面内，复数z=（i为虚数单位）的共轭复数对应的点位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【分析】将复数z=的分母实数化，求得z=1+i，即可求得，从而可知答案．‎ ‎【解答】解：∵z====1+i，‎ ‎∴=1﹣i．‎ ‎∴对应的点（1，﹣1）位于第四象限，‎ 故选D．‎ ‎　‎ ‎2．（5分）（2013•湖北）已知全集为R，集合A={x|（）x≤1}，B={x|x2﹣6x+8≤0}，则A∩（∁RB）=（　　）‎ A．{x|x≤0} B．{x|2≤x≤4} C．{x|0≤x＜2或x＞4} D．{x|0＜x≤2或x≥4}‎ ‎【分析】利用指数函数的性质可求得集合A，通过解一元二次不等式可求得集合B，从而可求得A∩CRB．‎ ‎【解答】解：∵≤1=，‎ ‎∴x≥0，‎ ‎∴A={x|x≥0}；‎ 又x2﹣6x+8≤0⇔（x﹣2）（x﹣4）≤0，‎ ‎∴2≤x≤4．‎ ‎∴B={x|2≤x≤4}，‎ ‎∴∁RB={x|x＜2或x＞4}，‎ ‎∴A∩∁RB={x|0≤x＜2或x＞4}，‎ 故选C．‎ ‎　‎ ‎3．（5分）（2013•湖北）在一次跳伞训练中，甲、乙两位学员各跳一次，设命题p是“甲降落在指定范围”，q是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为（　　）‎ A．（￢p）∨（￢q） B．p∨（￢q） C．（￢p）∧（￢q） D．p∨q ‎【分析】由命题P和命题q写出对应的￢p和￢q，则命题“至少有一位学员没有降落在指定范围”即可得到表示．‎ ‎【解答】解：命题p是“甲降落在指定范围”，则￢p是“甲没降落在指定范围”，‎ q是“乙降落在指定范围”，则￢q是“乙没降落在指定范围”，‎ 命题“至少有一位学员没有降落在指定范围”包括 ‎“甲降落在指定范围，乙没降落在指定范围”‎ 或“甲没降落在指定范围，乙降落在指定范围”‎ 或“甲没降落在指定范围，乙没降落在指定范围”三种情况．‎ 所以命题“至少有一位学员没有降落在指定范围”可表示为（￢p）V（￢q）．‎ 故选A．‎ ‎　‎ ‎4．（5分）（2013•湖北）将函数y=cosx+sinx（x∈R）的图象向左平移m（m＞0）个单位长度后，所得到的图象关于y轴对称，则m的最小值是（　　）‎ A． B． C． D．‎ ‎【分析】函数解析式提取2变形后，利用两角和与差的正弦函数公式化为一个角的正弦函数，利用平移规律得到平移后的解析式，根据所得的图象关于y轴对称，即可求出m的最小值．‎ ‎【解答】解：y=cosx+sinx=2（cosx+sinx）=2sin（x+），‎ ‎∴图象向左平移m（m＞0）个单位长度得到y=2sin[（x+m）+]=2sin（x+m+‎ ‎），‎ ‎∵所得的图象关于y轴对称，‎ ‎∴m+=kπ+（k∈Z），‎ 则m的最小值为．‎ 故选B ‎　‎ ‎5．（5分）（2013•湖北）已知0＜θ＜，则双曲线与C2：﹣=1的（　　）‎ A．实轴长相等 B．虚轴长相等 C．焦距相等 D．离心率相等 ‎【分析】根据双曲线的标准方程求出双曲线的几何性质同，即可得出正确答案．‎ ‎【解答】解：双曲线的实轴长为2cosθ，虚轴长2sinθ，焦距2，离心率，‎ 双曲线的实轴长为2sinθ，虚轴长2sinθtanθ，焦距2tanθ，离心率，‎ 故它们的离心率相同．‎ 故选D．‎ ‎　‎ ‎6．（5分）（2013•湖北）已知点A（﹣1，1），B（1，2），C（﹣2，﹣1），D（3，4），则向量在方向上的投影为（　　）‎ A． B． C． D．‎ ‎【分析】先求出向量、，根据投影定义即可求得答案．‎ ‎【解答】解：，，‎ 则向量方向上的投影为：•cos＜＞=•===，‎ 故选A．‎ ‎　‎ ‎7．（5分）（2013•湖北）一辆汽车在高速公路上行驶，由于遇到紧急情况而刹车，以速度的单位：s，v的单位：m/s）行驶至停止，在此期间汽车继续行驶的距离（单位：m）是（　　）‎ A．1+25ln5 B．8+25ln C．4+25ln5 D．4+50ln2‎ ‎【分析】令v（t）=0，解得t=4，则所求的距离S=，解出即可．‎ ‎【解答】解：令v（t）=7﹣3t+，化为3t2﹣4t﹣32=0，又t＞0，解得t=4．‎ ‎∴由刹车行驶至停止，在此期间汽车继续行驶的距离s===4+25ln5．‎ 故选C．‎ ‎　‎ ‎8．（5分）（2013•湖北）一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为V1，V2，V3，V4，上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则有（　　）‎ A．V1＜V2＜V4＜V3 B．V1＜V3＜V2＜V4 C．V2＜V1＜V3＜V4 D．V2＜V3＜V1＜V4‎ ‎【分析】利用三视图与已知条件判断组合体的形状，分别求出几何体的体积，即可判断出正确选项．‎ ‎【解答】解：由题意以及三视图可知，该几何体从上到下由：圆台、圆柱、正四棱柱、正四棱台组成，‎ 体积分别记为V1==．‎ V2=12×π×2=2π，‎ V3=2×2×2=8‎ V4==；‎ ‎∵，‎ ‎∴V2＜V1＜V3＜V4‎ 故选C．‎ ‎　‎ ‎9．（5分）（2013•湖北）如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的涂漆面数为X，则X的均值E（X）=（　　）‎ A． B． C． D．‎ ‎【分析】由题意可知：X所有可能取值为0，1，2，3．①8个顶点处的8个小正方体涂有3面，②每一条棱上除了两个顶点处的小正方体，还剩下3个，一共有3×12=36个小正方体涂有2面，‎ ‎③每个表面去掉四条棱上的16个小正方形，还剩下9个小正方形，因此一共有9×6=54个小正方体涂有一面，④由以上可知：还剩下125﹣（8+36+54）=27个内部的小正方体的6个面都没有涂油漆，根据上面的分析即可得出其概率及X的分布列，利用数学期望的计算公式即可得出．‎ ‎【解答】解：由题意可知：X所有可能取值为0，1，2，3．‎ ‎①8个顶点处的8个小正方体涂有3面，∴P（X=3）=；‎ ‎②每一条棱上除了两个顶点处的小正方体，还剩下3个，一共有3×12=36个小正方体涂有2面，∴P（X=2）=；‎ ‎③每个表面去掉四条棱上的16个小正方形，还剩下9个小正方形，因此一共有9×6=54个小正方体涂有一面，∴P（X=1）=．‎ ‎④由以上可知：还剩下125﹣（8+36+54）=27个内部的小正方体的6个面都没有涂油漆，∴P（X=0）=． ‎ X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 故X的分布列为 因此E（X）==．‎ 故选B．‎ ‎　‎ ‎10．（5分）（2013•湖北）已知a为常数，函数f（x）=x（lnx﹣ax）有两个极值点x1，x2（x1＜x2）（　　）‎ A． B．‎ C． D．‎ ‎【分析】先求出f′（x），令f′（x）=0，由题意可得lnx=2ax﹣1有两个解x1，x2⇔函数g（x）=lnx+1﹣2ax有且只有两个零点⇔g′（x）在（0，+∞）上的唯一的极值不等于0．利用导数与函数极值的关系即可得出．‎ ‎【解答】解：∵f′（x）=lnx+1﹣2ax，（x＞0）‎ 令f′（x）=0，由题意可得lnx=2ax﹣1有两个解x1，x2⇔函数g（x）=lnx+1﹣2ax有且只有两个零点⇔g′（x）在（0，+∞）上的唯一的极值不等于0．‎ ‎．‎ ‎①当a≤0时，g′（x）＞0，f′（x）单调递增，因此g（x）=f′（x）至多有一个零点，不符合题意，应舍去．‎ ‎②当a＞0时，令g′（x）=0，解得x=，‎ ‎∵x，g′（x）＞0，函数g（x）单调递增；时，g′（x）＜0，函数g（x）单调递减．‎ ‎∴x=是函数g（x）的极大值点，则＞0，即＞0，‎ ‎∴ln（2a）＜0，∴0＜2a＜1，即．‎ 故当0＜a＜时，g（x）=0有两个根x1，x2，且x1＜＜x2，又g（1）=1﹣2a＞0，‎ ‎∴x1＜1＜＜x2，从而可知函数f（x）在区间（0，x1）上递减，在区间（x1，x2）上递增，在区间（x2，+∞）上递减． ‎ ‎∴f（x1）＜f（1）=﹣a＜0，f（x2）＞f（1）=﹣a＞﹣．‎ 故选：D．‎ ‎　‎ 二、填空题：本大题共6小题，考生共需作答5小题，每小题5分，共25分．请将答案填在答题卡对应题号的位置上．答错位置，书写不清，模棱两可均不得分．（一）必考题（11-14题）（二）选考题（请考生在第15、16两题中任选一题作答，请先在答题卡指定位置将你所选的题目序号后的方框用2B铅笔涂黑．如果全选，则按第15题作答结果计分．）‎ ‎11．（5分）（2013•湖北）从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直方图如图所示：‎ ‎（Ⅰ）直方图中x的值为　0.0044　；‎ ‎（Ⅱ）在这些用户中，用电量落在区间[100，250）内的户数为　70　．‎ ‎【分析】（I）根据频率分布直方图中，各组的频率之和为1，我们易得到一个关于x的方程，解方程即可得到答案．‎ ‎（II）由已知中的频率分布直方图，利用[100，250）之间各小组的纵坐标（矩形的高）乘以组距得到[100，250）的频率，利用频率乘以样本容量即可求出频数．‎ ‎【解答】解：（Ⅰ）依题意及频率分布直方图知，0.0024×50+0.0036×50+0.0060×50+x×50+0.0024×50+0.0012×50=1，‎ 解得x=0.0044．‎ ‎（II）样本数据落在[100，150）内的频率为0.0036×50=0.18，‎ 样本数据落在[150，200）内的频率为0.006×50=0.3．‎ 样本数据落在[200，250）内的频率为0.0044×50=0.22，‎ 故在这些用户中，用电量落在区间[100，250）内的户数为（0.18+0.30+0.22）×100=70．‎ 故答案为：0.0044；70．‎ ‎　‎ ‎12．（5分）（2013•湖北）阅读如图所示的程序框图，运行相应的程序，输出的结果i=　5　．‎ ‎【分析】框图首先给变量a和变量i赋值，然后对a是否等于4进行判断，不等于4，继续判断a是否为奇数，是执行路径a=3a+1，否执行路径，再执行i=i+1，依次循环执行，当a等于4时跳出循环，输出i的值．‎ ‎【解答】解：框图首先给变量a和变量i赋值，a=4，i=1．‎ 判断10=4不成立，判断10是奇数不成立，执行，i=1+1=2；‎ 判断5=4不成立，判断5是奇数成立，执行a=3×5+1=16，i=2+1=3；‎ 判断16=4不成立，判断16是奇数不成立，执行，i=3+1=4；‎ 判断8=4不成立，判断8是奇数不成立，执行，i=4+1=5；‎ 判断4=4成立，跳出循环，输出i的值为5．‎ 故答案是5．‎ ‎　‎ ‎13．（5分）（2013•湖北）设x，y，z∈R，且满足：，则x+y+z=　　．‎ ‎【分析】根据柯西不等式，算出（x+2y+3z）2≤14（x2+y2+z2）=14，从而得到x+2y+3z恰好取到最大值，由不等式的等号成立的条件解出x=、y=且z=，由此即可得到x+y+z的值．‎ ‎【解答】解：根据柯西不等式，得 ‎（x+2y+3z）2≤（12+22+32）（x2+y2+z2）=14（x2+y2+z2）‎ 当且仅当时，上式的等号成立 ‎∵x2+y2+z2=1，∴（x+2y+3z）2≤14，‎ 结合，可得x+2y+3z恰好取到最大值 ‎∴=，可得x=，y=，z=‎ 因此，x+y+z=++=‎ 故答案为：‎ ‎　‎ ‎14．（5分）（2013•湖北）古希腊毕达哥拉斯学派的数学家研究过各种多边形数，如三角形数1，3，6，10，…，第n个三角形数为．记第n个k边形数为N（n，k）（k≥3），以下列出了部分k边形数中第n个数的表达式：‎ 三角形数，‎ 正方形数N（n，4）=n2，‎ 五边形数，‎ 六边形数N（n，6）=2n2﹣n，‎ ‎…‎ 可以推测N（n，k）的表达式，由此计算N（10，24）=　1000　．‎ ‎【分析】观察已知式子的规律，并改写形式，归纳可得，把n=10，k=24代入可得答案．‎ ‎【解答】解：原已知式子可化为：，‎ ‎，，‎ ‎，‎ 由归纳推理可得，‎ 故=1100﹣100=1000‎ 故答案为：1000‎ ‎　‎ ‎15．（5分）（2013•湖北）（选修4﹣1：几何证明选讲）‎ 如图，圆O上一点C在直径AB上的射影为D，点D在半径OC上的射影为E．若AB=3AD，则的值为　8　．‎ ‎【分析】设圆O的半径为3x，根据射影定理，可以求出OD2=OE•OC=x2，CD2=CE•OC=8x2，进而得到的值．‎ ‎【解答】解：设圆O的半径OA=OB=OC=3x，‎ ‎∵AB=3AD，‎ ‎∴AD=2x，BD=4x，OD=x 又∵点C在直径AB上的射影为D，‎ 在△ABC中，由射影定理得：CD2=AD•BD=8x2，‎ 在△ODC中，由射影定理得：OD2=OE•OC=x2，CD2=CE•OC=8x2，‎ 故==8‎ 故答案为：8‎ ‎　‎ ‎16．（2013•湖北）（选修4﹣4：坐标系与参数方程）‎ 在直角坐标系xOy中，椭圆C的参数方程为为参数，a＞b＞0）．在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，直线l与圆O的极坐标方程分别为为非零常数）与ρ=b．若直线l经过椭圆C的焦点，且与圆O相切，则椭圆C的离心率为　　．‎ ‎【分析】先根据极坐标与直角坐标的转换关系将直线l的极坐标方程分别为为非零常数）化成直角坐标方程，再利用直线l经过椭圆C的焦点，且与圆O相切，从而得到c=b，又b2=a2﹣c2，消去b后得到关于a，c的等式，即可求出椭圆C的离心率．‎ ‎【解答】解：直线l的极坐标方程分别为为非零常数）化成直角坐标方程为x+y﹣m=0，‎ 它与x轴的交点坐标为（m，0），由题意知，（m，0）为椭圆的焦点，故|m|=c，‎ 又直线l与圆O：ρ=b相切，∴，‎ 从而c=b，又b2=a2﹣c2，‎ ‎∴c2=2（a2﹣c2），‎ ‎∴3c2=2a2，∴=．‎ 则椭圆C的离心率为 ．‎ 故答案为：．‎ ‎　‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）（2013•湖北）在△ABC中，角A，B，C对应的边分别是a，b，c，已知cos2A﹣3cos（B+C）=1．‎ ‎（Ⅰ）求角A的大小；‎ ‎（Ⅱ）若△ABC的面积S=5，b=5，求sinBsinC的值．‎ ‎【分析】（I）利用倍角公式和诱导公式即可得出；‎ ‎（II）由三角形的面积公式即可得到bc=20．又b=5，解得c=4．由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21，即可得出a．又由正弦定理得即可得到即可得出．‎ ‎【解答】解：（Ⅰ）由cos2A﹣3cos（B+C）=1，得2cos2A+3cosA﹣2=0，‎ 即（2cosA﹣1）（cosA+2）=0，解得（舍去）．‎ 因为0＜A＜π，所以．‎ ‎（Ⅱ）由S===，得到bc=20．又b=5，解得c=4．‎ 由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21，故．‎ 又由正弦定理得．‎ ‎　‎ ‎18．（12分）（2013•湖北）已知等比数列{an}满足：|a2﹣a3|=10，a1a2a3=125．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）是否存在正整数m，使得？若存在，求m的最小值；若不存在，说明理由．‎ ‎【分析】（I）设等比数列{an}的公比为q，结合等比数列的通项公式表示已知条件，解方程可求a1，q，进而可求通项公式 ‎（Ⅱ）结合（I）可知是等比数列，结合等比数列的求和公式可求，即可判断 ‎【解答】解：（Ⅰ）设等比数列{an}的公比为q，则由已知可得 解得 故．‎ ‎（Ⅱ）若，则，‎ 故是首项为，公比为的等比数列，‎ 从而．‎ 若，则是首项为，公比为﹣1的等比数列，‎ 从而故．‎ 综上，对任何正整数m，总有．‎ 故不存在正整数m，使得成立．‎ ‎　‎ ‎19．（12分）（2013•湖北）如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．‎ ‎（Ⅰ）记平面BEF与平面ABC的交线为l，试判断直线l与平面PAC的位置关系，并加以证明；‎ ‎（Ⅱ）设（Ⅰ）中的直线l与圆O的另一个交点为D，且点Q满足．记直线PQ与平面ABC所成的角为θ，异面直线PQ与EF所成的角为α，二面角E﹣l﹣C的大小为β．求证：sinθ=sinαsinβ．‎ ‎【分析】（I）直线l∥平面PAC．连接EF，利用三角形的中位线定理可得，EF∥AC；利用线面平行的判定定理即可得到EF∥平面ABC．由线面平行的性质定理可得EF∥l．再利用线面平行的判定定理即可证明直线l∥平面PAC．‎ ‎（II）综合法：利用线面垂直的判定定理可证明l⊥平面PBC．连接BE，BF，因为BF⊂平面PBC，所以l⊥BC．故∠CBF就是二面角E﹣l﹣C的平面角，即∠CBF=β．‎ 已知PC⊥平面ABC，可知CD是FD在平面ABC内的射影，故∠CDF就是直线PQ与平面ABC所成的角，即∠CDF=θ．由BD⊥平面PBC，有BD⊥BF，知∠BDF=α，分别利用三个直角三角形的边角关系即可证明结论；‎ 向量法：以点C为原点，向量所在直线分别为x，y，z轴，建立如图所示的空间直角坐标系，利用两个平面的法向量的夹角即可得出二面角．‎ ‎【解答】解：（Ⅰ）直线l∥平面PAC，证明如下：‎ 连接EF，因为E，F分别是PA，PC的中点，所以EF∥AC，‎ 又EF⊄平面ABC，且AC⊂平面ABC，所以EF∥平面ABC．‎ 而EF⊂平面BEF，且平面BEF∩平面ABC=l，所以EF∥l．‎ 因为l⊄平面PAC，EF⊂平面PAC，所以直线l∥平面PAC．‎ ‎（Ⅱ）（综合法）如图1，连接BD，由（Ⅰ）可知交线l即为直线BD，且l∥AC．‎ 因为AB是⊙O的直径，所以AC⊥BC，于是l⊥BC．‎ 已知PC⊥平面ABC，而l⊂平面ABC，所以PC⊥l．‎ 而PC∩BC=C，所以l⊥平面PBC．‎ 连接BE，BF，因为BF⊂平面PBC，所以l⊥BF．‎ 故∠CBF就是二面角E﹣l﹣C的平面角，即∠CBF=β．‎ 由，作DQ∥CP，且．‎ 连接PQ，DF，因为F是CP的中点，CP=2PF，所以DQ=PF，‎ 从而四边形DQPF是平行四边形，PQ∥FD．‎ 连接CD，因为PC⊥平面ABC，所以CD是FD在平面ABC内的射影，‎ 故∠CDF就是直线PQ与平面ABC所成的角，即∠CDF=θ．‎ 又BD⊥平面PBC，有BD⊥BF，知∠BDF=α，‎ 于是在Rt△DCF，Rt△FBD，Rt△BCF中，分别可得，‎ 从而．‎ ‎（Ⅱ）（向量法）如图2，由，作DQ∥CP，且．‎ 连接PQ，EF，BE，BF，BD，由（Ⅰ）可知交线l即为直线BD．‎ 以点C为原点，向量所在直线分别为x，y，z轴，建立如图所示的空间直角坐标系，设CA=a，CB=b，CP=2c，则有．‎ 于是，‎ ‎∴=，从而，‎ 又取平面ABC的一个法向量为，可得，‎ 设平面BEF的一个法向量为，‎ 所以由可得取=（0，c，b），‎ 于是，从而．‎ 故，即sinθ=sinαsinβ．‎ ‎　‎ ‎20．（12分）（2013•湖北）假设每天从甲地去乙地的旅客人数X是服从正态分布N（800，502）的随机变量．记一天中从甲地去乙地的旅客人数不超过900的概率为p0．‎ ‎（Ⅰ）求p0的值；‎ ‎（参考数据：若X～N（μ，σ2），有P（μ﹣σ＜X≤μ+σ）=0.6826，P（μ﹣2σ＜X≤μ+2σ）=0.9544，P（μ﹣3σ＜X≤μ+3σ）=0.9974．）‎ ‎（Ⅱ）某客运公司用A，B两种型号的车辆承担甲、乙两地间的长途客运业务，每车每天往返一次，A，B两种车辆的载客量分别为36人和60人，从甲地去乙地的营运成本分别为1600元/辆和2400元/辆．公司拟组建一个不超过21辆车的客运车队，并要求B型车不多于A型车7辆．若每天要以不小于p0的概率运完从甲地去乙地的旅客，且使公司从甲地去乙地的营运成本最小，那么应配备A型车、B型车各多少辆？‎ ‎【分析】（I）变量服从正态分布N（800，502），即服从均值为800，标准差为50的正态分布，适合700＜X≤900范围内取值即在（μ﹣2σ，μ+2σ）内取值，其概率为：95.44%，从而由正态分布的对称性得出不超过900的概率为p0．‎ ‎（II）设每天应派出A型x辆、B型车y辆，根据条件列出不等式组，即得线性约束条件，列出目标函数，画出可行域求解．‎ ‎【解答】解：（Ⅰ）由于随机变量X服从正态分布N（800，502），故有μ=800，σ=50，P（700＜X≤900）=0.9544．‎ 由正态分布的对称性，可得p0=（P（X≤900）=P（X≤800）+P（800＜X≤900）=‎ ‎（Ⅱ）设A型、B型车辆的数量分别为x，y辆，则相应的营运成本为1600x+2400y．‎ 依题意，x，y还需满足：x+y≤21，y≤x+7，P（X≤36x+60y）≥p0．‎ 由（Ⅰ）知，p0=P（X≤900），故P（X≤36x+60y）≥p0等价于36x+60y≥900．‎ 于是问题等价于求满足约束条件 且使目标函数z=1600x+2400y达到最小值的x，y．‎ 作可行域如图所示，可行域的三个顶点坐标分别为P（5，12），Q（7，14），R（15，6）．‎ 由图可知，当直线z=1600x+2400y经过可行域的点P时，直线z=1600x+2400y在y轴上截距最小，即z取得最小值．‎ 故应配备A型车5辆，B型车12辆．‎ ‎　‎ ‎21．（13分）（2013•湖北）如图，已知椭圆C1与C2的中心在坐标原点O，长轴均为MN且在x轴上，短轴长分别为2m，2n（m＞n），过原点且不与x轴重合的直线l与C1，C2的四个交点按纵坐标从大到小依次为A，B，C，D，记，△BDM和△ABN的面积分别为S1和S2．‎ ‎（Ⅰ）当直线l与y轴重合时，若S1=λS2，求λ的值；‎ ‎（Ⅱ）当λ变化时，是否存在与坐标轴不重合的直线l，使得S1=λS2？并说明理由．‎ ‎【分析】（Ⅰ）设出两个椭圆的方程，当直线l与y轴重合时，求出△BDM和△ABN的面积S1和S2，直接由面积比=λ列式求λ的值；‎ ‎（Ⅱ）假设存在与坐标轴不重合的直线l，使得S1=λS2，设出直线方程，由点到直线的距离公式求出M和N到直线l的距离，利用数学转化思想把两个三角形的面积比转化为线段长度比，由弦长公式得到线段长度比的另一表达式，两式相等得到，换元后利用非零的k值存在讨论λ的取值范围．‎ ‎【解答】解：以题意可设椭圆C1和C2的方程分别为 ‎，．其中a＞m＞n＞0，‎ ‎＞1．‎ ‎（Ⅰ）如图1，若直线l与y轴重合，即直线l的方程为x=0，则 ‎，‎ ‎，‎ 所以．‎ 在C1和C2的方程中分别令x=0，可得yA=m，yB=n，yD=﹣m，‎ 于是．‎ 若，则，化简得λ2﹣2λ﹣1=0，由λ＞1，解得．‎ 故当直线l与y轴重合时，若S1=λS2，则．‎ ‎（Ⅱ）如图2，若存在与坐标轴不重合的直线l，使得S1=λS2，根据对称性，‎ 不妨设直线l：y=kx（k＞0），‎ 点M（﹣a，0），N（a，0）到直线l的距离分别为d1，d2，则 ‎，所以d1=d2．‎ 又，所以，即|BD|=λ|AB|．‎ 由对称性可知|AB|=|CD|，所以|BC|=|BD|﹣|AB|=（λ﹣1）|AB|，‎ ‎|AD|=|BD|+|AB|=（λ+1）|AB|，于是．‎ 将l的方程分别与C1和C2的方程联立，可求得 根据对称性可知xC=﹣xB，xD=﹣xA，于是 ‎②‎ 从而由①和②可得 ‎③‎ 令，则由m＞n，可得t≠1，于是由③可得．‎ 因为k≠0，所以k2＞0．于是③关于k有解，当且仅当，‎ 等价于，由λ＞1，解得，‎ 即，由λ＞1，解得，所以 当时，不存在与坐标轴不重合的直线l，使得S1=λS2；‎ 当时，存在与坐标轴不重合的直线l，使得S1=λS2．‎ ‎　‎ ‎22．（14分）（2013•湖北）设n是正整数，r为正有理数．‎ ‎（Ⅰ）求函数f（x）=（1+x）r+1﹣（r+1）x﹣1（x＞﹣1）的最小值；‎ ‎（Ⅱ）证明：；‎ ‎（Ⅲ）设x∈R，记[x]为不小于x的最小整数，例如．令的值．‎ ‎（参考数据：．‎ ‎【分析】（Ⅰ）先求出函数f（x）的导函数f′（x），令f'（x）=0，解得x=0，再求出函数的单调区间，进而求出最小值为f（0）=0；‎ ‎（Ⅱ）根据（Ⅰ）知，即（1+x）r+1≥1+（r+1）x，令代入并化简得，再令得，，即结论得到证明；‎ ‎（Ⅲ）根据（Ⅱ）的结论，令，n分别取值81，82，83，…，125，分别列出不等式，再将各式相加得，，再由参考数据和条件进行求解．‎ ‎【解答】解；（Ⅰ）由题意得f'（x）=（r+1）（1+x）r﹣（r+1）=（r+1）[（1+x）r﹣1]，‎ 令f'（x）=0，解得x=0．‎ 当﹣1＜x＜0时，f'（x）＜0，∴f（x）在（﹣1，0）内是减函数；‎ 当x＞0时，f'（x）＞0，∴f（x）在（0，+∞）内是增函数．‎ 故函数f（x）在x=0处，取得最小值为f（0）=0．‎ ‎（Ⅱ）由（Ⅰ），当x∈（﹣1，+∞）时，有f（x）≥f（0）=0，‎ 即（1+x）r+1≥1+（r+1）x，且等号当且仅当x=0时成立，‎ 故当x＞﹣1且x≠0，有（1+x）r+1＞1+（r+1）x，①‎ 在①中，令（这时x＞﹣1且x≠0），得．‎ 上式两边同乘nr+1，得（n+1）r+1＞nr+1+nr（r+1），‎ 即，②‎ 当n＞1时，在①中令（这时x＞﹣1且x≠0），‎ 类似可得，③‎ 且当n=1时，③也成立．‎ 综合②，③得，④‎ ‎（Ⅲ）在④中，令，n分别取值81，82，83，…，125，‎ 得，，，…，‎ 将以上各式相加，并整理得．‎ 代入数据计算，可得 由[S]的定义，得[S]=211．‎ ‎　‎ 参与本试卷答题和审题的老师有：wfy814；sxs123；sllwyn；minqi5；wyz123；沂蒙松；qiss；ywg2058；lincy；豫汝王世崇；庞会丽；gongjy（排名不分先后）‎ ‎2017年2月3日