高考数学专题复习练习：8-2 专项基础训练 8页

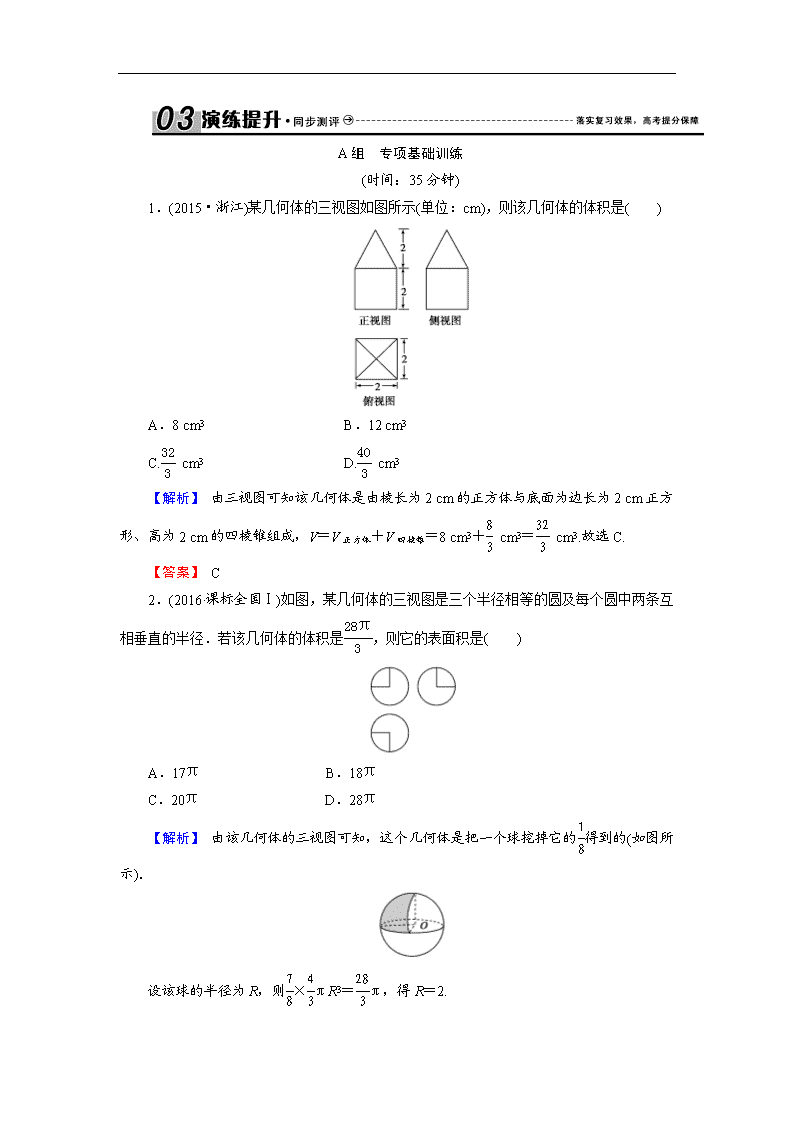
‎ A组　专项基础训练 ‎(时间：35分钟)‎ ‎1．(2015·浙江)某几何体的三视图如图所示(单位：cm)，则该几何体的体积是(　　)‎ A．8 cm3　　　　　　　　　　B．12 cm3‎ C. cm3 D. cm3‎ ‎【解析】 由三视图可知该几何体是由棱长为2 cm的正方体与底面为边长为2 cm正方形、高为2 cm的四棱锥组成，V＝V正方体＋V四棱锥＝8 cm3＋ cm3＝ cm3.故选C.‎ ‎【答案】 C ‎2．(2016·课标全国Ⅰ)如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是，则它的表面积是(　　)‎ A．17π B．18π C．20π D．28π ‎【解析】 由该几何体的三视图可知，这个几何体是把一个球挖掉它的得到的(如图所示)．‎ 设该球的半径为R，则×πR3＝π，得R＝2.‎ 所以它的表面积为4π×22－×4π×22＋3××π×22＝17π.故选A.‎ ‎【答案】 A ‎3．(2015·课标全国Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有(　　)‎ A．14斛 B．22斛 C．36斛 D．66斛 ‎【解析】 由题意知：米堆的底面半径为(尺)，体积V＝×πR2·h≈(立方尺)．所以堆放的米大约为≈22(斛)．‎ ‎【答案】 B ‎4．(2016·黑龙江哈六中期末)在平行四边形ABCD中，·＝0，22＋2－4＝0，若将其沿AC折成直二面角DACB，则三棱锥DACB的外接球的表面积为(　　)‎ A．16π B．8π C．4π D．2π ‎【解析】 由题意知，AC⊥CB，2BC2＋AC2－4＝BC2＋BC2＋AC2－4＝BC2＋AB2－4＝0.因为ABCD是平行四边形，所以BC＝AD.因为二面角DACB是直二面角，所以AD⊥平面ABC，即AD⊥AB，那么BC2＋AB2＝AD2＋AB2＝BD2＝4，即BD＝2.取BD中点O，连接OA，OC，∠BAD，∠BCD都是直角三角形，根据直角三角形斜边的中线等于斜边的一半，有OA＝OB＝OC＝OD，所以三棱锥DACB的外接球的球心为点O，半径R＝OB＝1，所以表面积为S＝4πR2＝4π.‎ ‎【答案】 C ‎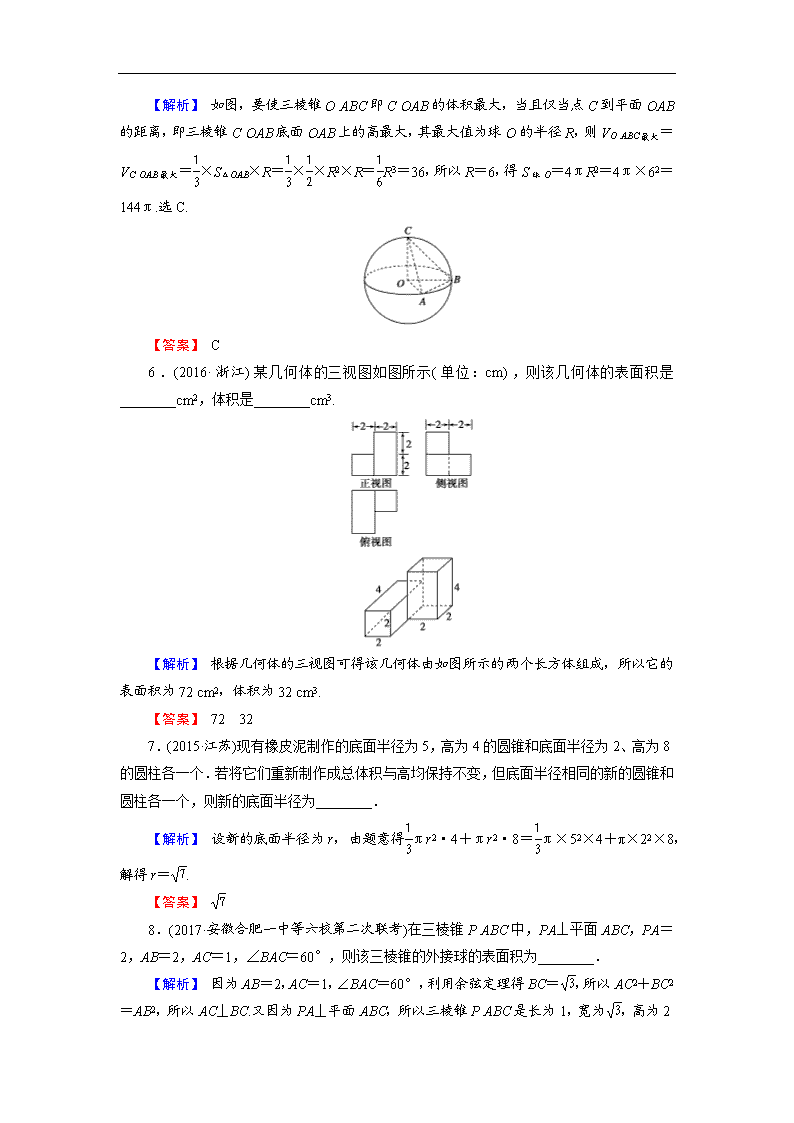5．(2015·课标全国Ⅱ)已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点．若三棱锥OABC体积的最大值为36，则球O的表面积为(　　)‎ A．36π B．64π C．144π D．256π ‎【解析】 如图，要使三棱锥OABC即COAB的体积最大，当且仅当点C到平面OAB 的距离，即三棱锥COAB底面OAB上的高最大，其最大值为球O的半径R，则VOABC最大＝VCOAB最大＝×S△OAB×R＝××R2×R＝R3＝36，所以R＝6，得S球O＝4πR2＝4π×62＝144π.选C.‎ ‎【答案】 C ‎6．(2016·浙江)某几何体的三视图如图所示(单位：cm)，则该几何体的表面积是________cm2，体积是________cm3.‎ ‎【解析】 根据几何体的三视图可得该几何体由如图所示的两个长方体组成，所以它的表面积为72 cm2，体积为32 cm3.‎ ‎【答案】 72　32‎ ‎7．(2015·江苏)现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为________．‎ ‎【解析】 设新的底面半径为r，由题意得πr2·4＋πr2·8＝π×52×4＋π×22×8，解得r＝.‎ ‎【答案】 ‎8．(2017·安徽合肥一中等六校第二次联考)在三棱锥PABC中，PA⊥平面ABC，PA＝2，AB＝2，AC＝1，∠BAC＝60°，则该三棱锥的外接球的表面积为________．‎ ‎【解析】 因为AB＝2，AC＝1，∠BAC＝60°，利用余弦定理得BC＝，所以AC2＋BC2＝AB2，所以AC⊥BC.又因为PA⊥平面ABC，所以三棱锥PABC是长为1，宽为，高为2‎ 的长方体的一部分(如图所示)，所以三棱锥PABC外接球的半径为×＝，所以其外接球的表面积为4π×()2＝8π.‎ ‎【答案】 8π ‎9．如图所示的三个几何体，一个是长方体，一个是直三棱柱，一个是过圆柱上、下底面圆心切下圆柱的四分之一部分，若这三个几何体的正视图和俯视图是相同的正方形，求它们的表面积之比．‎ ‎【解析】 由题意可知这三个几何体的高都相等，设长方体的底面正方形的边长为a，高也等于a，故其表面积为S1＝6a2.直三棱柱的底面是腰长为a的等腰直角三角形，高为a，故其表面积为S2＝×a×a＋×a×a＋(a＋a＋a)×a＝(3＋)a2.圆柱的底面是半径为a的圆的，高为a，故其表面积为S3＝πa2＋πa2＋a2＋a2＋×2πa×a＝(π＋2)a2.所以它们的表面积之比为S1∶S2∶S3＝6a2∶(3＋)a2∶(π＋2)a2＝6∶(3＋)∶(π＋2)．‎ ‎10．(教材改编)已知一个上、下底面为正三角形且两底面中心连线垂直于底面的三棱台的两底面边长分别为20 cm和30 cm，且其侧面积等于两底面面积之和，求棱台的高．‎ ‎【解析】 如图所示，三棱台ABCA1B1C1中，O、O1分别为两底面中心，D、D1分别为BC和B1C1的中点，则DD1为棱台的斜高．‎ 由题意知A1B1＝20，AB＝30，‎ 则OD＝5，O1D1＝，‎ 由S侧＝S上＋S下，得 ‎3××(20＋30)×DD1＝×(202＋302)，‎ 解得DD1＝，在直角梯形O1ODD1中，‎ O1O＝＝4，‎ 所以棱台的高为4 cm.‎ B组　专项能力提升 ‎(时间：30分钟)‎ ‎11．(2017·湖北武汉华中师大一附等校第一次联考)已知某几何体的三视图的侧视图是一个正三角形，如图所示，则该几何体的体积等于(　　)‎ A．12 B．16 C．20 D．32 ‎【解析】 题中三视图是下图中几何体ABCDEF的三视图，由三视图中的尺寸，知其体积为V＝×4×2×6－××2＝20.故选C.‎ ‎【答案】 C ‎12．(2017·河南郑州一模)如图是一个四面体的三视图，这个三视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则该四面体的体积为(　　)‎ A. B. C. D．2‎ ‎【解析】 由四面体的三视图得该四面体为棱长为2的正方体ABCDA1B1C1D1‎ 中的三棱锥C1BDE，其中E是CD的中点，△BDE的面积S＝×＝1，三棱锥C1BDE的高h＝CC1＝2，所以该四面体的体积V＝Sh＝.故选A.‎ ‎【答案】 A ‎13．(2015·四川)在三棱柱ABCA1B1C1中，∠BAC＝90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边的长为1的等腰直角三角形，设点M，N，P分别是AB，BC，B1C1的中点，则三棱锥PA1MN的体积是________．‎ ‎【解析】 由题意知还原后的几何体是一个直放的三棱柱，三棱柱的底面是直角边长为1的等腰直角三角形，高为1的直三棱柱，‎ ‎∵VPA1MN＝VA1PMN，‎ 又∵AA1∥平面PMN，‎ ‎∴VA1PMN＝VAPMN，‎ ‎∴VAPMN＝××1××＝，‎ 故VPA1MN＝.‎ ‎【答案】 ‎14．(2016·浙江)如图，在△ABC中，AB＝BC＝2，∠ABC＝120°.若平面ABC外的点P和线段AC上的点D，满足PD＝DA，PB＝BA，则四面体PBCD的体积的最大值是________．‎ ‎【解析】 本题可转化为：在△ABC中，AB＝BC＝2，∠ABC＝120°，D是边AC上的动点，连接BD，将△ABD沿BD折起构成三棱锥PBCD，求三棱锥PBCD 体积的最大值．要使棱锥的体积最大，则平面PBD⊥平面BCD，即折成直二面角．在△ABC中，∵AB＝BC＝2，∠ABC＝120°，‎ ‎∴∠A＝∠BCD＝30°，AC＝2.‎ 设AD＝x(0＜x＜2)，则CD＝2－x.‎ ‎∴S△BCD＝BC·CD·sin 30°＝(2－x)．‎ 在△ABD中，由余弦定理得BD＝.‎ ‎∵棱锥的高h等于A到BD的距离，S△ABD＝x，‎ ‎∴h＝＝.‎ ‎∴VPBCD＝S△BCD·h＝·.‎ 令t＝2x－x2，‎ ‎∵0＜x＜2，∴0＜t≤3，‎ ‎∴VPBCD＝·＝ ‎＝ ＝ .‎ ‎∵0＜t≤3，∴≥，∴当＝时，VPBCD有最大值.‎ ‎【答案】 ‎15．(2016·江苏)现需要设计一个仓库，它由上下两部分组成，上部分的形状是正四棱锥PA1B1C1D1，下部分的形状是正四棱柱ABCDA1B1C1D1(如图所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍．‎ ‎(1)若AB＝6 m，PO1＝2 m，则仓库的容积是多少？‎ ‎(2)若正四棱锥的侧棱长为6 m，则当PO1为多少时，仓库的容积最大？‎ ‎【解析】 (1)由PO1＝2知O1O＝4PO1＝8.‎ 因为A1B1＝AB＝6，所以正四棱锥PA1B1C1D1的体积V锥＝·A1B·PO1＝×62×2＝24(‎ m3)；‎ 正四棱柱ABCDA1B1C1D1的体积V柱＝AB2·O1O＝62×8＝288(m3)．‎ 所以仓库的容积V＝V锥＋V柱＝24＋288＝312(m3)．‎ ‎(2)设A1B1＝a(m)，PO1＝h(m)，‎ 则0＜h＜6，O1O＝4h.如图，连接O1B1.‎ 因为在Rt△PO1B1中，O1B＋PO＝PB，‎ 所以＋h2＝36，即a2＝2(36－h2)．‎ 于是仓库的容积V＝V柱＋V锥＝a2·4h＋a2·h＝a2h＝(36h－h3)，0＜h＜6，‎ 从而V′＝(36－3h2)＝26(12－h2)．‎ 令V′＝0，得h＝2或h＝－2(舍)．‎ 当0＜h＜2时，V′＞0，V是单调增函数，‎ 当2＜h＜6时，V′＜0，V是单调减函数．‎ 故当h＝2时，V取得极大值，也是最大值．‎ 因此，当PO1＝2 m时，仓库的容积最大．‎