高考文科数学复习备课课件：第二节　函数的单调性与最值 26页

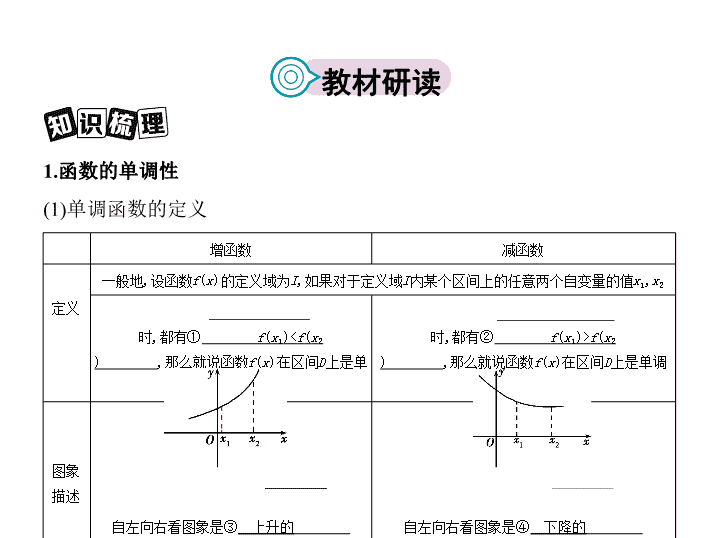
文数 课标版 第二节　函数的单调性与最值 1.函数的单调性 (1)单调函数的定义 教材研读 增函数 减函数 定义 一般地,设函数 f ( x )的定义域为 I ,如果对于定义域 I 内某个区间上的任意两个自变量的值 x 1 , x 2 当 x 1 < x 2 时,都有①      f ( x 1 )< f ( x 2 )     ,那么就说函数 f ( x )在区间 D 上是单调增函数 当 x 1 < x 2 时,都有②      f ( x 1 )> f ( x 2 )     ,那么就说函数 f ( x )在区间 D 上是单调减函数 图象描述   自左向右看图象是③ 　上升的       自左向右看图象是④ 　下降的     (2)单调区间的定义 若函数 f ( x )在区间 D 上是⑤ 　增函数     或⑥ 　减函数     ,则称函数 f ( x )在这一区间上具有(严格的)单调性,区间 D 叫做 y = f ( x )的单调区间. (3)判断函数单调性的方法 (i)定义法:利用定义判断. (ii)利用函数的性质:如,若 y = f ( x )、 y = g ( x )为增函数,则 a. y = f ( x )+ g ( x )为增函数; b. y =   为减函数( f ( x )>0); c. y =   为增函数( f ( x ) ≥ 0); d. y = f ( x )· g ( x )为增函数( f ( x )>0, g ( x )>0); e. y =- f ( x )为减函数. (iii)利用复合函数关系判断单调性 法则是“同增异减”,即:若两个简单函数的单调性相同,则这两个函数 的复合函数为增函数;若两个简单函数的单调性相反,则这两个函数的 复合函数为减函数. (iv)图象法 (v)导数法 2.函数的最值 前提 设函数 y = f ( x )的定义域为 I ,如果存在实数 M 满足 条件 (1)对于任意的 x ∈ I ,都有⑦      f ( x ) ≤ M      ; (2)存在 x 0 ∈ I ,使得⑧      f ( x 0 )= M      (1)对于任意的 x ∈ I ,都有⑨      f ( x ) ≥ M      ; (2)存在 x 0 ∈ I ,使得⑩      f ( x 0 )= M      结论 M 为函数 y = f ( x )的最大值 M 为函数 y = f ( x )的最小值   　　判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)在增函数与减函数的定义中,可以把“任意两个自变量”改为“存 在两个自变量”.   ( × ) (2)函数 y =   的单调递减区间是(- ∞ ,0) ∪ (0,+ ∞ ).   ( × ) (3)所有的单调函数都有最值.   ( × ) 1.下列函数中,在区间(0,1)上是增函数的是   (　　) A. y =| x |　    B. y =3- x C. y =   　    D. y =- x 2 +4 答案     A     y =3- x 在 R 上递减, y =   在(0,+ ∞ )上递减, y =- x 2 +4在(0,+ ∞ )上递 减,故选A. 2.函数 y = x 2 -6 x +10在区间(2,4)上   (　　) A.递减　    B.递增 C.先递减后递增　    D.先递增后递减 答案     C　∵函数 y = x 2 -6 x +10的图象为抛物线,且开口向上,对称轴为直 线 x =3, ∴函数 y = x 2 -6 x +10在(2,3)上为减函数,在(3,4)上为增函数. 3.若函数 y =(2 k +1) x + b 在 R 上是减函数,则 k 的取值范围是 　　　     . 答案        解析　 因为函数 y =(2 k +1) x + b 在 R 上是减函数,所以2 k +1<0,即 k <-   . 4.若函数 f ( x )满足“对任意的 x 1 , x 2 ∈ R ,当 x 1 < x 2 时,都有 f ( x 1 )> f ( x 2 )”,则满足 f (2 x -1)< f (1)的实数 x 的取值范围为      . 答案 　(1,+ ∞ ) 解析 　由题意知,函数 f ( x )在定义域内为减函数, ∵ f (2 x -1)< f (1),∴2 x -1>1, 即 x >1,∴ x 的取值范围为(1,+ ∞ ). 5.已知 f ( x )=   , x ∈[2,6],则 f ( x )的最大值为 　　　     ,最小值为 　　　     . 答案 　2;   解析　 易知函数 f ( x )=   在 x ∈[2,6]上为减函数,故 f ( x ) max = f (2)=2, f ( x ) min = f (6)=   . 考点一　函数单调性的判断 典例1 　(1)函数 y =   的单调递增区间为      , 单调递减区间为 　　　　　　     . (2)判断函数 f ( x )=   ( a >0)在 x ∈(-1,1)上的单调性. 答案 　(1)[2,+ ∞ );(- ∞ ,-3] 解析 　(1)令 u = x 2 + x -6, 则 y =   可以看作是由 y =   与 u = x 2 + x -6复合而成的函数. 令 u = x 2 + x -6 ≥ 0,得 x ≤ -3或 x ≥ 2. 易知 u = x 2 + x -6在(- ∞ ,-3]上是减函数,在[2,+ ∞ )上是增函数,而 y =   在[0, + ∞ )上是增函数, ∴ y =   的单调减区间为(- ∞ ,-3],单调增区间为[2,+ ∞ ). 考点突破 (2)任取 x 1 , x 2 ,满足-1< x 1 < x 2 <1, 则 f ( x 1 )- f ( x 2 )=   -   =   =   . ∵-1< x 1 < x 2 <1, ∴ x 2 - x 1 >0, x 1 x 2 +1>0,(   -1)(   -1)>0. 又∵ a >0,∴ f ( x 1 )- f ( x 2 )>0, 即 f ( x 1 )> f ( x 2 ), ∴函数 f ( x )在(-1,1)上为减函数. 易错警示 1.利用定义判断函数单调性的步骤 取值→作差→变形→确定符号→得出结论 注意:函数的单调性是函数在某个区间上的“整体”性质,所以不能仅 仅根据某个区间内的两个特殊值 x 1 , x 2 对应的函数值的大小就判断函数 在该区间上的单调性,必须保证这两个值是该区间内的任意两个值. 2.函数的单调性与“区间”紧密相关,函数的单调区间是函数定义域的 子集,所以要求函数的单调区间,必须先求出函数的定义域. 3.由图象确定函数的单调区间需注意:图象不连续且有多个上升段(下 降段)的函数,其单调增(减)区间要分开写,用“和”或“,”连接,不能用 “ ∪ ”连接. 4.利用复合函数“同增异减”的原则时,需先确定相应各函数的单调性. 1-1 　下列四个函数中,在(0,+ ∞ )上为增函数的是   (　　) A. f ( x )=3- x 　    B. f ( x )= x 2 -3 x C. f ( x )=-   　    D. f ( x )=-| x | 答案     C     f ( x )=3- x 在(0,+ ∞ )上为减函数;当 x ∈   时, f ( x )= x 2 -3 x 为减 函数,当 x ∈   时, f ( x )= x 2 -3 x 为增函数; f ( x )=-   在(0,+ ∞ )上为增函 数; f ( x )=-| x |在(0,+ ∞ )上为减函数. 1-2     (2017黑龙江、吉林八校联考)已知函数 f ( x )是定义在R上的奇函 数,且 x >0时, f ( x )=log 2 ( x +1)+3 x ,则满足 f ( x )>-4的实数 x 的取值范围是(    　) A.(-2,2)　    B.(-1,1)　    C.(-1,+ ∞ )　    D.(1,+ ∞ ) 答案     C　∵ f ( x )为定义在R上的奇函数,∴ f (0)=0, 当 x <0时,- x >0, f (- x )=log 2 (- x +1)-3 x , f ( x )=- f (- x )=-log 2 (- x +1)+3 x ( x <0), 此时函数单调递增, f (-1)=-4. 当 x ≥ 0时,满足 f ( x )>-4; 当 x <0时,由 f ( x )>-4可得 f ( x )> f (-1), ∴ x >-1,∴-1< x <0. 综上所述, x >-1.故选C. 考点二　函数的最值(值域) 典例2 　(1)函数 y = x +   的最小值为 　　　     . (2)函数 y =   的值域为 　　　     . (3)函数 f ( x )=   的最大值为 　　　     . 答案 　(1)1　(2)   　(3)2 解析 　(1)解法一:令 t =   , 则 t ≥ 0,且 x = t 2 +1, ∴原函数变为 y = t 2 +1+ t , t ≥ 0. 配方得 y =   +   , 又∵ t ≥ 0,∴ y ≥   +   =1. 故函数 y = x +   的最小值为1. 解法二:因为函数 y = x 和 y =   在定义域内均为增函数,故函数 y = x +   在[1,+ ∞ )内为增函数,所以 y min =1. (2) y =   =   =2+   =2+   . ∵   +   ≥   , ∴2<2+   ≤ 2+   =   , 故函数的值域为   . (3)当 x ≥ 1时,函数 f ( x )=   为减函数, 所以 f ( x )在 x =1处取得最大值,为 f (1)=1; 当 x <1时,易知函数 f ( x )=- x 2 +2在 x =0处取得最大值,为 f (0)=2. 故函数 f ( x )的最大值为2. 方法技巧 求函数最值的五种常用方法 (1)单调性法:先确定函数的单调性,再由单调性求最值. (2)图象法:先作出函数的图象,再观察其最高点、最低点,求出最值. (3)基本不等式法:先对解析式变形,使之具备“一正二定三相等”的条 件后用基本不等式求出最值. (4)导数法:先求导,然后求出在给定区间上的极值,最后结合端点值,求出 最值. (5)换元法:对比较复杂的函数可通过换元转化为熟悉的函数,再用相应 的方法求最值. 2-1 　对于任意实数 a , b ,定义min{ a , b }=   函数 f ( x )=- x +3, g ( x )=log 2 x , 则函数 h ( x )=min{ f ( x ), g ( x )}的最大值是 　　　     . 答案 　1 解析 　依题意, h ( x )=   当0< x ≤ 2时, h ( x )=log 2 x 是增函数, 当 x >2时, h ( x )=3- x 是减函数, 则 h ( x ) max = h (2)=1. 2-2 　(1)求函数 y =   的值域. (2)已知-   < k <   ,求函数 y =   的值域. 解析 　(1)因为 y =   =   =-   +   , 因为   ≠ 0,所以 y ≠ -   , 所以函数 y =   的值域为   . (2) y =   =   =3-   ,因为-   < k <   ,所以1 ≤ k 2 +1<4,所以-3 ≤ -   <-   ,所以0 ≤ 3-   <   ,所以0 ≤ y <   .所以函数 y =   的值域为   . 考点三　函数单调性的应用 命题角度一　比较大小 典例3 　已知函数 f ( x )的图象关于直线 x =1对称,当 x 2 > x 1 >1时,[ f ( x 2 )- f ( x 1 )]( x 2 - x 1 )<0恒成立,设 a = f   , b = f (2), c = f (e),则 a , b , c 的大小关系为   (　　) A. c > a > b 　    B. c > b > a 　     C. a > c > b 　    D. b > a > c 答案     D 解析 　由 f ( x )的图象关于直线 x =1对称可得 f   = f   . 由当 x 2 > x 1 >1时,[ f ( x 2 )- f ( x 1 )]( x 2 - x 1 )<0恒成立,知 f ( x )在(1,+ ∞ )上单调递减. ∵1<2<   f   > f (e), 即 f (2)> f   > f (e), ∴ b > a > c . 3-1 　若函数 f ( x )= x 2 + a | x -2|在(0,+ ∞ )上单调递增,则实数 a 的取值范围是   (　　) A.[-4,0]　    B.[0,4]　     C.(- ∞ ,-4]　    D.[0,+ ∞ ) 答案     A　∵ f ( x )= x 2 + a | x -2|, ∴ f ( x )=   又∵ f ( x )在(0,+ ∞ )上单调递增, ∴   解得-4 ≤ a ≤ 0, 即实数 a 的取值范围是[-4,0]. 3-2 　已知函数 f ( x )= x 3 +3 x ,对任意的 m ∈[-2,2], f ( mx -2)+ f ( x )<0恒成立,则 实数 x 的取值范围是 　　　　　     . 答案        解析 　易知函数 f ( x )= x 3 +3 x 为奇函数, ∴ f ( mx -2)+ f ( x )<0可化为 f ( mx -2)< f (- x ), 又函数 f ( x )单调递增, ∴ mx -2<- x ,即 mx + x -2<0, ∴   ∴-2< x <   . 命题角度二　解不等式 典例4 　已知 f ( x )是定义在(0,+ ∞ )上的单调增函数,满足 f ( xy )= f ( x )+ f ( y ), f (3)=1,当 f ( x )+ f ( x -8) ≤ 2时, x 的取值范围是   (　　) A.(8,+ ∞ )　    B.(8,9]　     C.[8,9]　    D.(0,8) 答案     B 解析 　2=1+1= f (3)+ f (3)= f (9), 由题意及 f ( x )+ f ( x -8) ≤ 2, 可得 f [ x ( x -8)] ≤ f (9), 因为 f ( x )是定义在(0,+ ∞ )上的单调增函数, 所以有   解得8< x ≤ 9. 典例5 　已知函数 f ( x )=   满足对任意的实数 x 1 ≠ x 2 都有   <0成立,则实数 a 的取值范围为   (　　) A.(0,1)　    B.   　     C.   　    D.   答案     C 解析 　根据题意知函数 f ( x )在定义域R上为减函数,则   解得   ≤ a <   .故选C. 命题角度三　求参数 方法技巧 函数单调性应用的技巧 函数单调性的应用比较广泛,主要用来比较函数值的大小、解函数不等 式、求相关参数的范围、求函数的最值等. (1)比较两个函数值的大小 若 f ( x )在给定的区间 A 上是递增的,任取 x 1 , x 2 ∈ A ,则 x 1 < x 2 ⇔ f ( x 1 )< f ( x 2 );若 f ( x )在给定的区间 A 上是递减的,任取 x 1 , x 2 ∈ A ,则 x 1 < x 2 ⇔ f ( x 1 )> f ( x 2 ).若给定 的两个自变量在同一单调区间上,可直接比较大小,否则,要先根据奇偶 性或周期性把它们转化到同一单调区间上,再利用单调性比较大小. (2)利用函数单调性解函数不等式 解函数不等式的关键是利用函数的单调性去掉函数符号“ f ”,变函数 不等式为一般不等式.去掉“ f ”时,要注意 f ( x )的定义域的限制. (3)利用函数的单调性求参数的取值范围 依据函数单调性的定义,对给定区间内的任意两个不相等的自变量对应 的函数值作差(满足函数关系式的自变量必须在定义域内,这是一个容 易被忽视的问题),通过构造关于参数的不等式进行求解.在求抽象函数 中参数的范围时,往往是利用函数的单调性将符号“ f ”去掉,得到关于 参数的不等式. (4)利用函数的单调性求解函数的最值 步骤:①判断函数的单调性;②计算端点处的函数值;③确定最大值和最 小值.