高二数学学业水平测试试题新人教A版 12页

正视图 侧视图 俯视图 高二数学试题 注意事项： 1．本试题分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷为选择题，共 60 分；第Ⅱ卷为非选择题， 共 90 分，满分 150 分，考试时间为 120 分钟。 2．第Ⅰ卷共 2 页，12 个小题，每小题 5 分；每小题只有一个正确答案，请将选出的答 案标号（A、B、C、D）涂在答题卡上。 第Ⅰ卷（选择题 共 60 分） 一、选择题（本大题共 12 个小题，每小题 5 分，满分共 60 分，每小题只有一个正确答案） 1、已知全集 RU ，集合  2 4 0M x x   ，则 MCU  （ ） A  2 2x x   B  2 2x x   C  2 2x x x  或 D  2 2x x x  或 2、下面的抽样方法是简单随机抽样的是( ) A 在某年明信片销售活动中,规定每 100 万张为一个开奖组,通过随机抽取的方式确定号 码的后四位为 2709 为三等奖。 B 某车间包装一种产品,在自动的传送带上,每隔 5 分钟抽一包产品,称其重量是否合格 C 某校分别从行政,教师,后勤人员中抽取 2 人,14 人,4 人了解学校机构改革的意见。 D 用抽签法从 10 件产品中选取 3 件进行质量检验。 3、从装有 2 个红球和 2 个白球的口袋内任取 2 个,则互斥但不对立的两个事件是（ ） A 至少一个白球与都是白球 B 至少一个白球与至少一个红球 C 恰有一个白球与恰有 2 个白球 D 至少有 1 个白球与都是红球 4、在△ ABC 中，点 D 在 BC 边上，且 DBCD 2 ， ACsABrCD  ，则 sr  = （ ） A 3 2 B 3 4 C 3 D 0 5、函数 xxxf 2ln)(  的零点所在的大致区间是 ( ) A )2,1( B )3,2( C )1,1(e 和 )4,3( D ),( e 6、一个几何体的三视图如图，其中正视图中 △ ABC 是边长为 2 的正三角形，俯视图 为正六边形，则侧视图的面积为（ ） A 2 3 B 3 2 C 12 D 6 7、已知 nm, 是两条不重合的直线， ，  ， 是三个两两不重合的平面，给出下列四 个命题： ①若 , ,m m   则 //  ； ②若 , ,     则 //  ； ③若 , , // ,m n m n   则 //  ； ④若 nm, 是异面直线， , // , , // ,m m n n     则 //  ． 其中正确命题的个数是 ( ) A ①和④ B ①和③ C ③和④ D ①和② 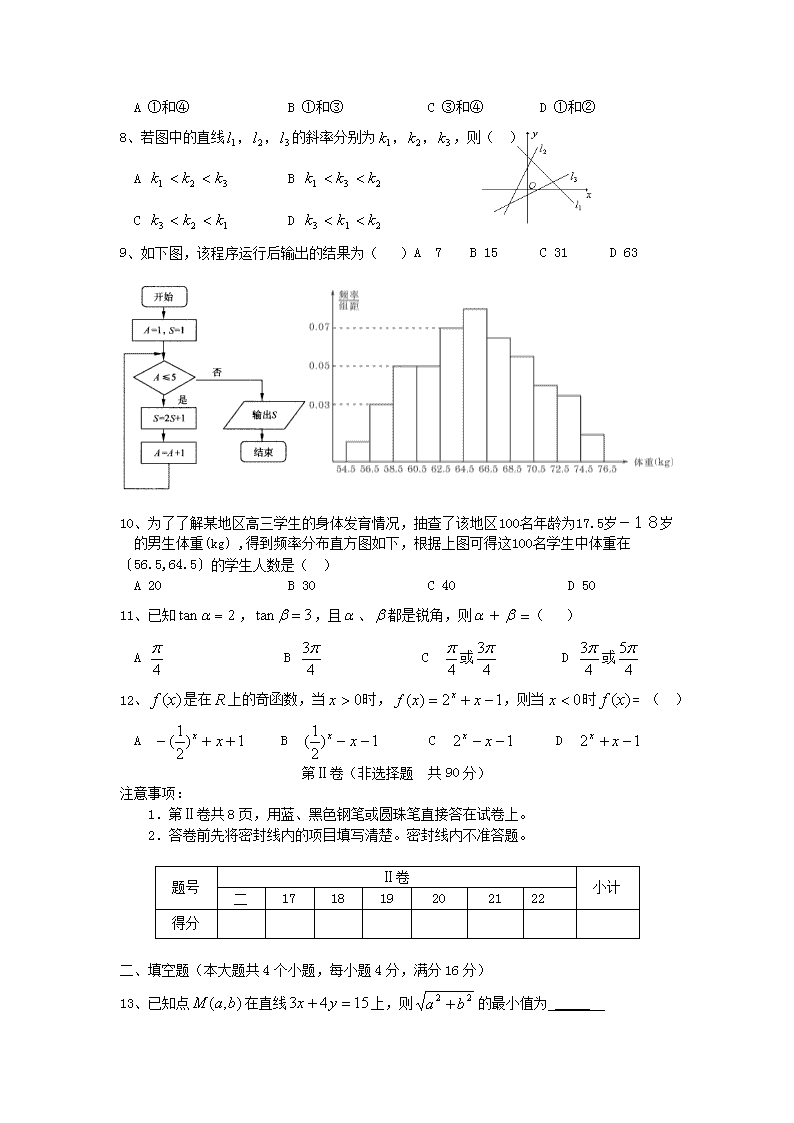8、若图中的直线 l l l1 2 3， ， 的斜率分别为 k k k1 2 3， ， ，则（ ） A k k k1 2 3  B k k k1 3 2  C k k k3 2 1  D k k k3 1 2  9、如下图，该程序运行后输出的结果为（ ）A 7 B 15 C 31 D 63 10、为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－１８岁 的男生体重(kg) ,得到频率分布直方图如下，根据上图可得这100名学生中体重在 〔56.5,64.5〕的学生人数是（ ） A 20 B 30 C 40 D 50 11、已知 tan 2  ， tan 3  ，且 、  都是锐角，则 ＋   （ ） A 4  B 4 3 C 4  或 4 3 D 4 3 或 4 5 12、 )(xf 是在 R 上的奇函数，当 0x 时， 12)(  xxf x ，则当 0x 时 )(xf = （ ） A 1)2 1(  xx B 1)2 1(  xx C 12  xx D 12  xx 第Ⅱ卷（非选择题 共 90 分） 注意事项： 1．第Ⅱ卷共 8 页，用蓝、黑色钢笔或圆珠笔直接答在试卷上。 2．答卷前先将密封线内的项目填写清楚。密封线内不准答题。 题号 Ⅱ卷 小计二 17 18 19 20 21 22 得分 二、填空题（本大题共 4 个小题，每小题 4 分，满分 16 分） 13、已知点 ),( baM 在直线 1543  yx 上，则 22 ba  的最小值为 _____ 14、一个正方体的各顶点均在同一球的球面上，若该球的体积为 34 ，则该正方体的 表面积为_________ 15、若以连续掷两次骰子分别得到的点数 nm, 作为点 P 的坐标，则点 P 落在圆 1622  yx 内的概率是 16、在下列结论中： ①函数 )4(2cos xy   是偶函数； ②函数 )32sin(4  xy 的一个对称中心是（ 6  ，0）； ③函数  3 2)32cos(  xxy 的图象的一条对称轴为 ； ④若 .5 1cos,2)tan( 2  xx 则 ⑤函数 xy 2sin 的图像向左平移 4  个单位，得到 )42sin(  xy 的图像 其中正确结论的序号为 三、解答题(本大题共 6 小题,共 74 分。解答应写出文字说明、证明过程或演算步骤) 17、（满分 12 分） 利用单调性的定义证明函数 1 2)(   x xxf 在 ),1(  上是减函数，并求函数 )(xf 在 ]1,0[ 上的最大值和最小值 18、（满分 12 分） 已知一圆与 y 轴相切，圆心在直线 03  yx 上，且被直线 xy  截得的弦长为 72 ， 求该圆的方程 19、（满分 12 分） 设有关于 x 的一元二次方程 02 22  baxx （1）若 a 是从 0，1，2，3 四个数中任意取一个数，b 是从 0，1，2 三个数中任意取一个， 求上述方程有实根的概率 （2）若 ]1,0[],2,0[  ba ，求上述方程有实根的概率 20、（满分 12 分） 已知 CBA ,, 三点的坐标分别为 )sin,(cos),3,0(),0,3( CBA ，其中 )2 3,2(   （1）若 |||| BCAC  ，求角 的值； （2）若   tan1 2sinsin21 2   ，求BCAC 的值。 21、（满分 12 分） 如图，在长方体 1111 DCBAABCD  中， 1 ADAB ， 21 AA ，M 为 1CC 的中点(1) 求异面直线 MA1 与 11DC 所成的角的正切值 (2)求证：平面 ABM 平面 MBA 11 (3)求三棱锥 MBAB 11 的体积 M B1 A1 D1 C1 B A D C 22、（满分 14 分） 已知函数 1cos2cossin32)( 2  xxxxf )( Rx  （1）求函数 )(xf 的最小正周期 （2）求函数 )(xf 在区间 ]2,0[  上的最大值与最小值 （3）若 5 6)( 0 xf ， ]2,4[0 x ，求 02cos x 的值 高二数学答案 一、选择题 1-5 CDCDB 6-10 AADDC 11-12 BD 二、填空题 13、3 14、24 15、 9 2 16、②③④ 三、解答题 17、证明：任取 ),1(, 21 xx ，且 21 xx  ，则 …………………………1 分 1 2 1 2)()( 2 2 1 1 21    x x x xxfxf )1)(1( 21 12   xx xx …………………………4 分 因为 211 xx  ，所以 012  xx ， 011 x ， 012 x 所以 0)()( 21  xfxf ，即 )()( 21 xfxf  …………………………7 分 所以函数 )(xf 在 ),1(  上是减函数。 …………………………8 分 解：因为函数 )(xf 在 ),1(  上是减函数，所以函数 )(xf 在 ]1,0[ 上是减函数。 所以当 0x 时，函数 )(xf 在 ]1,0[ 上的最大值是 2， 所以当 1x 时，函数 )(xf 在 ]1,0[ 上的最小值是 2 3 。 …………………………12 分 18、解：设圆心为 ),( ba ，因为圆心在直线 03  yx 上，所以 03  ba ，所以 ba 3 ， 所以圆心为 ),3( bb . …………………………2 分 因为圆与 y 轴相切，所以 |3| br  …………………………4 分 圆心 )3,( bb 到直线 0 yx 的距离为 ||2 2 |3| bbbd  …………………………6 分 设弦长为l ，因为 222 )2( rld  ，所以 222 9)7(2 bb  所以 12 b ，所以 1b ， …………………………8 分 所以       3 1 3 r b a ，或       3 1 3 r b a …………………………10 分 所求圆的方程是 9)1()3( 22  yx ，或 9)1()3( 22  yx ……………12 分 19、解：(1)试验的全部结果有： (0,0),(0,1),(0,2), (1,0),(1,1),( 1,2), (2,0),(2,1),(2,2), (3,0),(3,1),(3,2). 共 12 个基本事件。 …………………………2 分 记方程有实根为事件 A， 因为 044 22  ba ， 0,0  ba ，所以 ba  ， 事件 A 包含的结果有 (0,0) (1,0),(1,1), (2,0),(2,1),(2,2), (3,0),(3,1),(3,2). 共 9 个基本事件， 所以 4 3 12 9)( AP 。 …………………………6 分 (2)试验的全部结果构成的区域  10,20),(  baba ， 212 S …………………………8 分 记方程有实根为事件 A， 因为 044 22  ba ， 0,0  ba ，所以 ba  ， 事件 A 包含的结果构成的区域  bababaA  ,10,20),( ，即图中的阴影部分。 2 3112 12 AS ，所以 4 3 2 2 3 )(  S SAP A 。 …………………………12 分 20、解：(1) || AC  cos610)(sin)3(cos 22  ， || BC  sin610)3(sin)(cos 22  ， …………………………2 分 因为 |||| BCAC  ，所以  sincos  ，即 1tan  ， 因为 )2 3,2(   ，所以 4 5  。 …………………………4 分 (2)因为 1 BCAC ，所以   0)3sin,(cossin,3cos   ， 所以 0sin3sincos3cos 22   ， …………………………6 分 b 2O 1 a 所以 3 1cossin   ， 所以 9 1)cos(sin 2   ， 所以 9 8cossin2  ， …………………………8 分 所以      cos cossin cossin2sin2 tan1 2sinsin2 22    ， …………………………10 分 9 8cossin2   。 …………………………12 分 21、(1)证明：取 DD1 中点 N，连接 MN，NA1. 因为 NDMC 11 // ，且 NDMC 11  ，所以 11// DCMN 。所以 MNA1 是异面直线 MA1 与 11DC 所成的角或其补角 ……2 分 111  DCMN ， 21 NA ， 31 MA ， 因为 2 1 2 1 2 MANAMN  ，所以  901NMA ， 所以 21 2tan 1 1  MN NAMNA 。 ……4 分 (2)因为 11BA 平面 CCBB 11 ， BM 平面 CCBB 11 ，所以 11BABM  ， 因为 21  MBBM ， 21 BB ，所以 2 1 2 1 2 BBMBBM  ，所以 MBBM 1 ， 因为 1111 BMBBA  ，所以 BM 平面 MBA 11 ， 因为平面 BM ABM ，所以平面 ABM 平面 MBA 11 …………………………8 分 (3) 设三棱锥 MBAB 11 的体积为V ，则 MBASV 113 1   BM = 3 12212 1 3 1  , …………………………12 分 22、解： 1cos2cossin32)( 2  xxxxf M B1 A1 D1 C1 B A D C N )62sin(2)2cos2 12sin2 3(22cos2sin3  xxxxx ……4 分 (1)   2 2T ……………… ………………………… …………………………5 分 (2)因为 20  x ，所以 6 7 626   x ， 所以 1)62sin(2 1  x ， 所以函数 )(xf 在区间 ]2,0[  上的最大值是 2，最小值是-1 …………………………9 分 (3)因为 5 6)( 0 xf ，所以 5 6)62sin(2 0  x ， 5 3)62sin( 0  x 因为 ]2,4[0 x ，所以 ]6 7,3 2[62 0  x ，所以 5 4)62cos( 0  x ， 所以 ]6)62cos[(2cos 00   xx = 6sin)62sin(6cos)62cos( 00   xx 2 1 5 3 2 3 5 4  10 343  。 ………………………… …………………………14 分