高中数学人教a版必修4阶段质量检测（一） word版含解析 13页

阶段质量检测(一) (A 卷 学业水平达标) (时间：90 分钟，满分：120 分) 一、选择题(本大题共 10 小题，每小题 5 分，共 50 分) 1．在 0°～360°的范围内，与－510°终边相同的角是( ) A．330° B．210° C．150° D．30° 答案：B 2．若－π 2<α<0，则点 P(tan α，cos α)位于( ) A．第一象限 B．第二象限 C．第三象限 D．第四象限 答案：B 3．已知角α的始边与 x 轴的非负半轴重合，终边过点 P(sin 120°，cos 120°)，则α可以是 ( ) A．60° B．330° C．150° D．120° 答案：B 4．若 sin2θ＋2cos θ＝－2，则 cos θ＝( ) A．1 B.1 2 C．－1 2 D．－1 答案：D 5．函数 f(x)＝tan x＋π 4 的单调增区间为( ) A. kπ－π 2 ，kπ＋π 2 ，k∈Z B．(kπ，(k＋1)π)，k∈Z C. kπ－3π 4 ，kπ＋π 4 ，k∈Z D. kπ－π 4 ，kπ＋3π 4 ，k∈Z 答案：C 6．已知 sin π 4 ＋α ＝ 3 2 ，则 sin 3π 4 －α 的值为( ) A.1 2 B．－1 2 C. 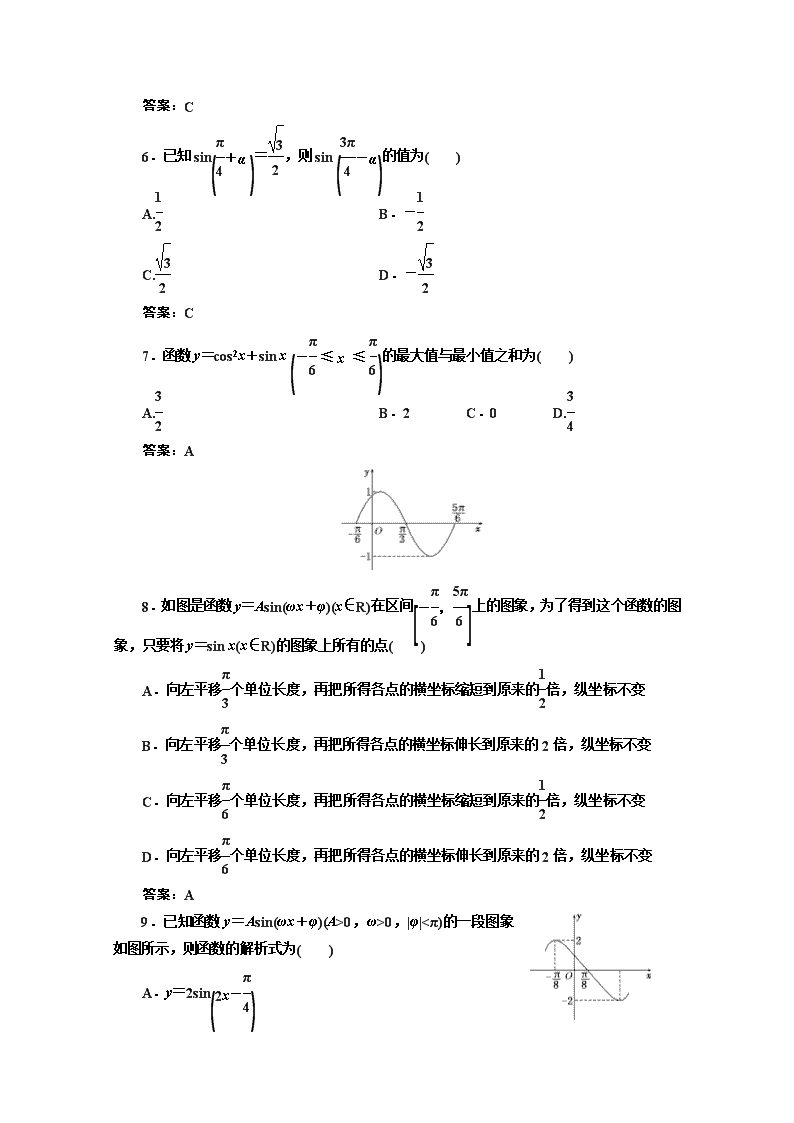3 2 D．－ 3 2 答案：C 7．函数 y＝cos2x＋sin x －π 6 ≤x≤π 6 的最大值与最小值之和为( ) A.3 2 B．2 C．0 D.3 4 答案：A 8．如图是函数 y＝Asin(ωx＋φ)(x∈R)在区间 －π 6 ，5π 6 上的图象，为了得到这个函数的图 象，只要将 y＝sin x(x∈R)的图象上所有的点( ) A．向左平移π 3 个单位长度，再把所得各点的横坐标缩短到原来的1 2 倍，纵坐标不变 B．向左平移π 3 个单位长度，再把所得各点的横坐标伸长到原来的 2 倍，纵坐标不变 C．向左平移π 6 个单位长度，再把所得各点的横坐标缩短到原来的1 2 倍，纵坐标不变 D．向左平移π 6 个单位长度，再把所得各点的横坐标伸长到原来的 2 倍，纵坐标不变 答案：A 9．已知函数 y＝Asin(ωx＋φ)(A>0，ω>0，|φ|<π)的一段图象如 图所示，则函数的解析式为( ) A．y＝2sin 2x－π 4 B．y＝2sin 2x－π 4 或 y＝2sin 2x＋3π 4 C．y＝2sin 2x＋3π 4 D．y＝2sin 2x－3π 4 答案：C 10．函数 f(x)＝Asin ωx(ω>0)，对任意 x 有 f x－1 2 ＝f x＋1 2 ，且 f －1 4 ＝－a，那么 f 9 4 等于( ) A．a B．2a C．3a D．4a 答案：A 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分) 11．已知 sin(π－α)＝－2 3 ，且α∈ －π 2 ，0 ，则 tan(2π－α)＝________. 解析：sin(π－α)＝sin α＝－2 3 ， ∵α∈ －π 2 ，0 ， ∴cos α＝ 1－sin2α＝ 5 3 ，tan(2π－α)＝－tan α＝－sin α cos α ＝2 5 5 . 答案：2 5 5 12．已知 sin θ＋cos θ＝4 3 0＜θ＜π 4 ，则 sin θ－cos θ的值为________． 解析：∵sin θ＋cos θ＝4 3 ， ∴(sin θ＋cos θ)2＝1＋2sin θcos θ＝16 9 ， ∴2sin θcos θ＝7 9.又 0＜θ＜π 4 ，∴sin θ＜cos θ. ∴sin θ－cos θ＝－ sin θ－cos θ2 ＝－ 1－2sin θcos θ＝－ 2 3 . 答案：－ 2 3 13．定义运算 a*b 为 a*b＝ aa≤b， ba>b， 例如 1] . 解析：由题意可知，这实际上是一个取小的自定义函数，结合函数的图象可得其值域为 －1， 2 2 . 答案： －1， 2 2 14．已知函数 f(x)＝Atan(ωx＋φ)ω＞0，|φ|＜π 2 ，y＝f(x)的部分图象如 图，则 f π 24 ＝________. 解析：由图象可知，此正切函数的半周期等于3π 8 －π 8 ＝2π 8 ＝π 4 ，即周期为π 2 ，所以ω＝2.由 题意可知，图象过定点 3π 8 ，0 ，所以 0＝Atan 2×3π 8 ＋φ ， 即3π 4 ＋φ＝kπ(k∈Z)，所以φ＝kπ－3π 4 (k∈Z)， 又|φ|＜π 2 ，所以φ＝π 4.再由图象过定点(0,1)， 所以 A＝1.综上可知 f(x)＝tan 2x＋π 4 . 故有 f π 24 ＝tan 2× π 24 ＋π 4 ＝tan π 3 ＝ 3. 答案： 3 三、解答题(本大题共 4 小题，共 50 分．解答时应写出文字说明、证明过程或演算步骤) 15．(本小题满分 12 分)已知 tan α tan α－1 ＝－1，求下列各式的值： (1)sin α－3cos α sin α＋cos α ； (2)sin2α＋sin αcos α＋2. 解：由 tan α tan α－1 ＝－1，得 tan α＝1 2. (1)sin α－3cos α sin α＋cos α ＝tan α－3 tan α＋1 ＝ 1 2 －3 1 2 ＋1 ＝－5 3. (2)sin2α＋sin αcos α＋2 ＝sin2α＋sin αcos α＋2(cos2α＋sin2α) ＝3sin2α＋sin αcos α＋2cos2α sin2α＋cos2α ＝3tan2α＋tan α＋2 tan2α＋1 ＝ 3 1 2 2＋1 2 ＋2 1 2 2＋1 ＝13 5 . 16．(本小题满分 12 分)已知α是第二象限角， 且 f(α)＝sin α－π 2 cos 3π 2 ＋α tanπ－α tan－α－πsin－π－α . (1)化简 f(α)； (2)若 cos α＋3π 2 ＝3 5 ，求 f(α)的值． 解：(1)f(α)＝－cos αsin α－tan α －tan αsin α ＝－cos α. (2)∵cos α＋3π 2 ＝sin α＝3 5 ， ∴sin α＝3 5.又∵α是第二象限角， ∴cos α＝－ 1－ 3 5 2＝－4 5. ∴f(α)＝－ －4 5 ＝4 5. 17．(本小题满分 12 分)已知函数 f(x)＝Asin(ωx＋φ)A>0，ω>0，|φ|<π 2 的图象在 y 轴上的截 距为 1，它在 y 轴右侧的第一个最大值点和最小值点分别为(x0,2)和(x0＋3π，－2)． (1)求 f(x)的解析式； (2)将 y＝f(x)的图象上所有点的横坐标缩短到原来的1 3 倍，纵坐标不变，然后再将所得的 图象沿 x 轴向右平移π 3 个单位长度，得到函数 y＝g(x)的图象，写出函数 y＝g(x)的解析式，并 用“五点法”作出 y＝g(x)在长度为一个周期的闭区间上的图象． 解：(1)∵f(x)＝Asin(ωx＋φ)在 y 轴上的截距为 1，最大值为 2，∴A＝2,1＝2sin φ，∴sin φ ＝1 2. 又∵|φ|<π 2 ，∴φ＝π 6. ∵两相邻的最大值点和最小值点分别为(x0,2)和(x0＋3π，－2)， ∴T＝2[(x0＋3π)－x0]＝6π， ∴ω＝2π T ＝2π 6π ＝1 3. ∴函数的解析式为 f(x)＝2sin x 3 ＋π 6 . (2)将 y＝f(x)的图象上所有点的横坐标缩短到原来的1 3 ，纵坐标不变，得函数的解析式为 y ＝2sin x＋π 6 ，再向右平移π 3 个单位后，得 g(x)＝2sin x－π 3 ＋π 6 ＝2sin x－π 6 . 列表如下： x－π 6 0 π 2 π 3π 2 2π x π 6 2π 3 7π 6 5π 3 13π 6 g(x) 0 2 0 －2 0 描点并连线，得 g(x)在一个周期的闭区间上的图象如下图． 18.( 本 小 题 满 分 14 分 ) 如 图 ， 函 数 y ＝ 2cos(ωx ＋ θ)x ∈ R ， ω>0,0≤θ≤π 2 的图象与 y 轴交于点(0， 3)，且该函数的最小正周期为π. (1)求θ和ω的值； (2)已知点 A π 2 ，0 ，点 P 是该函数图象上一点，点 Q(x0，y0)是 PA 的中点，当 y0＝ 3 2 ，x0∈ π 2 ，π 时，求 x0 的值． 解：(1)把(0， 3)代入 y＝2cos(ωx＋θ)中， 得 cos θ＝ 3 2 . ∵0≤θ≤π 2 ，∴θ＝π 6. ∵T＝π，且ω>0， ∴ω＝2π T ＝2π π ＝2. (2)∵点 A π 2 ，0 ，Q(x0，y0)是 PA 的中点，y0＝ 3 2 ， ∴点 P 的坐标为 2x0－π 2 ， 3 . ∵点 P 在 y＝2cos 2x＋π 6 的图象上， 且π 2 ≤x0≤π， ∴cos 4x0－5π 6 ＝ 3 2 ，且7π 6 ≤4x0－5π 6 ≤19π 6 . ∴4x0－5π 6 ＝11π 6 或 4x0－5π 6 ＝13π 6 . ∴x0＝2π 3 或 x0＝3π 4 . (B 卷 能力素养提升) (时间：90 分钟，满分：120 分) 一、选择题(本大题共 10 小题，每小题 5 分，共 50 分) 1．已知 cos θ tan θ<0，那么角θ是( ) A．第一或第二象限象 B．第二或第三象限角 C．第三或第四象限角 D．第一或第四象限角 解析：选 C 若 cos θtan θ<0， 则 cos θ>0，tan θ<0，或 cos θ<0，tan θ>0. 当 cos θ>0，tan θ<0 时，角θ是第四象限角； 当 cos θ<0，tan θ>0 时，角θ是第三象限角． 2．(陕西高考)函数 f(x)＝cos 2x－π 6 的最小正周期是( ) A.π 2 B．π C．2π D．4π 解析：选 B ∵T＝2π |ω| ＝2π 2 ＝π，∴B 正确． 3．函数 y＝cos x·tan x 的值域是( ) A．(－1,0)∪(0,1) B．[－1,1] C．(－1,1) D．[－1,0]∪(0,1) 解析：选 C 化简得 y＝sin x，由 cos x≠0，得 sin x≠±1.故得函数的值域(－1,1)． 4．圆的半径变为原来的 2 倍，而弧长也增加到原来的 2 倍，则( ) A．扇形的面积不变 B．扇形的圆心角不变 C．扇形的面积增大到原来的 2 倍 D．扇形的圆心角增大到原来的 2 倍 解析：选 B 根据弧度的定义可知：圆心角的大小等于弧长对半径的比，故选 B. 5．已知α＝5π 8 ，则点 P(sin α，tan α)所在的象限是( ) A．第一象限 B．第二象限 C．第三象限 D．第四象限 解析：选 D ∵π 2<5π 8 <π，∴sin α>0，tan α<0，∴点 P 在第四象限． 6．函数 y＝2sin 2x－π 6 的图象( ) A．关于原点成中心对称 B．关于 y 轴成轴对称 C．关于点 π 12 ，0 成中心对称 D．关于直线 x＝ π 12 成轴对称 解析：选 C 由形如 y＝Asin(ωx＋φ)函数图象的对称中心和对称轴的意义，分别将各选 项代入检验即可，由于 f π 12 ＝0，故函数的图象关于点 π 12 ，0 成中心对称． 7．函数 y＝tan x＋sin x－|tan x－sin x|在区间 π 2 ，3π 2 内的图象是( ) 解析：选 D 当π 2sin x，y＝2sin x．故选 D. 8．已知角α的终边上一点的坐标为 sinπ 6 ，cosπ 6 ，则角α的最小正值为( ) A.11π 6 B.5π 6 C.π 3 D.π 6 解析：选 C 由题意知，tan α＝ cos π 6 sinπ 6 ＝ 3. 所以α的最小正值为π 3. 9．函数 y＝cos π 4 －2x 的单调递增区间是( ) A. kπ＋π 8 ，kπ＋5π 8 B. kπ－3π 8 ，kπ＋π 8 C. 2kπ＋π 8 ，2kπ＋5π 8 D. 2kπ－3π 8 ，2kπ＋π 8 (以上 k∈Z) 解析：选 B 函数 y＝cosπ 4 －2x＝cos2x－π 4 ，根据余弦函数的增区间是[2kπ－π，2kπ]， k∈Z，得 2kπ－π≤2x－π 4 ≤2kπ，k∈Z，解得 kπ－3π 8 ≤x≤kπ＋π 8 ，k∈Z.故选 B. 10．函数 y＝3cos2x－4cos x＋1，x∈ π 3 ，2π 3 的最大值是( ) A.1 4 B.3 4 C.1 5 D.15 4 解析：选 D y＝3cos2x－4cos x＋1＝3 cos x－2 3 2－1 3.∵x∈ π 3 ，2π 3 ，∴cos x∈ －1 2 ，1 2 ， ∴当 cos x＝－1 2 ，即 x＝2π 3 时，ymax＝15 4 . 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分) 11．sin21°＋sin22°＋sin23°＋…＋sin288°＋sin289°＋sin290°的值为________． 解析：∵sin21°＋sin289°＝sin21°＋cos21°＝1， sin22°＋sin288°＝sin22°＋cos22°＝1， sin2x°＋sin2(90°－x°)＝sin2x°＋cos2x°＝1，(1≤x≤44，x∈N)， ∴原式＝(sin21°＋sin289°)＋(sin22°＋sin288°)＋…＋(sin244°＋sin246°)＋sin290°＋sin245° ＝45＋ 2 2 2＝91 2 . 答案：91 2 12．函数 y＝sin 2x 的图象向右平移φ个单位(φ>0)得到的图象恰好关于 x＝π 6 对称，则φ的 最小值是________． 解析：y＝sin 2x 向右平移φ个单位得 f(x)＝sin[2(x－φ)]＝sin(2x－2φ)． 由 f π 6 ＝sin π 3 －2φ ＝±1， ∴π 3 －2φ＝kπ＋π 2(k∈Z)， ∴2φ＝－kπ－π 6 ，令 k＝－1，得 2φ＝5π 6 ， ∴φ＝5π 12 或作出 y＝sin 2x 的图象观察易知φ＝π 6 － －π 4 ＝5π 12. 答案：5π 12 13．若 tan(π－α)＝2，则 2sin(3π＋α)·cos5π 2 ＋α＋sin 3 2π－α ·sin(π－α)的值为________． 解析：∵tan(π－α)＝2，∴tan α＝－2， ∴原式＝－2sin α·(－sin α)＋(－cos α)·sin α ＝2sin2α－sin αcos α＝2sin2α－sin αcos α sin2α＋cos2α ＝2tan2α－tan α 1＋tan2α ＝2×－22－－2 1＋－22 ＝10 5 ＝2. 答案：2 14．已知函数 y＝2sin(ωx＋θ)为偶函数(0<θ<π)，其图象与直线 y＝2 的交点的横坐标为 x1，x2，若|x1－x2|的最小值为π，则ω＝________，θ＝________. 解析：由已知 T＝π，∴ω＝2，θ＝kπ＋π 2(k∈Z)． 答案：2 π 2 三、解答题(本题共 4 小题，共 50 分．解答时应写出文字说明、证明过程或演算步骤) 15．(本小题满分 12 分)已知在△ABC 中，sin A＋cos A＝1 5. (1)求 sin Acos A； (2)判断△ABC 是锐角三角形还是钝角三角形； (3)求 tan A 的值． 解：(1)∵sin A＋cos A＝1 5 ①， ∴①式两边平方得 1＋2sin Acos A＝ 1 25 ， ∴sin Acos A＝－12 25. (2)由(1)sin Acos A＝－12 25 ，且 A∈(0，π)，可得 sin A>0，cos A<0，∴A 为钝角，∴△ABC 是钝角三角形． (3)∵(sin A－cos A)2＝1－2sin Acos A＝1＋24 25 ＝49 25 ，又 sin A>0，cos A<0， ∴sin A－cos A>0，∴sin A－cos A＝7 5 ②，∴由①，②可得 sin A＝4 5 ，cos A＝－3 5 ，∴tan A＝－4 3. 16．(本小题满分 12 分)已知函数 f(x)＝1＋ 2·sin2x－π 4. (1)求函数 f(x)的最小正周期和最大值； (2)画出函数 y＝f(x)在区间 －π 2 ，π 2 上的图象． 解：(1)函数 f(x)的最小正周期为 T＝2π 2 ＝π， 当 sin 2x－π 4 ＝1 时，f(x)取得最大值 1＋ 2. (2)由(1)知： x －π 2 －3π 8 －π 8 π 8 3π 8 π 2 y 2 1 1－ 2 1 1＋ 2 2 故函数 y＝f(x)在区间 －π 2 ，π 2 上的图象如图所示． 17．(本小题满分 12 分)设函数 f(x)＝3sinωx＋π 6 ，ω＞0，x∈(－∞，＋∞)，且以π 2 为最小 正周期． (1)求 f(0)； (2)求 f(x)的解析式； (3)已知 f α 4 ＋ π 12 ＝9 5 ，求 sinα的值． 解：(1)由题设可知 f(0)＝3sinπ 6 ＝3 2. (2)∵f(x)的最小正周期为π 2 ， ∴ω＝2π π 2 ＝4. ∴f(x)＝3sin 4x＋π 6 . (3)由 f α 4 ＋ π 12 ＝3sin α＋π 3 ＋π 6 ＝3cos α＝9 5 ， ∴cos α＝3 5. ∴sin α＝± 1－cos2α＝±4 5. 18．(本小题满分 14 分)已知函数 f(x)＝Asin(ωx＋φ)A>0，且ω>0,0<φ<π 2 的部分图象如图所 示． (1)求 A，ω，φ的值； (2)若方程 f(x)＝a 在 0，5π 3 上有两个不同的实根，试求 a 的取值范围． 解：(1)由图象易知 A＝1，函数 f(x)的周期为 T＝4× 7π 6 －2π 3 ＝2π，∴ω＝1. ∵π－2π 3 ＝π 3 ， ∴此函数的图象是由 y＝sin x 的图象沿 x 轴向左平移π 3 个单位长度得到的，故φ＝π 3. (2)由(1)知函数解析式为 f(x)＝sin x＋π 3 . ∴方程 f(x)＝a 在 0，5π 3 上有两个不同的实根等价于 y＝f(x)，x∈ 0，5 3π 与 y＝a 有两个 交点． 当 x＝0 时，f(x)＝ 3 2 ， ∴a∈ 3 2 ，1 时，y＝a 与 y＝f(x)有两个交点； 当 x＝5 3π时，f(x)＝0， ∴a∈(－1,0)时，y＝a 与 y＝f(x)也有两个交点， 故所求 a∈ 3 2 ，1 ∪(－1,0)．