2015年数学理高考课件10-5 古典概型 38页

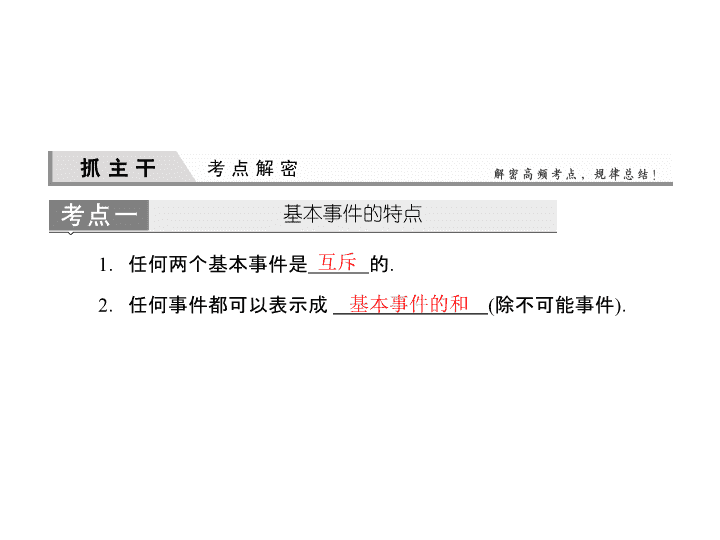
[ 最新考纲展示 ] 　 1 ． 理解古典概型及其概率计算公式．　 2. 会计算一些随机事件所含的基本事件数及事件发生的概率． 第五节　古典概型 基本事件的特点 1 ．任何两个基本事件是 的． 2 ．任何事件都可以表示成 ( 除不可能事件 ) ． 互斥 基本事件的和 古典概型的两个特点 1 ．试验中所有可能出现的基本事件只有 个，即 ． 2 ．每个基本事件发生的可能性 ，即 ． 提示： 确定一个试验为古典概型应抓住两个特征：有限性和等可能性． 有限 有限性 相等 等可能性 古典概型的概率公式 ____________________[ 通关方略 ]____________________ 　 古典概型中基本事件的探求方法 (1) 枚举法：适合给定的基本事件个数较少且易一一列举出的． (2) 树状图法：适合于较为复杂的问题中的基本事件的探求，注意在确定基本事件时 ( x ， y ) 可以看成是有序的，如 (1,2) 与 (2,1) 不同．有时也可以看成是无序的，如 (1,2)(2,1) 相同． (3) 排列组合法：在求一些较复杂的基本事件的个数时，可利用排列或组合的知识． 对于复杂的古典概型问题要注意转化为几个互斥事件概率问题去求． 1 ．从甲、乙、丙三人中任选两名代表，甲被选中的概率为 ( 　　 ) A. 　　　　 B. 　　　　 C. 　　　　 D ． 1 答案： C 答案： C 答案： D 4 ．在 20 瓶饮料中，有 2 瓶已过了保质期．从中任取 1 瓶，取到已过保质期的饮料的概率是 ________ ． 5 ． (2014 年南京模拟 ) 某单位从 4 名应聘者 A ， B ， C ， D 中招聘 2 人，如果这 4 名应聘者被录用的机会均等，则 A ， B 2 人中至少有 1 人被录用的概率是 ________ ． 基本事件及事件的构成 【 例 1】 　有两个正四面体的玩具，其四个面上分别标有数字 1,2,3,4 ，下面做投掷这两个正四面体玩具的试验：用 ( x ， y ) 表示结果，其中 x 表示第 1 个正四面体玩具出现的点数， y 表示第 2 个正四面体玩具出现的点数．试写出： (1) 试验的基本事件； (2) 事件 “ 出现点数之和大于 3 ” ； (3) 事件 “ 出现点数相等 ” ． [ 解析 ] 　 (1) 这个试验的基本事件为： (1,1) ， (1,2) ， (1,3) ， (1,4) ， (2,1) ， (2,2) ， (2,3) ， (2,4) ， (3,1) ， (3,2) ， (3,3) ， (3,4) ， (4,1) ， (4,2) ， (4,3) ， (4,4) ． (2) 事件 “ 出现点数之和大于 3 ” 包含以下 13 个基本事件： (1,3) ， (1,4) ， (2,2) ， (2,3) ， (2,4) ， (3,1) ， (3,2) ， (3,3) ， (3,4) ， (4,1) ， (4,2) ， (4,3) ， (4,4) ． (3) 事件 “ 出现点数相等 ” 包含以下 4 个基本事件： (1,1) ， (2,2) ， (3,3) ， (4,4) ． 反思总结 列举法可以使我们明确基本事件的构成情况，该法适用于基本事件的个数较少的情况．列举时要按规律分类列举，以避免重复或遗漏的情况出现． 变式训练 1 ．用红、黄、蓝三种不同颜色给图中 3 个矩形随机涂色，每个矩形只涂一种颜色，写出： (1) 试验的基本事件； (2) 事件 “ 3 个矩形颜色都相同 ” ； (3) 事件 “ 3 个矩形颜色都不同 ” ． 解析： (1) 所有可能的基本事件共 27 个． (2) 由图可知，事件 “ 3 个矩形都涂同一颜色 ” 包含以下 3 个基本事件：红红红，黄黄黄，蓝蓝蓝． (3) 由图可知，事件 “ 3 个矩形颜色都不同 ” 包含以下 6 个基本事件：红黄蓝，红蓝黄，黄红蓝，黄蓝红，蓝红黄，蓝黄红． 古典概型 【 例 2】 　 (2013 年高考辽宁卷 ) 现有 6 道题，其中 4 道甲类题， 2 道乙类题，张同学从中任取 2 道题解答．试求： (1) 所取的 2 道题都是甲类题的概率； (2) 所取的 2 道题不是同一类题的概率． 反思总结 计算古典概型事件的概率可分三步 (1) 算出基本事件的总个数 n ； (2) 求出事件 A 所包含的基本事件个数 m ； (3) 代入公式求出概率 P . 古典概型的综合应用 【 例 3】 　 (2014 年烟台一模 ) 某校从参加高三年级期中考试的学生中抽出 50 名学生，并统计了他们的数学成绩 ( 成绩均为整数且满分为 100 分 ) ，数学成绩分组及各组频数如下： [40,50) ， 2 ； [50,60) ， 3 ； [60,70) ， 14 ； [70,80) ， 15 ； [80,90) ， 12 ； [90,100) ， 4. (1) 请把给出的样本频率分布表中的空格都填上； (2) 估计成绩在 85 分以上学生的比例； (3) 为了帮助成绩差的学生提高数学成绩，学校决定成立 “ 二帮一 ” 小组，即从成绩 [90,100) 中选两位同学，共同帮助成绩在 [40,50) 中的某一位同学．已知甲同学的成绩为 42 分，乙同学的成绩为 95 分，求甲、乙两同学恰好被安排在同一小组的概率． 样本频率分布表 [ 解析 ] 　 (1) 样本的频率分布表： 反思总结 有关古典概型与统计结合的题型是高考考查概率的一个重要题型，已成为高考考查的热点，概率与统计结合题，无论是直接描述还是利用频率分布表、分布直方图、茎叶图等给出信息，只需要能够从题中提炼出需要的信息，则此类问题即可解决． 变式训练 2 ．某日用品按行业质量标准分成五个等级，等级系统 X 依次为 1,2,3,4,5. 现从一批该日用品中随机抽取 20 件，对其等级系数进行统计分析，得到频率分布表如下： (1) 若所抽取的 20 件日用品中，等级系统为 4 的恰有 3 件，等级系统为 5 的恰有 2 件，求 a ， b ， c 的值； (2) 在 (1) 的条件下，将等级系数为 4 的 3 件日用品记为 x 1 ， x 2 ， x 3 ，等级系统为 5 的 2 件日用品记为 y 1 ， y 2 ，现从 x 1 ， x 2 ， x 3 ， y 1 ， y 2 这 5 件日用品中任取两件 ( 假定每件日用品被取出的可能性相同 ) ，写出所有可能的结果，并求这两件日用品的等级系数恰好相等的概率． —— 古典概型的答题模板 从近两年的高考试题来看，古典概型是高考的热点，可在选择题、填空题中单独考查，也可在解答题中与统计等知识渗透综合考查，但题目一般不超过中等难度，以考查基本概念和基本运算为主，求解的关键在于正确计算随机试验不同的结果及事件 A 包含的基本事件数． 【 典例 】 　 (2013 年高考山东卷 )( 本题满分 12 分 ) 某小组共有 A ， B ， C ， D ， E 五位同学，他们的身高 ( 单位：米 ) 及体重指标 ( 单位：千克 / 米 2 ) 如下表所示： (1) 从该小组身高低于 1.80 的同学中任选 2 人，求选到的 2 人身高都在 1.78 以下的概率； (2) 从该小组同学中任选 2 个，求选到的 2 人的身高都在 1.70 以上且体重指标都在 [18.5,23.9) 中的概率． [ 教你快速规范审题 ] 1 ．审条件，挖解题信息 2 ．审结论，明解题方向 3 ．建联系，找解题突破口 1 ．审条件，挖解题信息 2 ．审结论，明解题方向 3 ．建联系，找解题突破口 [ 教你准确规范解答 ] (1) 从身高低于 1.80 的同学中任选 2 人，其一切可能的结果组成的基本事件有 ( A ， B ) ， ( A ， C ) ， ( A ， D ) ， ( B ， C ) ， ( B ， D ) ， ( C ， D ) ，共 6 个． 3 分 由于每个人被选到的机会均等，因此这些基本事件的出现是等可能的．选到的 2 人身高都在 1.78 以下的事件有 ( A ， B ) ， ( A ， C ) ， ( B ， C ) ，共 3 个．因此选到的 2 人身高都在 1.78 以下的概率为 P ＝＝ .6 分 (2) 从该小组同学中任选 2 人，其一切可能的结果组成的基本事件有 ( A ， B ) ， ( A ， C ) ， ( A ， D ) ， ( A ， E ) ， ( B ， C ) ， ( B ， D ) ， ( B ， E ) ， ( C ， D ) ， ( C ， E ) ， ( D ， E ) ，共 10 个． 9 分 由于每个人被选到的机会均等，因此这些基本事件的出现是等可能的．选到的 2 人身高都在 1.70 以上且体重指标都在 [18.5,23.9) 中的事件有 ( C ， D ) ， ( C ， E ) ， ( D ， E ) ，共 3 个． 因此选到的 2 人的身高都在 1.70 以上且体重指标都在 [18.5,23.9) 中的概率为 P 1 ＝ .12 分 [ 常见失分探因 ] 所求基本事件的结果数易出错 从 5 位同学选 2 人的基本事件注意有 10 种，易漏或重复 [ 教你一个万能模板 ] ―→ ―→ ―→ ―→ 本小节结束 请按 ESC 键返回