2019年高考数学练习题汇总小题提速练（三） 6页

小题提速练(三)‎ 一、选择题(本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．)‎ ‎1．已知集合A＝{x∈N|x≤6}，B＝{x∈R|x2－3x＞0}，则A∩B＝(　　)‎ A．{3，4，5，6}　　　　　 B．{x|3＜x≤6}‎ C．{4，5，6} D．{x|x＜0或3＜x≤6}‎ 解析：选C.依题意得A＝{0，1，2，3，4，5，6}，B＝{x|x＜0或x＞3}，因此A∩B＝{4，5，6}，选C.‎ ‎2．已知＝b＋2i(a，b∈R)，其中i为虚数单位，则a－b＝(　　)‎ A．－3 B．－2‎ C．－1 D．1‎ 解析：选A.依题意得1－ai＝b＋2i，因此a＝－2，b＝1，a－b＝－3，选A.‎ ‎3．某班有青年志愿者男生3人，女生2人，现需选出2名青年志愿者到社区做公益宣传活动，则选出的2名志愿者性别相同的概率为(　　)‎ A. B． C. D． 解析：选B.将3名男生记为M1，M2，M3，2名女生记为W1，W2，从这5名志愿者中选出2名的基本事件为(M1，M2)，(M1，M3)，(M1，W1)，(M1，W2)，(M2，M3)，(M2，W1)，(M2，W2)，(M3，W1)(M3，W2)，(W1，W2)，共有10种，其中所选的2名志愿者性别相同的基本事件为(M1，M2)，(M1，M3)，(M2，M3)，(W1，W2)，共有4种，因此选出的2名志愿者性别相同的概率为＝，选B.‎ ‎4．中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得至其关，要见次日行里数，请公仔细算相还．”其意思是有一个人走378里路，第一天健步行走，从第二天起脚痛，每天走的路程为前一天的一半，走了6天后到达目的地，请问第二天走了(　　)‎ A．96里 B．48里 C．192里 D．24里 解析：选A.依题意得，该人每天所走的路程依次排列形成一个公比为的等比数列．记为{an}，其前6项和等于378，于是有＝378，解得a1＝192，因此a2＝a1＝96‎ ‎，即该人第二天走了96里，选A.‎ ‎5．已知抛物线x2＝8y与双曲线－x2＝1(a＞0)的一个交点为M，F为抛物线的焦点，若|MF|＝5，则该双曲线的渐近线方程为(　　)‎ A．5x±3y＝0 B．3x±5y＝0‎ C．4x±5y＝0 D．5x±4y＝0‎ 解析：选B.设点M(x0，y0)，则有|MF|＝y0＋2＝5，y0＝3，x＝24，由点M(x0，y0)在双曲线－x2＝1上，得－x＝1，－24＝1，a2＝，所以双曲线－x2＝1的渐近线方程为－x2＝0，即3x±5y＝0，选B.‎ ‎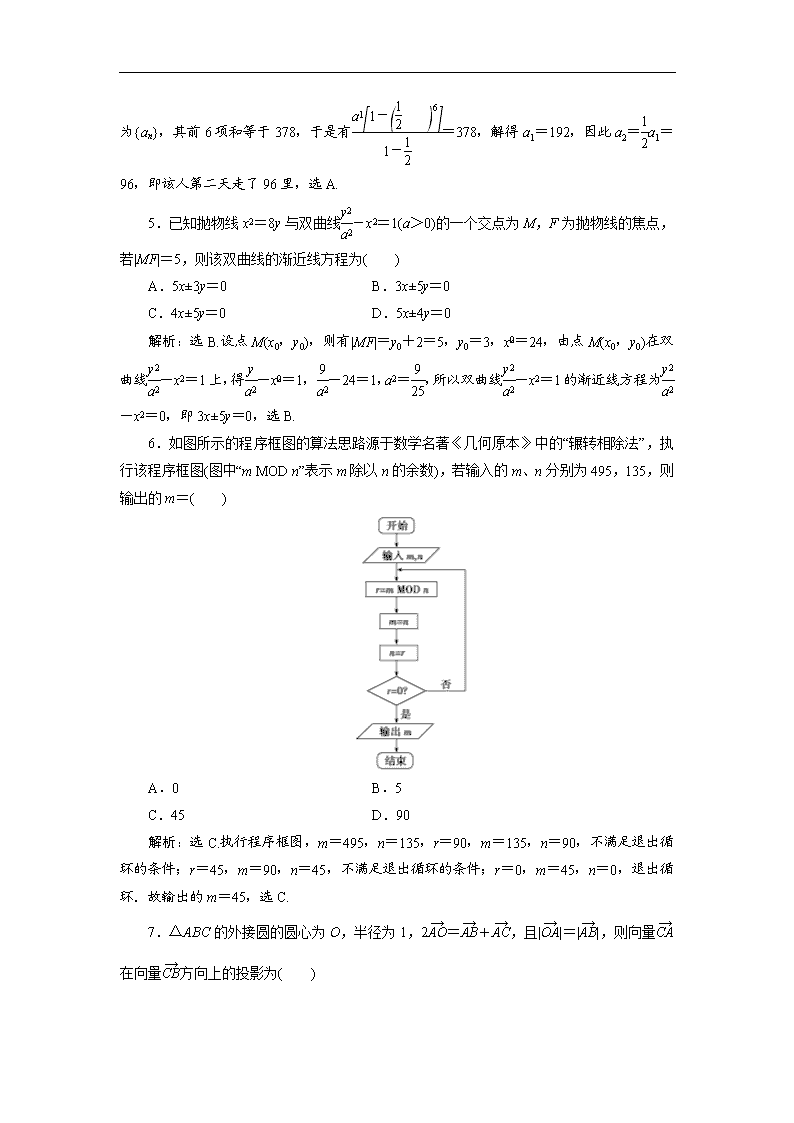6．如图所示的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图(图中“m MOD n”表示m除以n的余数)，若输入的m、n分别为495，135，则输出的m＝(　　)‎ A．0 B．5‎ C．45 D．90‎ 解析：选C.执行程序框图，m＝495，n＝135，r＝90，m＝135，n＝90，不满足退出循环的条件；r＝45，m＝90，n＝45，不满足退出循环的条件；r＝0，m＝45，n＝0，退出循环．故输出的m＝45，选C.‎ ‎7．△ABC的外接圆的圆心为O，半径为1，2＝＋，且||＝||，则向量在向量方向上的投影为(　　)‎ A. 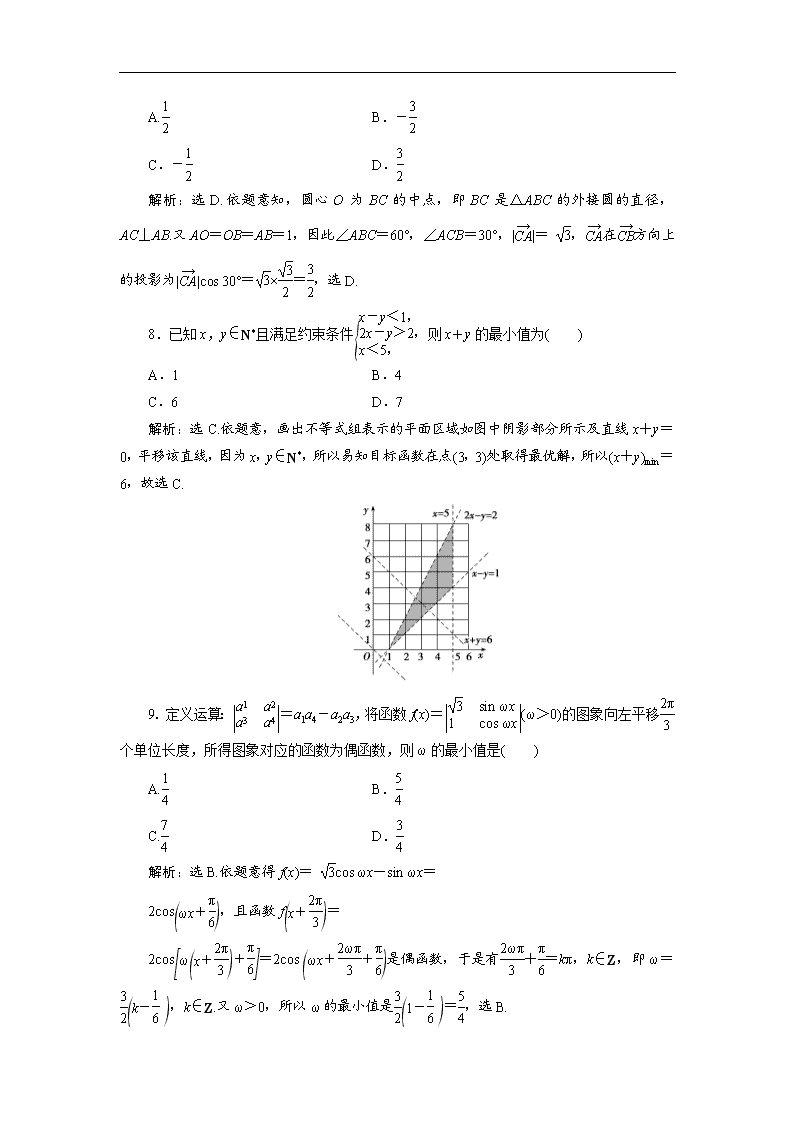B．－ C．－ D． 解析：选D.依题意知，圆心O为BC的中点，即BC是△ABC的外接圆的直径，AC⊥AB.又AO＝OB＝AB＝1，因此∠ABC＝60°，∠ACB＝30°，||＝ ，在方向上的投影为||cos 30°＝×＝，选D.‎ ‎8．已知x，y∈N*且满足约束条件则x＋y的最小值为(　　)‎ A．1 B．4‎ C．6 D．7‎ 解析：选C.依题意，画出不等式组表示的平面区域如图中阴影部分所示及直线x＋y＝0，平移该直线，因为x，y∈N*，所以易知目标函数在点(3，3)处取得最优解，所以(x＋y)min＝6，故选C.‎ ‎9．定义运算：＝a‎1a4－a‎2a3，将函数f(x)＝(ω＞0)的图象向左平移个单位长度，所得图象对应的函数为偶函数，则ω的最小值是(　　)‎ A. B． C. D． 解析：选B.依题意得f(x)＝ cos ωx－sin ωx＝‎ ‎2cos，且函数f＝‎ ‎2cos＝2cos是偶函数，于是有＋＝kπ，k∈Z，即ω＝，k∈Z.又ω＞0，所以ω的最小值是＝，选B.‎ ‎10．设曲线f(x)＝ cos x(m∈R)上任一点(x，y)处的切线斜率为g(x)，则函数y＝x‎2g(x)的部分图象可以为(　　)‎ 解析：选D.依题意得g(x)＝－ sin x，y＝x‎2g(x)＝－ x2sin x，易知函数y＝－ x2sin x是奇函数，其图象关于原点中心对称，故B，C均不正确，又当x∈时，y＝－ x2sin x＜0，故选D.‎ ‎11．某工件的三视图如图所示，现将该工件通过切削，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为(材料利用率＝)(　　)‎ A. B． C. D． 解析：选A.依题意知，题中的工件形状是一个底面半径为1、高为2的圆锥，设新工件的长、宽、高分别为a，b，c，截去的小圆锥的底面半径、高分别为r，h，则有a2＋b2＝4r2，h＝2r，该长方体的体积为abc＝ab(2－2r)≤＝4r2(1－r)．记f(r)＝4r2(1－r)，则有f′(r)＝4r(2－3r)，当0＜r＜时，f′(r)＞0，当＜r＜1时，f′(r)＜0，因此f(r)＝4r2(1－r)的最大值是f＝，则原工件材料的利用率为÷＝，选A.‎ ‎12．设函数f(x)＝若关于x的方程f(x)＝a有四个不同的解x1，x ‎2，x3，x4，且x1＜x2＜x3＜x4，则＋的取值范围是(　　)‎ A．(－3，＋∞) B．(－∞，3)‎ C．[－3，3) D．(－3，3]‎ 解析：选D.在坐标平面内画出函数y＝f(x)的大致图象如图所示，结合图象可知，当且仅当a∈(0，2]时，直线y＝a与函数y＝f(x)的图象有4个不同的交点，即方程f(x)＝a有四个不同的解，此时有x1＋x2＝－4，|log2x3|＝|log2x4|(0＜x3＜1＜x4≤4)，即有－log2x3＝log2x4，x3x4＝1，所以＋＝x4－(1＜x4≤4)，易知函数y＝x4－在区间(1，4]上是增函数，因此其值域是(－3，3]，选D.‎ 二、填空题(本题共4小题，每小题5分，共20分．)‎ ‎13．设函数f(x)＝ax2＋b(a≠0)，若f(x)dx＝‎3f(x0)，x0＞0，则x0＝________．‎ 解析：依题意得＝3(ax＋b)，即3ax＝‎9a(a≠0)，x＝3(x0＞0)，由此解得x0＝ .‎ 答案： ‎14．由数字2，0，1，7组成没有重复数字的四位偶数的个数为________．‎ 解析：根据所组成的没有重复数字的四位偶数的个位是否为0进行分类计数；第一类，个位是0时，满足题意的四位偶数的个数为A＝6；第二类，个位是2时，满足题意的四位偶数的个数为C·A＝4.由分类加法计数原理得，满足题意的四位偶数的个数为6＋4＝10.‎ 答案：10‎ ‎15．已知曲线y＝x＋ln x在点(1，1)处的切线为l.若l与曲线y＝ax2＋(a＋2)x＋1相切，则a＝________．‎ 解析：依题意得，y′＝2，切线l的方程为y－1＝2(x－1)，即y＝2x－1，由消去y得ax2＋(a＋2)x＋1＝2x－1，即ax2＋ax＋2＝0，Δ＝a2－‎8a＝0(a≠0)，解得a＝8(a＝0舍去)．‎ 答案：8‎ ‎16．已知F1，F2分别是椭圆＋＝1(a＞b＞0)的左、右焦点，P是椭圆上一点(‎ 异于左、右顶点)，过点P作∠F1PF2的角平分线交x轴于点M，若2|PM|2＝|PF1|·|PF2|，则该椭圆的离心率为________．‎ 解析：在△PF‎1F2中，由角平分线定理，得＝，即＝.由椭圆定义得＝⇒＝.同理＝.‎ 又在△PF‎1M和△PF‎2M中，由余弦定理得cos ∠F1MP＋cos ∠F2MP＝0.即＋＝0，‎ 即(|PM|2＋|F‎1M||F‎2M|)(|F‎1M|＋|F‎2M|)＝|PF1|2|F‎2M|＋|PF2|2|F‎1M|⇒×‎2c＝|PF1|2|PF2|＋|PF2|2|PF1|⇒c＝(|PF1|＋|PF2|)‎ 即1＋2e2＝2，‎ 解得e＝.‎ 答案：