2019年高考数学总复习检测第40讲　算法初步与程序框图 6页

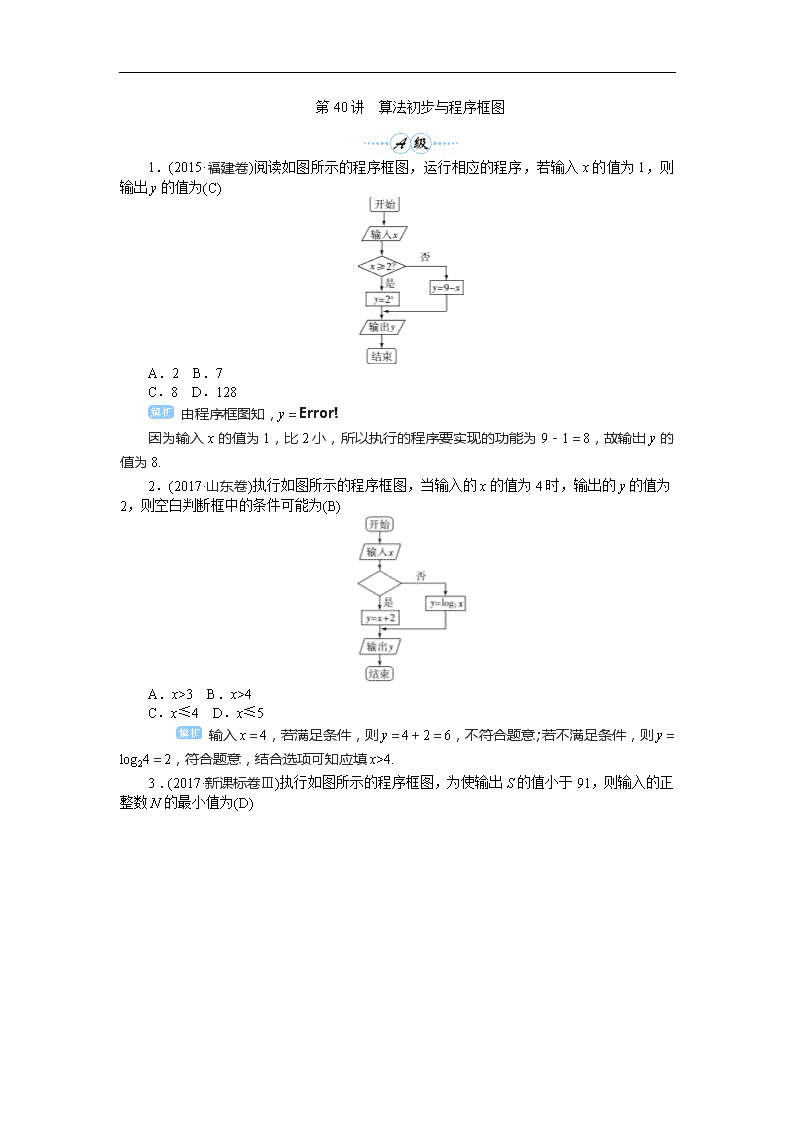
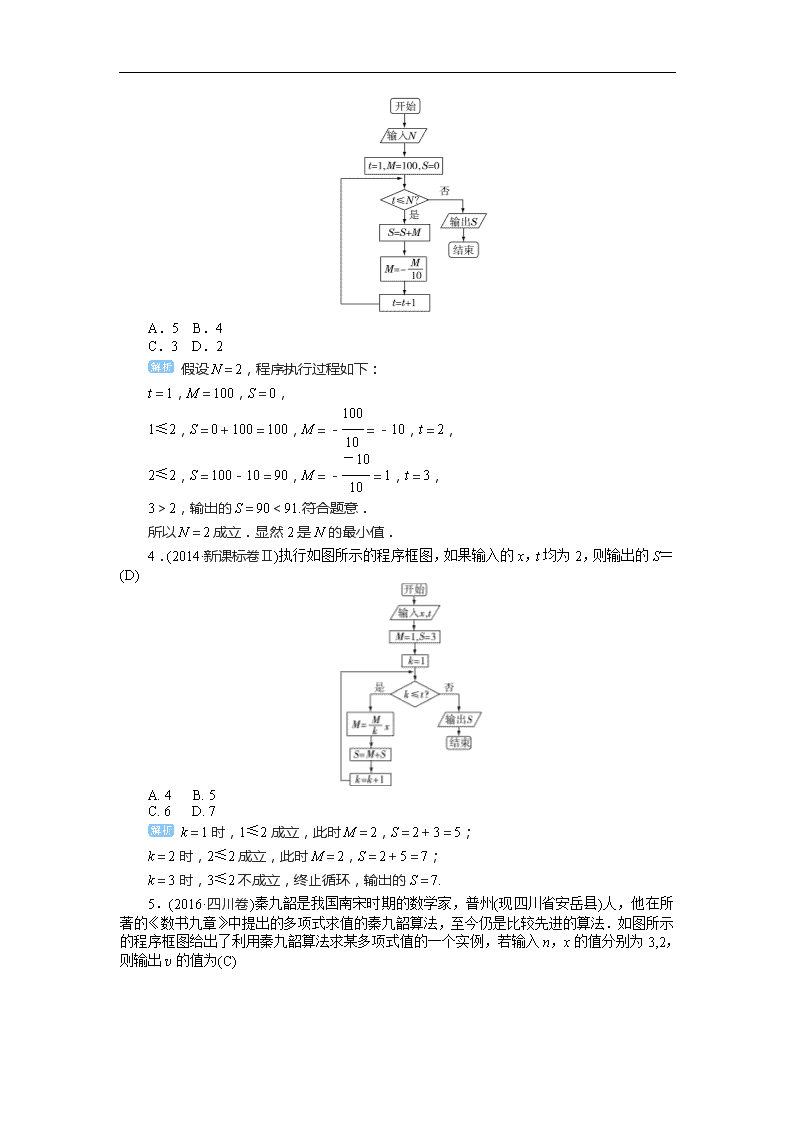
第40讲　算法初步与程序框图 ‎1．(2015·福建卷)阅读如图所示的程序框图，运行相应的程序，若输入x的值为1，则输出y的值为(C)‎ A．2 B．7‎ C．8 D．128‎ ‎ 由程序框图知，y＝ 因为输入x的值为1，比2小，所以执行的程序要实现的功能为9－1＝8，故输出y的值为8.‎ ‎2．(2017·山东卷)执行如图所示的程序框图，当输入的x的值为4时，输出的y的值为2，则空白判断框中的条件可能为(B)‎ A．x>3 B．x>4‎ C．x≤4 D．x≤5‎ ‎　　 输入x＝4，若满足条件，则y＝4＋2＝6，不符合题意；若不满足条件，则y＝log24＝2，符合题意，结合选项可知应填x>4.‎ ‎3．(2017·新课标卷Ⅲ)执行如图所示的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为(D)‎ A．5 B．4‎ C．3 D．2‎ ‎ 假设N＝2，程序执行过程如下：‎ t＝1，M＝100，S＝0，‎ ‎1≤2，S＝0＋100＝100，M＝－＝－10，t＝2，‎ ‎2≤2，S＝100－10＝90，M＝－＝1，t＝3，‎ ‎3＞2，输出的S＝90＜91.符合题意．‎ 所以N＝2成立．显然2是N的最小值．‎ ‎4．(2014·新课标卷Ⅱ)执行如图所示的程序框图，如果输入的x，t均为2，则输出的S＝(D)‎ A. 4 B. 5‎ C. 6 D. 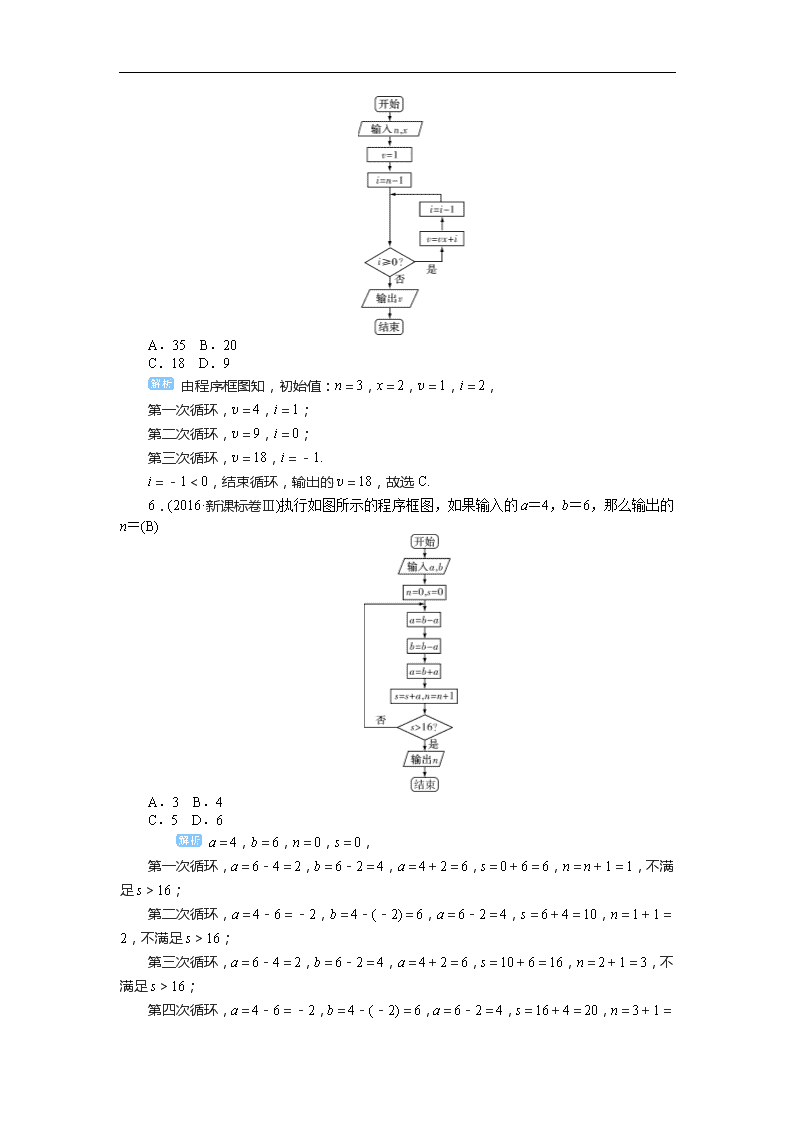7 ‎ ‎ k＝1时，1≤2成立，此时M＝2，S＝2＋3＝5；‎ k＝2时，2≤2成立，此时M＝2，S＝2＋5＝7；‎ k＝3时，3≤2不成立，终止循环，输出的S＝7.‎ ‎5．(2016·四川卷)秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n，x的值分别为3,2，则输出v的值为(C)‎ A．35 B．20‎ C．18 D．9‎ ‎ 由程序框图知，初始值：n＝3，x＝2，v＝1，i＝2，‎ 第一次循环，v＝4，i＝1；‎ 第二次循环，v＝9，i＝0；‎ 第三次循环，v＝18，i＝－1.‎ i＝－1＜0，结束循环，输出的v＝18，故选C.‎ ‎6．(2016·新课标卷Ⅲ)执行如图所示的程序框图，如果输入的a＝4，b＝6，那么输出的n＝(B)‎ A．3 B．4‎ C．5 D．6‎ ‎　　 a＝4，b＝6，n＝0，s＝0，‎ 第一次循环，a＝6－4＝2，b＝6－2＝4，a＝4＋2＝6，s＝0＋6＝6，n＝n＋1＝1，不满足s＞16；‎ 第二次循环，a＝4－6＝－2，b＝4－(－2)＝6，a＝6－2＝4，s＝6＋4＝10，n＝1＋1＝2，不满足s＞16；‎ 第三次循环，a＝6－4＝2，b＝6－2＝4，a＝4＋2＝6，s＝10＋6＝16，n＝2＋1＝3，不满足s＞16；‎ 第四次循环，a＝4－6＝－2，b＝4－(－2)＝6，a＝6－2＝4，s＝16＋4＝20，n＝3＋1＝4，满足s>16，输出的n＝4.‎ ‎7．(2017·新课标卷Ⅱ)执行如图所示的程序框图，如果输入的a＝－1，则输出的S＝(B)‎ A．2 B．3‎ C．4 D．5‎ ‎ 当K＝1时，S＝0＋(－1)×1＝－1，a＝1，执行K＝K＋1后，K＝2；‎ 当K＝2时，S＝－1＋1×2＝1，a＝－1，执行K＝K＋1后，K＝3；‎ 当K＝3时，S＝1＋(－1)×3＝－2，a＝1，执行K＝K＋1后，K＝4；‎ 当K＝4时，S＝－2＋1×4＝2，a＝－1，执行K＝K＋1后，K＝5；‎ 当K＝5时，S＝2＋(－1)×5＝－3，a＝1，执行K＝K＋1后，K＝6；‎ 当K＝6时，S＝－3＋1×6＝3，执行K＝K＋1后，K＝7>6，输出的S＝3.结束循环．‎ ‎8．(2017·新课标卷Ⅰ)如图所示的程序框图是为了求出满足3n－2n>1 000的最小偶数n，‎ 那么在和两个空白框中，可以分别填入(D)‎ A．A>1 000和n＝n＋1 B．A>1 000和n＝n＋2‎ C．A≤1 000和n＝n＋1 D．A≤1 000和n＝n＋2‎ ‎ 因为题目要求的是“满足3n－2n＞1 000的最小偶数n”，所以n的叠加值为2，所以内填入“n＝n＋2”．由程序框图知，当内的条件不满足时，输出n，所以内填入“A≤1 000”．故选D.‎ ‎9．(2018·华大新高考联盟教学质量测评)我国古代的劳动人民曾创造了灿烂的中华文化，戍边的官兵通过在烽火台上举火向国内报告，烽火台上点火表示数字1，不点火表示数字0.这蕴含了进位制的思想．如图所示的程序框图的算法思路就源于我国古代戍边官兵的“烽火传信”．执行该程序框图，若输入a＝110011，k＝2，n＝6，则输出b的值为(C)‎ A．19 B．31‎ C．51 D．63‎ ‎ 按照程序框图执行，b依次为0,1,3,3,3,19,51，故输出51.‎ ‎10．(2015·重庆卷)执行如图所示的程序框图，若输出k的值为8，则判断框内可填入的条件是(C)‎ A．s≤ B．s≤ C．s≤ D．s≤ ‎ 由s＝0，k＝0满足条件，则k＝2，s＝，满足条件；k＝4，s＝＋＝，满足条件；k＝6，s＝＋＝，满足条件；k＝8，s＝＋＝，不满足条件，输出的k＝8，所以应填s≤.‎ ‎11．(2016·天津卷)阅读下边的程序框图，运行相应的程序，则输出S的值为　4　.‎ ‎ 按照程序框图中的顺序依次计算，直到满足条件输出S的值．‎ 第一次，S＝8，n＝2；‎ 第二次，S＝2，n＝3；‎ 第三次，S＝4，n＝4，满足n>3，输出的S＝4.‎ ‎12．(2015·安徽卷)执行如图所示的程序框图(算法流程图)，输出的n为　4　.‎ ‎ 执行第一次判断：|a－1.414|＝0.414＞0.005，a＝，n＝2；‎ 执行第二次判断：|a－1.414|＝0.086＞0.005，a＝，n＝3；‎ 执行第三次判断：|a－1.414|＝0.014＞0.005，a＝，n＝4；‎ 执行第四次判断：|a－1.414|＜0.005，输出的n＝4.‎