八年级下数学课件《反比例函数的图像与性质》 (11)_苏科版 20页

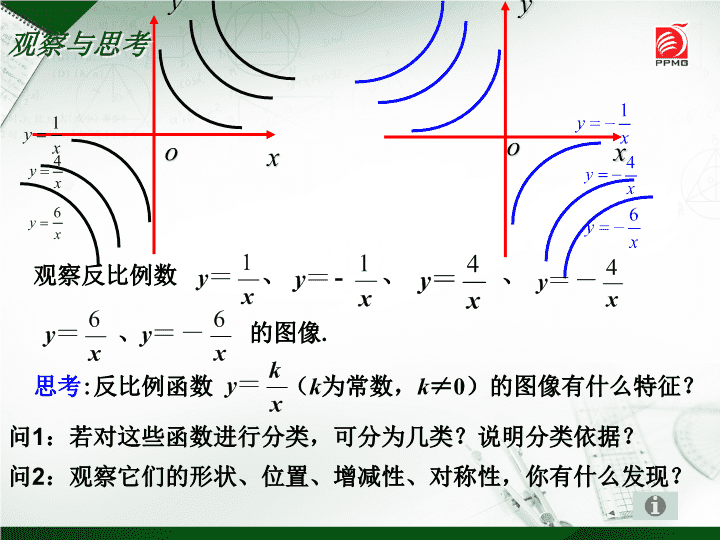
回顾与思考 1.下列关系式中y是x的反比例函数的是（　 　） A． B． C． D． x y 3 2  2 12  xy 4 xy  03 xy A 2. 反比例函数 图像是___________; 图像的两支分别在第_________ 象限． 反比例函数 的图象在第_______象限． 6y x  6y x   双曲线 一、三 二、四 八年级(下册)初中数学 11.2　反比例函数的图像与性质（2） y xo 1y x  1y x   4y x  4y x   6y x  6y x   观察反比例数 、 、 、 、 的图像. 4 ＝y x 4 ＝－y x 6 ＝y x 6 ＝－y x 1 ＝ -y x 1 ＝y x ＝ ky x思考:反比例函数 （k为常数，k≠0）的图像有什么特征？ 观察与思考 问2：观察它们的形状、位置、增减性、对称性，你有什么发现？ 问1：若对这些函数进行分类，可分为几类？说明分类依据？ 　　当k＜0时，双曲线的两支分别在_________象限， ______________，y随x的___________． 　　当k＞0时，双曲线的两支分别在________象限， ______________，y随x的___________； 反比例函数 （k为常数，k≠0）的图像是_______．＝ ky x 总结 11.2　反比例函数的图像与性质（2） k>0 k<0 双曲线 一、三 增大而减小在每一个象限内 二、四 在每一个象限内 增大而增大 探索 点A （4 ，－2 ）在函数 的图像上吗？ 写出点A关于原点O的对称点A′的坐标，点A′在 函数 的图像上吗？ 8y x ＝－ 在函数 的图像上任取一点B，点B关于原点O 的对称点B′在这个函数的图像上吗？ 11.2　反比例函数的图像与性质（2） 8y x ＝－ 8y x ＝－ 如果将反比例函数的图象绕原点旋转１８０度， 你有什么发现？ 反比例函数的两支图像关于原点对称． 探索 反比例函数图像是轴对称图形吗？ 如果是，对称轴有几条？ 形状 所在象限 增减性 对称性 ( 0)ky k x   通过对上述图象的观察，完成下列表格： ( 0)ky k x   双曲线 双曲线 一、三象限 在每一象限内 y随x的增大而减小 在每一象限内 y随x的增大而增大 既轴对称， 又中心对称 既轴对称， 又中心对称 二、四象限 1、函数 的图象在第_____象限，在每个 象限内，y 随 x 的增大而_____ . 3、函数 的图象在第二、四象限，则m的 取值范围是 ____ . 4、对于函数 ，当 x<0时，这部分图象在 第 _____象限，y 随x的增大而_____. 2.双曲线 经过点（-3， ） x y 5  x y 3 1  x my 2  x y 2 1  练习 学科网 1．反比例函数① ；② ；③ ； ④ 的图像中： （1）在第一、三象限的是 ，在 第二、四象限的是 . （2）在其所在的每一个象限内，y随x的增大而增大 的是 . 练习 2y x ＝ 1 3 y x ＝ 107 y x ＝－ 3 100 y x ＝ ① ② ④ ③ ③ 11.2　反比例函数的图像与性质（2） 例1　已知反比例函数 的图像经过点 A（2，－ 4）. （1）求k的值； （2）这个函数的图像在哪几个象限？y随x的 增大怎样变化？ ＝ ky x 11.2　反比例函数的图像与性质（2） （3）画出函数的图象； （4）点B（ ，－16）、C（ － 3，5）在这 个函数的图像上吗？ 1 2 画出函数的图象； 例2 若点（-2，y1）、（-1，y2）（1，y3）都 在反比例函数y = 的图象上， 则下列结论正确的是（ ） x 4 A. y1>y2>y3 B. y2>y1>y3 C. y3>y1>y2 D. y3>y2>y1 B 2 1m x   练习： 1.反比例函数 的图象如图所示，以下结论正 确的是 ____________ (填序号) ① 常数m ＜0； ② 在每个象限内，y随x的增大而增大； ③ 若A（－1，h），B（2，k）在图象上，则h＜k ④ 若P（x，y）在图象上，则P′（－x，－y）也在 图象上. my x  ③ ④ 2.已知反比例函数　　　 的图象上有两点 A（x1，y1)，B（x2，y2），且x1＜x2， 那么下列结论中，正确的是（　　 ） A. y1 y2 C. y1 =y2 D. y1 与y2之间的大小关系不能确定 x 1y   D 函数 与 y=x 的图象有交点， （1）求k的取值范围____________; （2） 若一个交点A的坐标是（－3，－3）， 请直接写出两个图象的另一个交点B的坐标. ky x  思考： 学科网 课堂小结： 谈谈你这一节课有哪些收获． 11.2　反比例函数的图像与性质（2） 2.一次函数y=kx－k 与反比例函数 y= 在同一直 角坐标系内的图象大致是（ ） x k D 5．已知反比例函数的图像经过点A（ － 6，－3）. （1）确定这个反比例函数的表达式； （2）这个函数的图像在哪几个象限？y随x的增大怎 样变化？ （3）点B（4， ），C（2，－5）在这个函数的 图像上吗？ 练习 9 2 11.2　反比例函数的图像与性质（2）