八年级下数学课件《6-1菱形的性质与判定》第3课时_鲁教版 20页

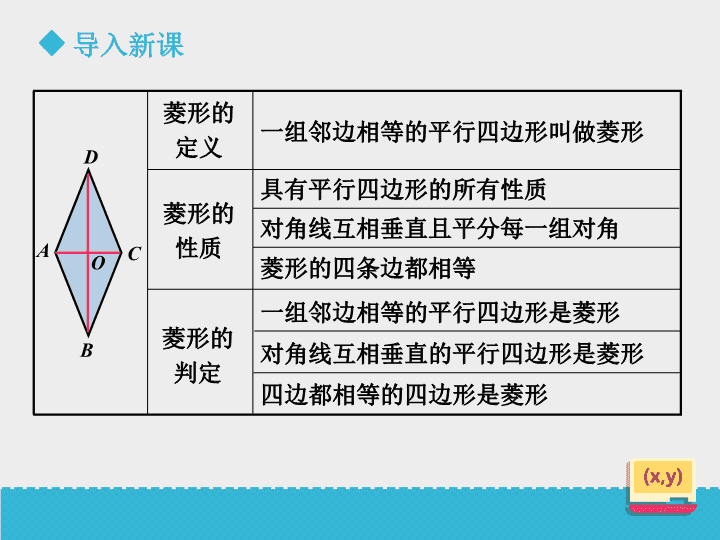
一组邻边相等的平行四边形叫做菱形　 具有平行四边形的所有性质 对角线互相垂直且平分每一组对角　 菱形的四条边都相等　 菱形的 定义 菱形的 性质 菱形的 判定 C　 D　 A　 B　 O　 一组邻边相等的平行四边形是菱形 对角线互相垂直的平行四边形是菱形 四边都相等的四边形是菱形 导入新课 导入新课 平行四边形的面积=底×高 菱形的面积怎样计算？ 导入新课 新课学习 例3 如图，四边形ABCD是边长 为13cm的菱形，其中对角线BD长10cm， 求：（1）对角线AC的长度； （2）菱形ABCD的面积. A B C D E 解：（1）∵四边形ABCD是菱形，AC与BD相交于点E， ∴∠AED=90°（菱形的对角线互相垂直） DE= BD= ×10=5(cm)(菱形的对角线互相平分) ∴ ∴AC=2AE=2×12=24(cm)(菱形的对角线互相平分) 1 2 1 2 2 2 2 2AE= AD DE = 13 5 =12(cm)  新课学习 例3 如图，四边形ABCD是边长 为13cm的菱形，其中对角线BD长10cm， 求：（1）对角线AC的长度； （2）菱形ABCD的面积. A B C D E 解：（2）菱形ABCD的面积 =△ABD的面积+△CBD的面积 =2×△ABD的面积 =2× ×BD×AE =2× ×10×12 =120(cm²) 1 2 1 2 新课学习 A B C D E 由第（2）小题可以看出： 菱形ABCD的面积 =2× ×BD×AE = ×BD×(2×AE) = ×BD×AC 1 2 1 2 1 2 菱形的面积=底×高= 对角线的乘积 1 2 把两张等宽的纸条交叉重叠在一起，你能 判断重叠部分ABCD的形状吗？ A C D B 新课学习 做一做 重叠部分ABCD是菱形。 D CB A E F 新课学习 证明：∵纸条等宽， ∴AB∥CD，AD∥BC，AE=AF ∴四边形ABCD是平行四边形 ∴∠ABC =∠ADC， 作AE⊥BC，AF⊥CD， ∴∠AEB=∠AFD=90° ∴△ABE≌△ADF ∴AB=AD ∴平行四边形ABCD是菱形 （邻边相等的平行四边形是菱形） 结论总结 菱形的面积= 对角线的乘积 1 2 菱形作为特殊的平行四边形， 面积=底×高。 课堂练习 1、菱形ABCD的周长为40cm，它的一条对角线长10cm. （1）求菱形的每一个内角的度数； A B C DO 解：（1）∵菱形ABCD的周长为40cm， ∴菱形的边长为40÷4=10（cm） ∴AB=AD=10cm， ∵BD=10cm， ∴△ABD是等边三角形， ∴∠BAD=60°， ∴∠ABC=180°-∠BAD=180°-60°=120°， ∴菱形的内角度数分别为： ∠BAD=∠BCD=60°，∠ABC=∠ADC=120°。 课堂练习 1、菱形ABCD的周长为40cm，它的一条对角线长10cm. （2）求菱形另一条对角线的长. A B C DO 解：（2）在菱形ABCD中， ∵对角线AC和BD互相垂直且平分， ∴BO= BD= ×10=5（cm） ∴在直角△AOB中， ∴AC=2AO=2× = （cm） 1 2 1 2  2 2 2 2AO= AB BO = 10 5 =5 3 cm  5 3 10 3 课堂练习 2、已知：如图，在Rt△ABC中，∠ACB=90°， ∠BAC=60°，BC的垂直平分线分别交BC和AB于点D、E， 点F在DE的延长线上，且AF=CE. 求证：四边形ACEF是菱形. A B C D E F证明：∵DE是BC的垂直平分线， ∴D是BD中点，∠EDC=90°， ∵∠ACB=90° ∴DE∥AC， ∴DE是△ABC的中位线， ∴E是AB的中点， ∴BE=AE， 课堂练习 A B C D E F ∴AE=CE， ∵∠BAC=60°， ∴△ACE是等边三角形， ∴CE=AC； ∵AF=CE， ∴AF=AE， ∵DF∥AC， ∴∠FEA=∠BAC=60°， ∴△AEF是等边三角形， ∴AF=EF， ∴AC=CE=EF=AF， ∴四边形ACEF是菱形。 课堂练习 A B C D O 3、如图，在菱形ABCD中，对角线AC与BC相交 于点O，图中有多少个等腰三角形和直角三角形？ 根据菱形的性质：四条边相等； 等腰三角形有：△ABD，△CBD， △ABC，△ADC。 根据菱形的性质：对角线互相平分； 直角三角形有：△ABO，△CBO， △ADO，△CDO。 课堂练习 A B C D E C’ 4、如图，在四边形纸片ABCD中，AD∥BC， AD>CD，将纸片沿过点D的直线折叠，使点C落在AD 上的点C’处，折痕DE交BC于点E，连接C’E。你能确 定四边形CDC’E的形状吗？证明你的结论。 四边形CDC’E是菱形 课堂练习 A B C D E C’ 证明：∵AD∥BC， ∴∠DC’E=∠C’EB， ∵折叠， ∴△DC’E≌△DCE， ∴∠DC’E=∠DCE ∴ ∠C’EB= ∠DCE， ∴C’E∥DC， ∴四边形CDC’E是平行四边形， ∵折叠， ∴ C’E=EC， ∴四边形CDC’E是菱形。 作业布置 课本第11页 习题6.3第1、2、3、4、5题 板书设计 菱形的面积= 对角线的乘积 1 2 菱形的面积 面积=底×高