八年级数学上册第一章勾股定理1探索勾股定理第2课时验证勾股定理及简单应用作业课件新版北师大版 21页

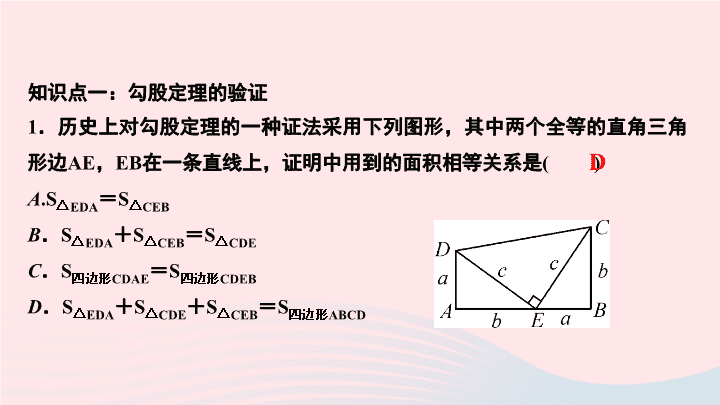
第一章　勾股定理 1．1　探索勾股定理 第2课时　验证勾股定理及简单应用 知识点一：勾股定理的验证 1 ．历史上对勾股定理的一种证法采用下列图形，其中两个全等的直角三角形边 AE ， EB 在一条直线上，证明中用到的面积相等关系是 ( ) A .S △EDA ＝ S △CEB B ． S △EDA ＋ S △CEB ＝ S △CDE C ． S 四边形 CDAE ＝ S 四边形 CDEB D ． S △EDA ＋ S △CDE ＋ S △CEB ＝ S 四边形 ABCD D 2 ．用四个边长均为 a ， b ， c 的直角三角板，拼成如图所示的图形．则下列结论中正确的是 ( ) A .c 2 ＝ a 2 ＋ b 2 B ． c 2 ＝ a 2 ＋ 2ab ＋ b 2 C ． c 2 ＝ a 2 － 2ab ＋ b 2 D ． c 2 ＝ (a ＋ b) 2 A 3 ．勾股定理的验证方法很多，用面积 ( 拼图 ) 证明是最常见的一种方法．如图所示，一个直立的长方体在桌面上慢慢地倒下，启发人们想到勾股定理的证明方法，设 AB ＝ c ， BC ＝ a ， AC ＝ b ，请你结合图形证明勾股定理． 知识点二：应用勾股定理解决实际问题 4 ．为了迎接新年的到来，同学们做了许多拉花布置教室，准备召开新年晚会，小王搬来一架长为 2.5 米的木梯，准备把梯子架到 2.4 米高的墙上，则梯脚与墙角的距离为 ( ) A ． 0.7 米 B ． 0.8 米 C ． 0.9 米 D ． 1.0 米 A 5 ．放学后，贝贝和京京从学校分手，分别沿西南方向和东南方向回家，已知两人行走的速度都是 40 m / min . 贝贝用 15 min 到家，京京用 20 min 到家，那么贝贝家与京京家的距离是 ( ) A ． 600 m B ． 800 m C ． 1000 m D ．无法计算 C 6 ．如图，在长方形 ABCD 中， AB ＝ 2 ， BC ＝ 4 ，对角线 AC 的垂直平分线分别交 AD ， AC 于点 E ， O ，连接 CE ，则 CE 的长为 ( ) A ． 3 B ． 3.5 C ． 2.5 D ． 2.8 C 7 ．如图，某人从点 A 出发，想垂直横渡到河对岸的 B 点，由于水流的影响，他实际上岸的地点 C 偏离了想要到达的 B 点 140 米 ( 即 BC ＝ 140 米 ) ，其结果是他在水中实际游了 500 米 ( 即 AC ＝ 500 米 ) ，则该河流 AB 处的宽度是 ______ 米． 480 8 ．如图，为修通铁路需凿通隧道 AC ，测得∠ C ＝ 90° ， AB ＝ 5 km ， BC ＝ 4 km ，若每天开凿隧道 0.3 km ，试计算需要几天才能把隧道 AC 凿通？ 解：在 Rt △ABC 中， AC 2 ＝ AB 2 － BC 2 ＝ 9 ，即 AC ＝ 3 km ， 3÷0.3 ＝ 10( 天 ) ，即需要 10 天才能把隧道 AC 凿通 9 ．一个圆柱形笔筒底面半径为 5 cm ，高 24 cm ，则笔筒内所能容下最长的笔为 ( ) A ． 20 cm B ． 24 cm C ． 26 cm D ． 30 cm C 10 ． ( 泸州中考 ) “ 赵爽弦图 ” 巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的 “ 赵爽弦图 ” 是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为 a ，较短直角边长为 b. 若 ab ＝ 8 ，大正方形的面积为 25 ，则小正方形的边长为 ( ) A ． 9 B ． 6 C ． 4 D ． 3 D 11 ．一辆装满货物，宽为 2.4 m 的卡车，欲通过如图所示的隧道，则卡车的高必须低于 ( ) A ． 4.1 m B ． 4.0 m C ． 3.9 m D ． 3.8 m A 13 ． ( 长春中考 ) 如图①，这个图案是我国汉代的赵爽在注解 《 周髀算经 》 时给出的，人们称它为 “ 赵爽弦图 ” ．此图案的示意图如图②，其中四边形 ABCD 和四边形 EFGH 都是正方形，△ ABF ，△ BCG ，△ CDH ，△ DAE 是四个全等的直角三角形．若 EF ＝ 2 ， DE ＝ 8 ，则 AB 的长为 _____ ． 10 14 ．如图①所示，一个梯子 AB 长 2.5 米，顶端 A 靠在墙 AC 上，这时梯子下端 B 与墙角 C 距离为 1.5 米，梯子滑动后停在 DE 的位置上，如图②，测得 BD 长为 0.5 米，则梯子顶端 A 下滑了多少米？ 解：在 Rt △ABC 中， AC 2 ＝ AB 2 － BC 2 ＝ 4 ，即 AC ＝ 2 米．在 Rt △CDE 中， CE 2 ＝ DE 2 － CD 2 ＝ 2.25 ，即 CE ＝ 1.5 米，所以 AE ＝ 2 － 1.5 ＝ 0.5( 米 ) ，即梯子顶端 A 下滑了 0.5 米 15 ．如图， AB 为一棵大树，在树上距地面 10 m 的 D 处有两只猴子，它们同时发现 C 处有一筐水果，一只猴子从 D 处往上爬到树顶 A 处，又沿滑绳 AC 到达 C 处，另一只猴子从 D 处滑到 B 处，再由 B 处跑到 C 处．已知两只猴子所经过的路程都为 15 m ，求树高 AB. 解：设 AD ＝ x m ，则 AB ＝ x ＋ 10 ， AC ＝ 15 － x ，在 Rt △ABC 中，根据勾股定理，得 (x ＋ 10) 2 ＋ (15 － 10) 2 ＝ (15 － x) 2 ，解得 x ＝ 2 ，所以 AB ＝ 12 m ．答：树高 AB 为 12 m 16 ．学习了勾股定理以后，有同学提出 “ 在直角三角形中，三边满足 a 2 ＋ b 2 ＝ c 2 ，或许其他的三角形三边也有类似的关系 ” ，让我们来做一个试验！ (1) 已知△ ABC 较短的两条边长分别是 a ＝ 6 mm ， b ＝ 8 mm ； ①△ ABC 是锐角三角形，最长的一条边长 c ＝ 9 mm ，则 a 2 ＋ b 2______ c 2 ( 填写“ >”“<” 或 “ ＝ ” ) ； ②△ ABC 是钝角三角形，最长的一条边长 c ＝ 11 mm ，则 a 2 ＋ b 2______ c 2 ( 填写“ >”“<” 或 “ ＝ ” ) ； (2) 根据以上的操作和结果，对这位同学提出的问题，你猜想的结论是：若△ ABC 是锐角三角形，最长的边长为 c ，则有 ___________ ；若△ ABC 是钝角三角形，∠ B 为钝角，则有 ___________ ．类比勾股定理的验证方法，说明其成立的理由． > < a 2 ＋ b 2 >c 2 a 2 ＋ c 2 0 ， x>0 ，所以 2ax>0 ，所以 a 2 ＋ b 2 >c 2 ；当△ ABC 为钝角三角形时证法类似，证法略