八年级上数学课件八年级上册数学课件《全等三角形的判定》 人教新课标 (7)_人教新课标 16页

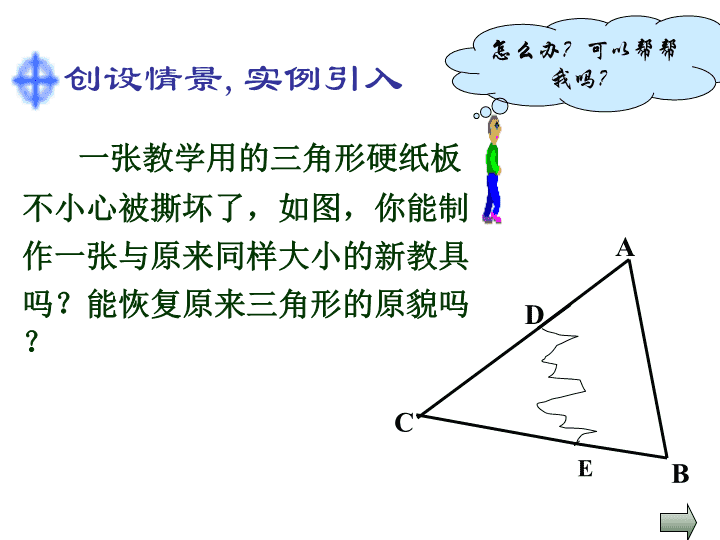
12.2全等三角形的条件 （ASA）（AAS） 1.什么是全等三角形？ 2. 我们已学了那些判定三角形全等的方法? 复习 三边对应相等的两个三角形全等。 边边边（SSS）： 边角边（SAS）： 有两边和它们夹角对应相等的两个 三角形全等。 一张教学用的三角形硬纸板 不小心被撕坏了，如图，你能制 作一张与原来同样大小的新教具 吗？能恢复原来三角形的原貌吗？ 怎么办？可以帮帮 我吗？创设情景,实例引入 C BE A D 探究1 如果两个三角形具备两角一边对应相等， 有几种可能情况？ 1、两角夹边对应相等。 共三种情况 2、有两个角和其中一个角的对边对应相等 3、有两个角对应相等，以及一个三角形中的夹 边与另一个三角形中一对应角的对边对应相等。 我们先来探究两角夹边对应相等时 两个三角形是否全等 先任意画一个△ABC，再画一个△DEF 使得EF=BC， ∠E = ∠B ，∠F = ∠C； 画法： 1、画EF=BC 2、画∠MEF = ∠B;再画∠NFE= ∠C EM、FN交于点D. D E F A B C A B C A B C A B C MN 观察所得的两个三角形是否全等。 公理3（全等三角形判定3） 有两个角和它们夹边对应相等的两个 三角形全等 用符号语言表达为： A B C D E F 在△ABC与△DEF中 ∴ △ABC≌ △DEF（ASA） ∠A= ∠D ∠B = ∠E AB=DE (简写成“角边角”或“ASA”）。 如图： 在△ABC和△DEF中，∠A=∠D， ∠B=∠E ，BC=EF，△ABC与△DEF全等吗？ 能利用角边角条件证明你的结论吗？ 探究2 A B C D E F 证明：∵ ∠A＋∠B＋∠C=180o ∠D＋∠E＋∠F=180o ∴ ∠C=∠F 又∵ ∠A=∠D， ∠B=∠E 在△ABC和△DEF中 ∠B=∠E ∠C=∠F BC=EF ∴ △ABC≌ △DEF （ASA） 有两个角和其中一个角的对边对应相等 的两个三角形是否全等？ 有两个角和其中一个角的对边对应相等 的两个三角形全等。 公理3的推论 A B C D E F 用符号语言表达为： 在△ABC和△DEF中 ∴ △ABC≌ △DEF （AAS） ∠A= ∠D BC=EF ∠B = ∠E (简写成“角角边”或“AAS”） 例题讲解： 例1.已知：点D在AB上，点E在AC上，BE和CD 相交于点O，AB=AC，∠B=∠C。 求证：BD=CE A ED CB O 如果把已知中的AB=AC改成 AD=AE, 那么BD和 CE还相等么？为什么？ 思考 探究3 有两个角对应相等，以及一个三角形中两 个对应角的夹边与另一个三角形中一对应角 的对边对应相等的两个三角形是否全等呢？ A B C D 观 察 如图：△ABC是直角三角形， ∠ACB＝90o , AB,垂足为D。 则在△ACD与△CBD中便有： ∠A= ∠1 ∠ADC= ∠CDB=90o CD=CD 试想△ACD与△CBD会全等吗？ （ 1 两个三角形并非有两角一边对应相等便能判别它 们全等，只有满足（ASA）和（AAS）才行。 例2.如图，∠1=∠2，∠3=∠4 求证：AC=AD 如果把已知中的 ∠3=∠4 改成, ∠D=∠C 此题又如何? C A D 1 B2 3 4 O A C D B AO=BO 1.如图，AB、CD相交于点O，已知∠A=∠B 添加条件 （填一个即可） 就有 △AOC≌ △BOD 还有吗？ 填一填 1、如图，已知∠1=∠2，∠3=∠4，BD=CE 求证：AB=AC 4 21 3 A B CED 2、如图，AB∥CD，AD∥BC，那么AB=CD吗？ 为什么？AD与BC呢？ A B CD 1 2 3 4 1.如图，要测量河两岸相对的两点A，B的距离， 可以在AB的垂线BF上取两点C，D，使BC=CD， 再定出BF的垂线DE，使A， C，E在一条直线上， 这时测得DE的长就是AB的长。为什么？ A B C D E F 2、如图，已知∠1=∠2 ∠3=∠4 求证：BD=CD A B CD E 1 2 3 4 1. 已知:点E是正方形ABCD的边CD上一点， 点F是CB的延长线上一点，且EA⊥AF， 求证：DE=BF A B C D E F 2. 如图，CD⊥AB于D， BE⊥AC与E，BE、CD 交于O，且AO平分 ∠BAC，求证：OB=OC A B C ED O 1.你能总结出我们学过哪些判定三角形 全等的方法吗？ 2.要根据题意选择适当的方法。 3.证明线段或角相等，就是证明它们所 在的两个三角形全等。