八年级上数学课件- 11-2-1 三角形的内角 课件（共15张PPT）_人教新课标 15页

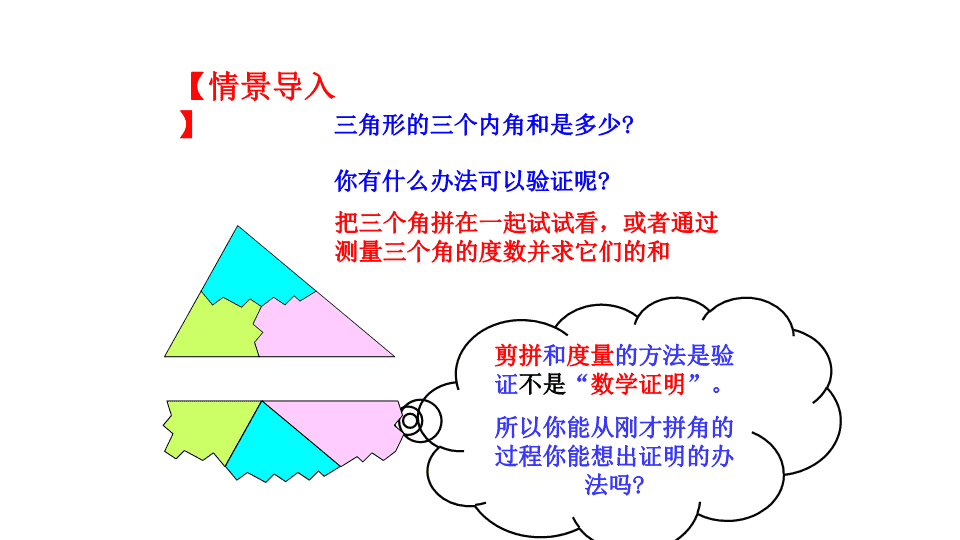
11.2 与三角形有关的角 11.2.1 三角形的内角 三角形的三个内角和是多少? 把三个角拼在一起试试看，或者通过 测量三个角的度数并求它们的和 你有什么办法可以验证呢? 剪拼和度量的方法是验 证不是“数学证明”。 所以你能从刚才拼角的 过程你能想出证明的办 法吗? 【情景导入】 CB A 猜想：三角形三个内角的和等于180° 已知△ＡＢＣ，求证：∠A+∠B+∠C=180° 【合作探究】 证法１：过A作EF∥BC， ∴∠B=∠2, (两直线平行,内错角相等) ∠C=∠1. (两直线平行,内错角相等) 又∵∠2+∠1+∠BAC=180°, ∴∠B+∠C+∠BAC=180°. F 2 1 E CB A 三角形内角和定理：三角形三个内角的和等于180° 证法２：延长BC到D，过C作CE∥BA， ∴ ∠A=∠1,(两直线平行，内错角相 等) ∠B=∠2.(两直线平行，同位角相等) 又∵∠1+∠2+∠ACB=180°, ∴∠A+∠B+∠ACB=180°. 21 E DCB A 三角形内角和定理：三角形三个内角的和等于180° 证法3：过A作AE∥BC， ∴∠B=∠BAE, (两直线平行,内错角相等) ∠EAB+∠BAC+∠C=180°, (两直线平行,同旁内角互补) ∴∠B+∠C+∠BAC=180°. CB E A 三角形内角和定理：三角形三个内角的和等于180° 在这里，为了证明的需要，在原来的图形上 添加的线叫做辅助线.在平面几何里，辅助线通 常画成虚线. 为了证明三个角的和为180°,转化为一个平 角或同旁内角互补,这种转化思想是数学中的常 用方法. 【归纳】 【例1】在△ABC中， ∠BAC=40°,∠B=75° , AD是△ABC的角平分线,求∠ADB的度数？ 【典例1】 ∵ ∠B= 75° 解：∵ ∠ BAC=40 °， AD是△ABC角平分线 ∴ ∠ADB＝180 ° ﹣ ∠B﹣∠BAD = 180 ° - 75°- 20° A C B Ｄ 202 1  ABEDAB （1）在△ABC中，∠A=55°， ∠ B=43°,则∠ACB= ， ∠ACD＝______. （2）在△ABC中,∠A=80°, ∠B=∠C , 则∠C＝____°. 82° CB A Ｄ 98° 50 【跟踪训练】 如图,C岛在A岛的北偏东50°方向，B 岛在A岛的北偏东80°方向，C岛在B岛 的北偏西40°方向。求下面各题. （1）∠DAC＝_____ ∠DAB＝______ ∠EBC＝_______ ∠CAB ＝ ______ A(2)从C岛看A 、B两岛的视角∠C是多少? 50° 80° 40° D B C E北 北 解：∵ AD∥BE ∴ ∠DAB﹢∠ABE＝180° ∴ ∠ABE ＝ 180°－∠DAB ＝ 180° － 80° ＝100° 在△ABC中,∠C ＝ 180° － ∠CAB － ∠ABC ＝ 180°－30 °－60 °＝90° ∴ ∠ABC＝∠ABE﹣∠CBE 30 ° ＝100°﹣40°＝60° P12例1 解法一【典例2】 B D C E北 A 你能想出一个更 简捷的方法来求 ∠C的度数吗？1 2 50° 40° 解： 过点C画CF∥AD ∴ ∠1＝∠DAC＝50 °, F ∵ CF∥AD, 又AD ∥BE ∴ CF∥ BE ∴∠2＝∠CBE ＝40 ° ∴ ∠ACB＝∠1﹢∠2 ＝50 °﹢ 40 ° ＝90 ° P12例1 解法二 1.如图，∠A+∠B+∠C+∠D+∠E+∠F= . A B C D E F 【解析】 ∠A，∠C，∠E是△ACE的三个内角， 其和为180°， ∠B，∠D，∠F是△BDF的三个内 角，其和为180°，所以六个角的和为 360°. 【答案】360° 【跟踪训练】 2、教科书13页练习的第1题 三角形的内 角和等于 180°. 证法 应用 转化为一个平 角或同旁内角 互补 求角度 作平行线 转化思想 辅助线通过本课时的学习，需要我们掌握： 数学练习册11.2.1 作业布置：