八年级数学下册知能提升作业二十九第20章平行四边形的判定20 4页

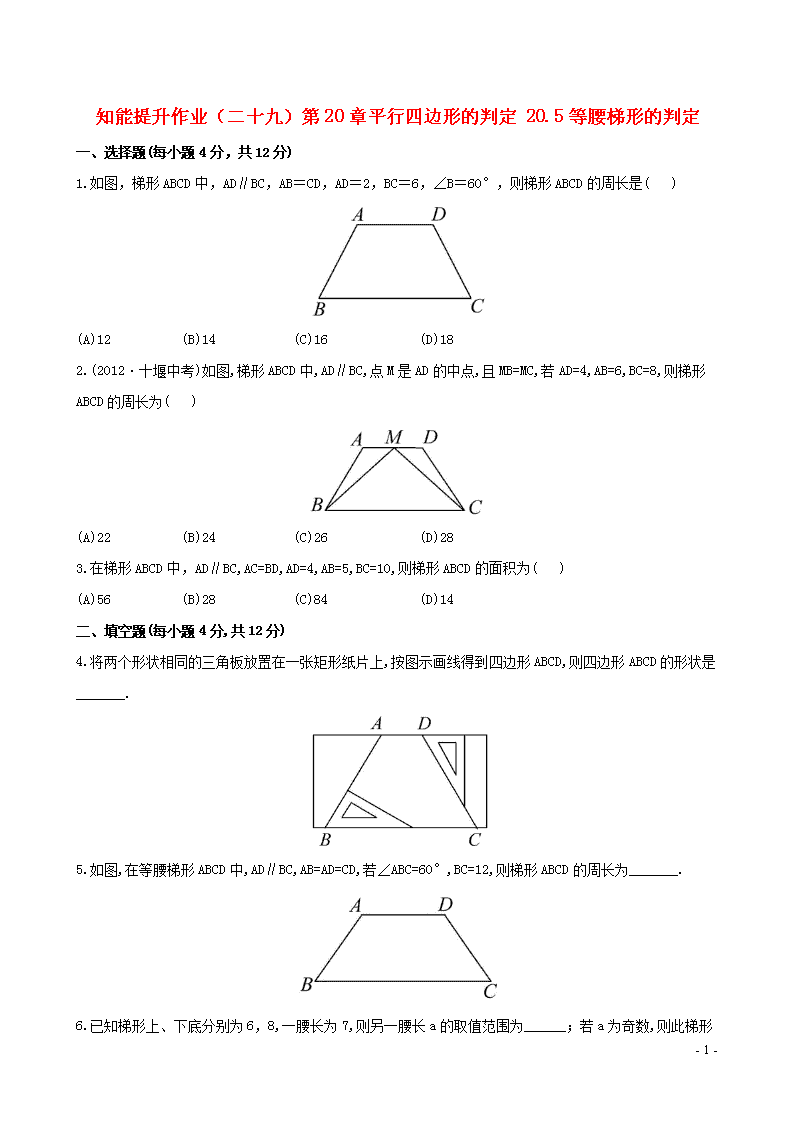
- 1 - 知能提升作业（二十九）第 20 章平行四边形的判定 20.5 等腰梯形的判定 一、选择题(每小题 4 分，共 12 分) 1.如图，梯形 ABCD 中，AD∥BC，AB＝CD，AD＝2，BC＝6，∠B＝60°，则梯形 ABCD 的周长是( ) (A)12 (B)14 (C)16 (D)18 2.(2012·十堰中考)如图,梯形 ABCD 中,AD∥BC,点M 是 AD 的中点,且 MB=MC,若 AD=4,AB=6,BC=8,则梯形 ABCD 的周长为( ) (A)22 (B)24 (C)26 (D)28 3.在梯形 ABCD 中，AD∥BC,AC=BD,AD=4,AB=5,BC=10,则梯形 ABCD 的面积为( ) (A)56 (B)28 (C)84 (D)14 二、填空题(每小题 4 分,共 12 分) 4.将两个形状相同的三角板放置在一张矩形纸片上,按图示画线得到四边形 ABCD,则四边形 ABCD 的形状是 _______. 5.如图,在等腰梯形 ABCD 中,AD∥BC,AB=AD=CD,若∠ABC=60°,BC=12,则梯形 ABCD 的周长为_______. 6.已知梯形上、下底分别为 6，8,一腰长为 7,则另一腰长 a 的取值范围为______；若 a 为奇数,则此梯形 - 2 - 为_________梯形. 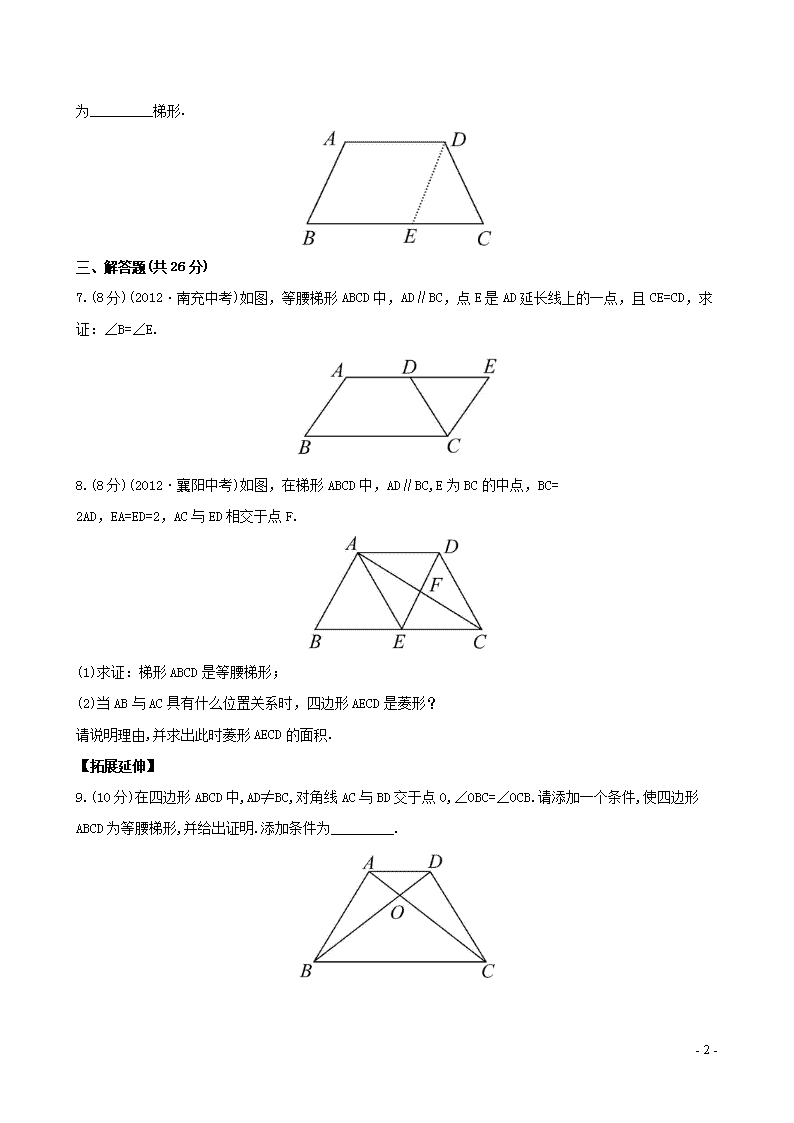三、解答题(共 26 分) 7.(8 分)(2012·南充中考)如图，等腰梯形 ABCD 中，AD∥BC，点 E 是 AD 延长线上的一点，且 CE=CD，求 证：∠B=∠E. 8.(8 分)(2012·襄阳中考)如图，在梯形 ABCD 中，AD∥BC,E 为 BC 的中点，BC= 2AD，EA=ED=2，AC 与 ED 相交于点 F. (1)求证：梯形 ABCD 是等腰梯形； (2)当 AB 与 AC 具有什么位置关系时，四边形 AECD 是菱形？ 请说明理由,并求出此时菱形 AECD 的面积. 【拓展延伸】 9.(10 分)在四边形 ABCD 中,AD≠BC,对角线 AC 与 BD 交于点 O,∠OBC=∠OCB.请添加一个条件,使四边形 ABCD 为等腰梯形,并给出证明.添加条件为_________. - 3 - 答案解析 1.【解析】选 C.作 AE⊥BC,DF⊥BC,垂足分别为 E,F. ∵AD∥BC,AD=2，BC=6，∠B=60°，∴AB=4， ∴梯形周长为：4+2+4+6=16.故 C 正确. 2.【解析】选 B.∵MB=MC,∴∠MBC=∠MCB,∵AD∥BC,∴∠AMB=∠MBC,∠DMC=∠MCB,∴∠AMB=∠DMC,又∵M 是 AD 的中点,∴AM=DM,∴△AMB≌△DMC,∴AB=DC,因此周长为 AB+BC+CD+AD=2AB+BC+AD=24. 3.【解析】选 B.如图，∵AC=BD, ∴梯形 ABCD 为等腰梯形， 过点 A 作 AE⊥BC 于 E，则 10 4BE 3,2   又 AB=5，∴AE=4,  ABCD 1S 4 10 4 28.2     梯形 4.【解析】因为 AD∥BC,显然四边形 ABCD 是梯形,又∠ABC=∠DCB=60°,根据“在同一底上的两个角相等的 梯形是等腰梯形”,所以四边形 ABCD 是等腰梯形. 答案：等腰梯形 5.【解析】连结 BD,如图. ∵AB=AD,∴∠ABD=∠ADB.又 AD∥BC, ∴∠DBC=∠ADB,即∠ABD=∠DBC.由 ∠ABC=60°,得∠DBC=30°.根据等腰梯形的性质,∠C=∠ABC=60°, ∴∠BDC=180°-30°-60°=90°.即△BDC 为直角三角形, ∴DC=AD=AB= 1 2 BC=6.∴梯形 ABCD 的周长为 12+3×6=30. 答案：30 6.【解析】作 DE∥AB,则四边形 ABED 为平行四边形,即 BE=AD,所以, EC=8-6=2,DE=AB=7.由三角形的三边关系可知,DC 的取值范围为 7-2＜a＜7+2, 即 5＜a＜9.当 a 取奇数时, 即 a=7 时,AB=DC,所以梯形 ABCD 为等腰梯形. 答案：5＜a＜9 等腰 7.【证明】∵四边形 ABCD 为等腰梯形，AD∥BC， ∴∠B=∠BCD,∠BCD=∠CDE,∴∠B=∠CDE, - 4 - 又∵CD=CE,∴∠CDE=∠E,∴∠B=∠E. 8.【解析】(1)∵AD∥BC, ∴∠DEC=∠EDA,∠BEA=∠EAD. 又∵EA=ED,∴∠EAD=∠EDA. ∴∠DEC=∠AEB. 又∵EB=EC,∴△DEC≌△AEB. ∴AB=DC,又∵AD∥BC, ∴梯形 ABCD 是等腰梯形. (2)当 AB⊥AC 时，四边形 AECD 是菱形. 证明如下： ∵AD∥BC,BE=EC=AD, ∴四边形 AECD 为平行四边形， ∵AB⊥AC,∴AE=BE=EC， ∴四边形 AECD 是菱形. 过 A 作 AG⊥BE 于点 G,∵AE=BE=AB=2, ∴△ABE 是等边三角形,∴∠AEB=60°, AG 3,  AECDS EC AG 2 3 2 3.    菱形 9.【解析】添加条件为 AD∥BC. ∵AD∥BC,AD≠BC, ∴AB 和 CD 不平行, ∴四边形 ABCD 是梯形. ∵AD∥BC,∠OBC=∠OCB. ∴∠DAO=∠ADO,OB=OC. ∴OA=OD. ∴AC=BD ∵BC=BC, ∴△ABC≌△DCB. ∴AB=DC. ∴四边形 ABCD 是等腰梯形.