八年级数学下册知能提升作业十七第19章全等三角形19 4页

知能提升作业（十七）‎ 第19章 全等三角形19.2全等三角形的判定1-2全等三角形的判定条件边角边 ‎ 一、选择题(每小题4分，共12分)‎ ‎1.全等三角形是( )‎ ‎(A)三个角对应相等的三角形 ‎(B)周长相等的两个三角形 ‎(C)面积相等的两个三角形 ‎(D)三边对应相等和三个角对应相等的两个三角形 ‎2.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )‎ ‎(A)20° (B)30° (C)35° (D)40°‎ ‎3.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )‎ ‎(A)甲和乙 (B)乙和丙 ‎(C)只有乙 (D)只有丙 二、填空题(每小题4分,共12分)‎ ‎4.如图，点B在∠CAD的平分线上，请添加一个适当的条件:_____________,使△ABC≌△ABD(只填一个即可).‎ - 4 -‎ ‎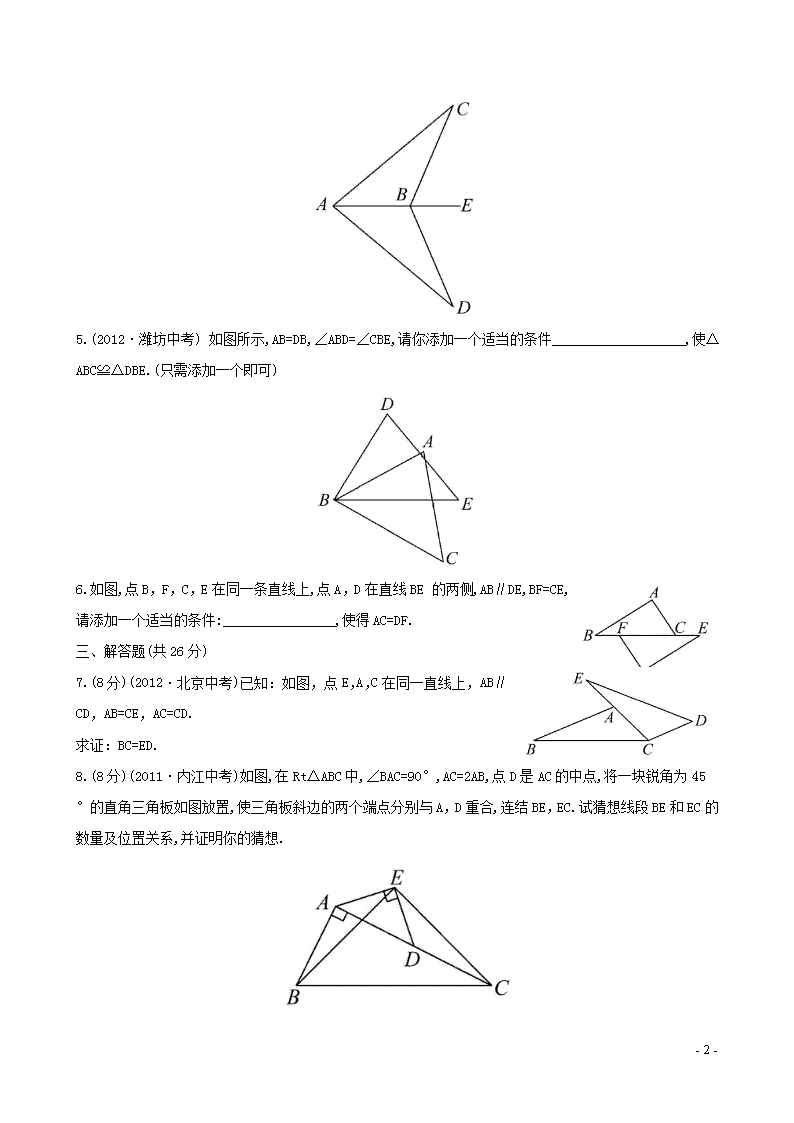5.(2012·潍坊中考) 如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件___________________,使△ABC≌△DBE.(只需添加一个即可)‎ ‎6.如图,点B，F，C，E在同一条直线上,点A，D在直线BE 的两侧,AB∥DE,BF=CE,请添加一个适当的条件:________________,使得AC=DF.‎ 三、解答题(共26分)‎ ‎7.(8分)(2012·北京中考)已知：如图，点E，A，C在同一直线上，AB∥CD，AB=CE，AC=CD.‎ 求证：BC=ED.‎ ‎8.(8分)(2011·内江中考)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A，D重合,连结BE，EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.‎ - 4 -‎ ‎【拓展延伸】‎ ‎9.(10分)学习“全等三角形”的知识时,老师布置了一道作业题:“如图1,已 知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使 ‎∠QAP=∠BAC,连结BQ,CP,则BQ=CP.”‎ 小亮是个爱动脑筋的同学,他通过对图1的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,将点P移到三角形ABC之外,原题中的条件不变,发现“BQ=CP”仍然成立,请你就图2给出证明.‎ 答案解析 ‎1.【解析】选D.根据全等三角形的定义,选项D正确.‎ ‎2.【解析】选B.因为△ACB≌△A′CB′,所以∠ACB=∠A′CB′,即∠ACA′=‎ ‎∠ACB-∠A′CB=∠A′CB′-∠A′CB=∠BCB′=30°.‎ ‎3.【解析】选C.依据“S.A.S.”只有三角形乙能和已知的三角形全等.‎ ‎4.【解析】由已知可知∠CAB=∠DAB,AB=AB,故若添加AC=AD，可利用S.A.S.证两三角形全等.‎ 答案：AC=AD ‎5.【解析】∵∠ABD=∠CBE,AB=BD,∴∠DBE=∠ABC,∴△ABC与△DBE满足一边与一角对应相等，添加的条件可满足夹角的另一边也对应相等，由S.A.S.证明两三角形全等.‎ 答案：BC=BE(答案不唯一)‎ ‎6.【解析】要使AC=DF,则必须满足△ABC≌△DEF,由已知AB∥DE,BF=CE,则可得到∠B=∠E,BC=EF,考虑S.A.S. 判定△ABC≌△DEF，添加AB=DE即可.‎ 答案：AB=DE ‎7.【证明】∵AB∥CD,‎ ‎∴∠BAC=∠ECD,‎ - 4 -‎ ‎∵AB=CE,AC=CD,‎ ‎∴△ABC≌△CED(S.A.S.)‎ ‎∴BC=ED.‎ ‎8.【解析】BE=EC,BE⊥EC.‎ 证明:∵AC=2AB,点D是AC的中点,‎ ‎∴AB=AD=CD.‎ ‎∵∠EAD=∠EDA=45°,‎ ‎∴∠EAB=∠EDC=135°.‎ ‎∵△AED是等腰直角三角形，‎ ‎∴EA=ED.‎ 在△EAB和△EDC中,‎ AB=DC ‎∠EAB=∠EDC EA=ED ‎ ‎∴△EAB≌△EDC(S.A.S.)‎ ‎∴∠AEB=∠DEC,EB=EC.‎ ‎∴∠BEC=∠AED=90°,‎ ‎∴BE=EC,BE⊥EC.‎ ‎9.【证明】∵∠QAP=∠BAC,‎ ‎∴∠QAP+∠PAB=∠BAC+∠PAB,‎ ‎∴∠QAB=∠PAC.‎ 在△ABQ和△ACP中,‎ AQ=AP ‎∠QAB=∠PAC AB=AC ‎ ‎∴△ABQ≌△ACP(S.A.S.),‎ ‎∴BQ=CP.‎ - 4 -‎