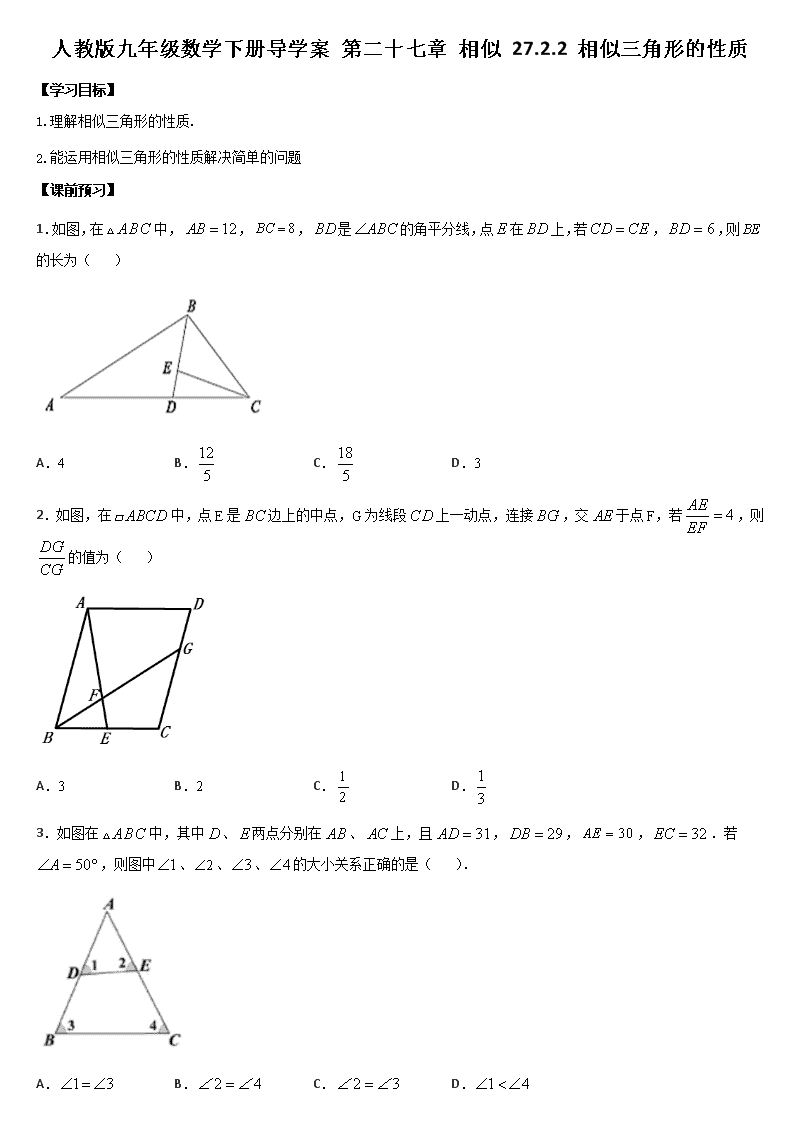人教版九年级数学下册导学案 第二十七章 相似 27相似三角形的性质 8页

人教版九年级数学下册导学案 第二十七章 相似 27.2.2 相似三角形的性质 【学习目标】 1.理解相似三角形的性质. 2.能运用相似三角形的性质解决简单的问题 【课前预习】 1．如图，在 ABC 中， 12AB  ， 8BC  ，BD 是 ABC 的角平分线，点 E 在 BD 上，若CD CE ， 6BD  ，则 BE 的长为（ ） A．4 B．12 5 C．18 5 D．3 2．如图，在 ABCD 中，点 E 是 BC 边上的中点，G 为线段 CD 上一动点，连接 BG ，交 AE 于点 F，若 4AE EF  ，则 DG CG 的值为（ ） A．3 B．2 C． 1 2 D． 1 3 3．如图在 ABC 中，其中 D 、E 两点分别在 AB 、AC 上，且 31AD  ， 29DB  ， 30AE  ， 32EC  ．若 50A   ， 则图中 1 、 2 、 3 、 4 的大小关系正确的是（ ）． A． 1 3   B． 2 4  C． 2 3  D． 1 4   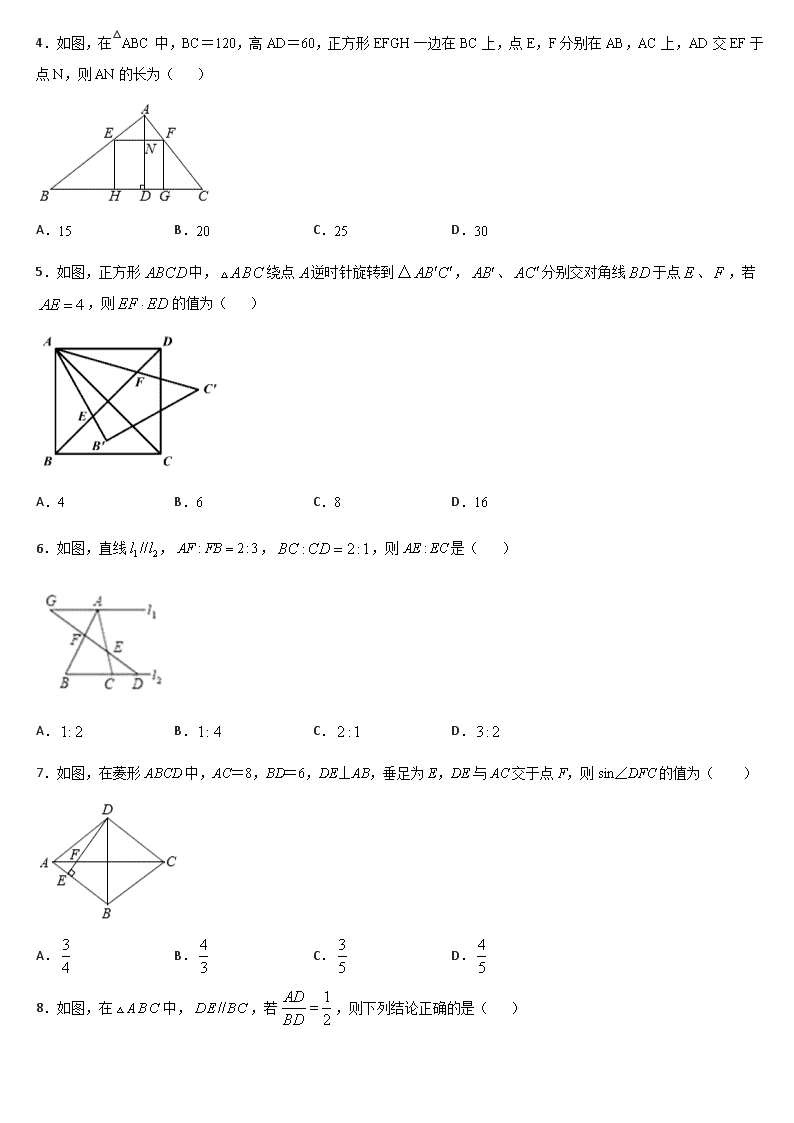4．如图，在△ABC 中，BC＝120，高 AD＝60，正方形 EFGH 一边在 BC 上，点 E，F 分别在 AB，AC 上，AD 交 EF 于点 N，则 AN 的长为（ ） A．15 B．20 C．25 D．30 5．如图，正方形 ABCD 中， ABC 绕点 A 逆时针旋转到 AB C △ ，AB、AC分别交对角线 BD 于点 E 、F ，若 4AE  ， 则 EF ED 的值为（ ） A．4 B．6 C．8 D．16 6．如图，直线 1 2//l l ， : 2 : 3AF FB  ， : 2:1BC CD  ，则 :AE EC 是（ ） A．1: 2 B．1: 4 C． 2:1 D．3:2 7．如图，在菱形 ABCD 中，AC＝8，BD＝6，DE⊥AB，垂足为 E，DE 与 AC 交于点 F，则 sin∠DFC 的值为（ ） A． 3 4 B． 4 3 C． 3 5 D． 4 5 8．如图，在 ABC 中， //DE BC ，若 1 2 AD BD  ，则下列结论正确的是（ ） A． 1 2 DE BC  B． 1 2 AG FG  C． ADE 周长： ABC 周长 1 2  D． ADE 面积： ABC 面积 1 3  9．如图，在正方形 ABCD 中，M 为 BC 上一点，连接 AM ，过 M 作 ME AM 交 CD 于点 F，交 AD 的延长线于点 E， 若 4, 2AB BM  ，则 DEF 的面积为（ ） A．3 B．4 C．8 D．9 10．如图，在 ABC 中，中线 BE ，CD 相交于点O ，连线 DE ，下列结论：① 1 2 DE BC  ；② 1 2 ADE ABC S S   ；③ AD OE AB OB  ； ④ 1 4 ODE DEC S S △ △ ．其中正确的是（ ） A．①②③ B．②③ C．④ D．①③ 【学习探究】 自主学习 阅读课本，完成下列问题 1．什么是相似三角形的相似比？ 2.已知： ∆ABC∽∆A’B’C’，根据相似的 定义，我们有哪些结论？（从对应边上看， 从对应角上看） 3.思考：两个三角形相似，除了对应边成比例、对应角相等之外，我们还可以得到哪些结论？ 4.如果两个三角形相似，它们的周长之间有什么关系？ 如果△ABC∽△A′B′C′，且△ABC 与△A′B′C′的相似比为 k，即 因此 AB= ， BC= ,CA= ， 从而 AB BC CA A B B C C A          =k 结论： . 同理，相似多边形的周长比等于 . 互学探究 探究一：相似三角形的性质 【小组讨论】如图，△ABC∽△A’B’C’相似比为 k，尝试解决下列问题： （1）它们对应高、对应中线、对应角平分线的比各是多少？ （2）相似形三角形面积的比与相似比有什么关系？ AB BC CA kA B B C C A         （3）你能归纳出相似三角形的性质吗？ 思考：相似形三角形的周长有什么关系？ 练习 如图，△ABC 中，D、E、F 分别是边 AB、BC、AC 的中点，若△ABC 的周长是 20cm，则△DEF 的周长是 （ ） A.5cm B.10cm C.15cm D.20cm 探究二：相似三角形性质的运用 如图，在△ABC 和△DEF 中，AB=2DE，AC=2DF，∠A=∠D。若△ABC 的边 BC 上的高为 6，面 积为 12 ，求 △DEF 的边 EF 上的高和面积。 【小组讨论】 （1）△ABC 和△DEF 相似吗？ （2）如何运用相似三角形的性质求△DEF 的边 EF 上的高和面积？ 练习 1.如图 1 已知 D、E 分别是△ABC 的 AB、 AC 边上的点，DE∥BC 且 S△ADE：S 四边形 DBCE=1:8，那么 AE:AC 等于（ ） A．1:9 B．1:3 C．1:8 D． 1:2 2.在△ABC 和△DEF 中，AB=2DE，AC=2DF，∠A=∠D，如果△ABC 的周长是 16，面积是 12，那么△ DEF 的周长、面积依次为（ ） A．8，3 B．8，6 C．4，3 D．４，6 3.如图 2 所示，□ABCD 中，AE:EB=1:2，S△AEF=6cm2，则 S△CDF= ． 【课后练习】 1．如图，在 △ ABC 中，中线 BE、CD 相交于点 O，连结 DE，下列结论中，正确的个数有（ ） ① 1 2 DE BC  ；② 1 2 DOE COB S S    ；③ AD OE AB OB  ；④ 1 3 COE ADC S S    ． 讨论： ①对应高的关系 ②对应中线的关系 ③对应角平分线的关系 ④对应周长的关系 ⑤对应面积的关系 归纳相似三角形性质： （几何命题可以用代数计算方法证明） 先证明两个三角形相似 ，求出相似比，然后利用性质， 由一个三角形的高和面积求得另一个三角形的高和面积。 (2) B A C D E 题（1） A．1 个 B．2 个 C．3 个 D．4 个 2．如图，正方形 ABCD 中，点 F 是 BC 边上一点，连接 AF ，以 AF 为对角线作正方形 AEFG ，边 FG 与正方形 ABCD 的对角线 AC 相交于点 H ，连接 DG ．以下四个结论： ① EAB GAD   ；② AFC AGDV V∽ ；③ 2AE AH AC  ；④ DG AC ． 其中正确的个数为（ ） A．1 个 B．2 个 C．3 个 D．4 个 3．如图，已知四边形 ABCD 是矩形，把矩形沿直线 AC 折叠，点 B 落在点 E 处，连接 DE ．若 : 3:5DE AC  ，则 AD AB 的值为（ ） A． 2 2 B． 2 3 C． 1 2 D． 3 3 4．如图， ABC 中， / / ,DE BC D E、 分别在 AB AC、 上，若 : 2: 3AD DB  ，则（ ） A． : 2:3DE BC  B． : 4:9ADE DECBS S V 四边形 C． : 3:5EC AC  D． : 3: 5AE AC  5．如图，在 Rt ABC 中， 90 ,ACB AC BC  o ，点 D、E 在 AB 边上， 45DCE   ，若 3, 4AD BE  ，则 ABC∣ 的面积为（ ） A．20 B．24 C．32 D．36 6．如图，在正方形 ABCD 中，E 是 BC 的中点，F 是 CD 上的一点，AE⊥EF，则下列结论正确的是（ ） A．∠BAE＝30° B．△ABE≌△AEF C．CE2＝AB•CF D．CF＝ 1 3 CD 7．若 △ ABC∽△DEF，它们的相似比为 4：1，则 △ ABC 与 △ DEF 的周长比为（ ） A．2：1 B．4：1 C．8：1 D．16：1 8．如图，在 ABCD 中， 7AB  ， 3BC  ， ABC 的平分线交CD 于点 F ，交的延长线于点 E ，若 2BF  ，则线 段 EF 的长为（ ） A．4 B．3 C． 8 3 D． 7 4 9．如图，在 △ ABC 中，AB＝AC=5，BC＝2 5 ，若点 O 为 △ ABC 三条高的交点，则 OA 的长度为（ ） A． 3 5 2 B． 2 5 3 C． 5 D． 3 5 4 10．如图，在正方形 ABCD 中，点 E 是边 BC 的中点，连接 AE ， EF AE 交 CD 边于点 F ，已知 4AB  ，则CF 的长为（ ） A．1 B． 5 5 C．3 D．2 第 II 卷（非选择题） 请点击修改第 II 卷的文字说明 二、填空题 11．如图，Rt△ABC 中，∠ACB＝90°，CD⊥AB 于 D． 若 AD＝3，BD＝2，则 BC=_______________． 12．如图， ABC 中，如果 AB AC ，AD BC 于点 D ，M 为 AC 中点，AD 与 BM 交于点G ，那么 :GDM GABS S△ △ 的值为______． 13．两个相似三角形的面积之差为 23cm ，周长比是 2：3，那么较小的三角形面积是______ 2cm ． 14．如图，矩形 ABCD 中，对角线 AC 、 BD 交于点O ， AE BD 于点 E ，若 6AB  ， 5OD  ，则 AE  ________． 15．在矩形 ABCD 中， ABC 的平分线交 AD 于点 E， BED 的平分线交 DC 于点 F，若 12AB  ，点 F 恰为 DC 的 三等分点，则 BC  ________（结果保留根号） 【参考答案】 【课前预习】 1．A 2．C 3．C 4．B 5．D 6．C 7．D 8．B 9．D 10．D 【课后练习】 1．C 2．C 3．C 4．C 5．D 6．C 7．B 8．C 9．A 10．A 11． 10 12．1: 4 13．12 5 14．4.8 15． 4 8 2 或8 4 2