2019九年级数学上册 第二十四章弧长和扇形面积 6页

弧长和扇形面积 课题： 24．4弧长和扇形面积（2）‎ 课时 ‎ 1 课 时 教学设计 课 标 要 求 会计算圆的弧长、扇形的面积 教 材 及 学 情 分 ‎ 析 ‎ 1、 教材分析：‎ ‎ 学生在学习本章之前，已通过折叠、对称、平移、旋转、推理证明等方式认识了许多图形的性质，积累了大量的空间与图形的经验．本章是在学习了这些直线型图形的有关性质的基础上，进一步来探索一种特殊的曲线──圆的有关性质．通过本章的学习，对学生今后继续学习数学，尤其是逐步树立分类讨论的数学思想、归纳的数学思想起着良好的铺垫作用．本章的学习是高中的数学学习，尤其是圆锥曲线的学习的基础性工程．‎ 学情分析：‎ ‎ 2、九年级学生已具备一定知识储备和认知能力。但学生的基础较差，中等、差等生较多，优等生较少。课堂上，多数学生表现欲不强，发言不积极，怕回答错问题；学生应用知识灵活解决问题的能力较差，在几何证明题中，不会抓住已知条件进行论证推理。因此，在教学中，注重学生学习方法的培养，通过学生实践、探究、合作交流来完成本节课的教学。‎ 课 时 教 学 目 标 ‎1．了解母线的概念．‎ ‎2．掌握圆锥的侧面积计算公式，并会应用公式解决问题．‎ ‎3．经历探索圆锥侧面积计算公式的过程，发展学生的实践探索能力．‎ 重点 ‎1．经历探索圆锥侧面积计算公式的过程．2．了解圆锥的侧面积计算公式，并会应用公式解决问题．‎ 难点 ‎ 圆锥侧面积计算公式的推导过程 6‎ 提炼课题 ‎ 圆锥侧面积公的推导及其应用 教法学法 指导 ‎ 合作探究法 引导启发法 练习法 教具 准备 ‎ 课件 教学过程提要 环节 学生要解决的问 题或完成的任务 师生活动 设计意图 引 入 新 课 一、复习：‎ ‎ ‎ 二、由生活中的圆锥形象导入新课 一、复习：‎ ‎1、弧长怎么计算?说一说弧长的计算公式。‎ ‎2、扇形的面积怎么计算？说一说扇形面积的计算公式？‎ ‎ 3、弧长公式和扇形面积公式有什么区别？‎ 二、导入新课 师：大家见过圆锥吗？你能举出实例吗？‎ 生：见过，如漏斗、蒙古包．‎ 师：你们知道圆锥的表面是由哪些面构成的吗？请大家互相交流．‎ 巩固上节课所学的知识，为本节课做铺垫。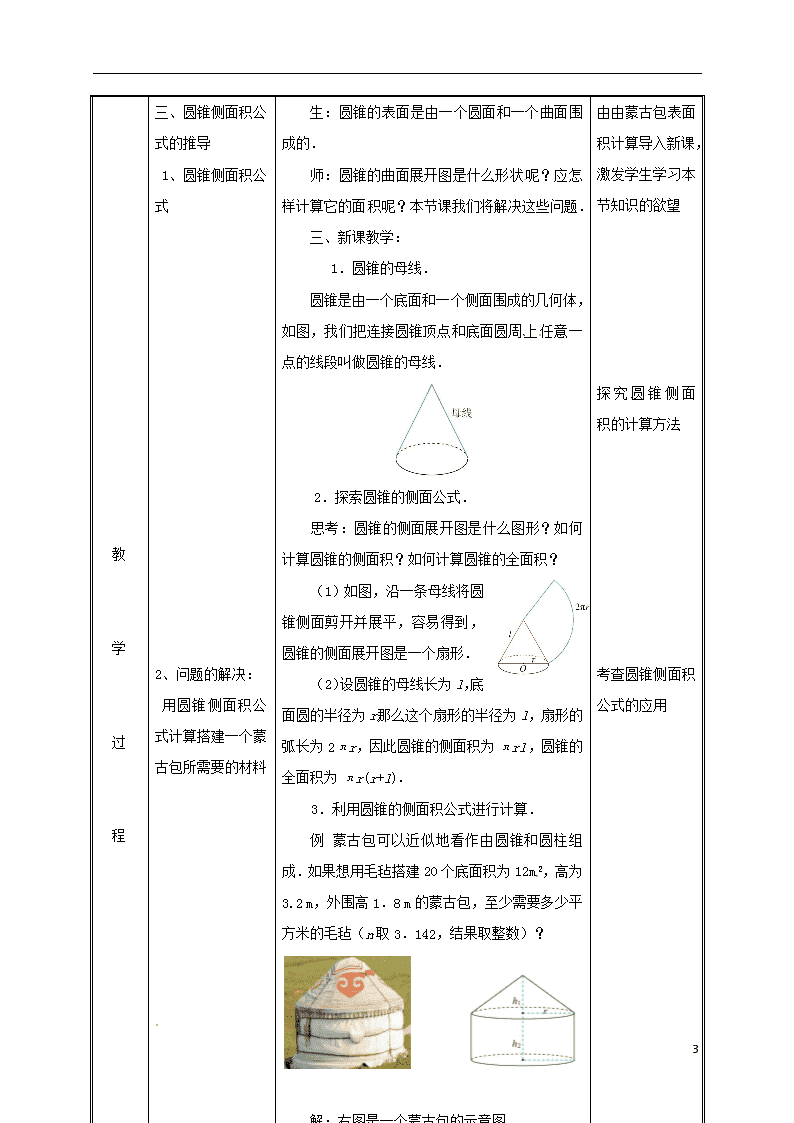‎ 6‎ 教 学 过 程 三、 圆锥侧面积公式的推导 ‎ 1、圆锥侧面积公式 ‎2、问题的解决：‎ ‎ 用圆锥侧面积公式计算搭建一个蒙古包所需要的材料 生：圆锥的表面是由一个圆面和一个曲面围成的．‎ 师：圆锥的曲面展开图是什么形状呢？应怎样计算它的面积呢？本节课我们将解决这些问题．‎ 三、 新课教学：‎ ‎ 1．圆锥的母线．‎ 圆锥是由一个底面和一个侧面围成的几何体，如图，我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线．‎ ‎2．探索圆锥的侧面公式．‎ 思考：圆锥的侧面展开图是什么图形？如何计算圆锥的侧面积？如何计算圆锥的全面积？‎ ‎（1）如图，沿一条母线将圆锥侧面剪开并展平，容易得到，圆锥的侧面展开图是一个扇形．‎ ‎（2）设圆锥的母线长为l，底面圆的半径为r，那么这个扇形的半径为l，扇形的弧长为2πr，因此圆锥的侧面积为πrl，圆锥的全面积为πr(r+l)．‎ ‎3．利用圆锥的侧面积公式进行计算．‎ 例 蒙古包可以近似地看作由圆锥和圆柱组成．如果想用毛毡搭建20个底面积为‎12 m2，高为‎3.2 m，外围高1．‎8 m的蒙古包，至少需要多少平方米的毛毡（n取3．142，结果取整数）？‎ ‎ ‎ 解：右图是一个蒙古包的示意图．‎ 根据题意，下部圆柱的底面积为‎12 m2‎．高h2＝‎1.8 m；上部圆锥的高h1＝3.2－1.8＝1.4(m)．‎ 圆柱的底面圆的半径r＝≈1.945(m)，侧面积为2π×1.945×1.8≈22.10(m2)．‎ 由由蒙古包表面积计算导入新课，激发学生学习本节知识的欲望 探究圆锥侧面积的计算方法 考查圆锥侧面积公式的应用 6‎ 教 学 过 程 ‎ ‎ 四、巩固练习：‎ 圆锥的母线长l＝≈2.404(m)，侧面展开扇形的弧长为2π×1.945≈12.28(m)，圆锥的侧面积为×2.404×12.28≈14.76(m2)．‎ 因此，搭建20个这样的的蒙古包至少需要毛毡20×(22.10＋14.76)≈738(m2)．‎ 三、 巩固练习：‎ ‎ ‎ 利用所学的新知识解决实际问题，考查学生对所学知识的应用能力。‎ ‎ ‎ 6‎ 小 结 ‎ ‎ ‎ 这节课你学到了什么？还有哪些困惑？‎ 板 书 设 计 ‎ ‎ ‎ 24．4弧长和扇形面积 ‎1．弧长的计算公式： 2．扇形的面积公式：S扇形＝ ‎ ‎ 或 S扇形＝lR．‎ ‎ 3、‎ 作 业 设 计 6‎ 教 学 反 思 6‎