高考数学专题复习教案： 解三角形应用举例 3页

解三角形应用举例 主标题：解三角形应用举例 副标题：为学生详细的分析解三角形应用举例的高考考点、命题方向以及规律总结。‎ 关键词：距离测量，高度测量，仰角，俯角，方位角，方向角 难度：3‎ 重要程度：5‎ 考点剖析：‎ 能够运用正弦定理、余弦定理等知识解决一些与测量和几何计算有关的实际问题．‎ 命题方向：‎ ‎1．测量距离问题是高考的常考内容，既有选择、填空题，也有解答题，难度适中，属中档题．‎ ‎2．高考对此类问题的考查常有以下两个命题角度：‎ ‎(1)测量问题；‎ ‎(2)行程问题．‎ 规律总结：‎ 1个步骤——解三角形应用题的一般步骤 ‎　‎ 2种情形——解三角形应用题的两种情形 ‎　(1)实际问题经抽象概括后，已知量与未知量全部集中在一个三角形中，可用正弦定理或余弦定理求解．‎ ‎(2)实际问题经抽象概括后，已知量与未知量涉及到两个或两个以上的三角形，这时需作出这些三角形，先解够条件的三角形，然后逐步求解其他三角形，有时需设出未知量，从几个三角形中列出方程(组)，解方程(组)得出所要求的解．‎ 2个注意点——解三角形应用题应注意的问题 ‎　(1)画出示意图后要注意寻找一些特殊三角形，如等边三角形、直角三角形、等腰三角形等，这样可以优化解题过程．‎ ‎(2)解三角形时，为避免误差的积累，应尽可能用已知的数据(原始数据)，少用间接求出的量．‎ 知 识 梳 理 ‎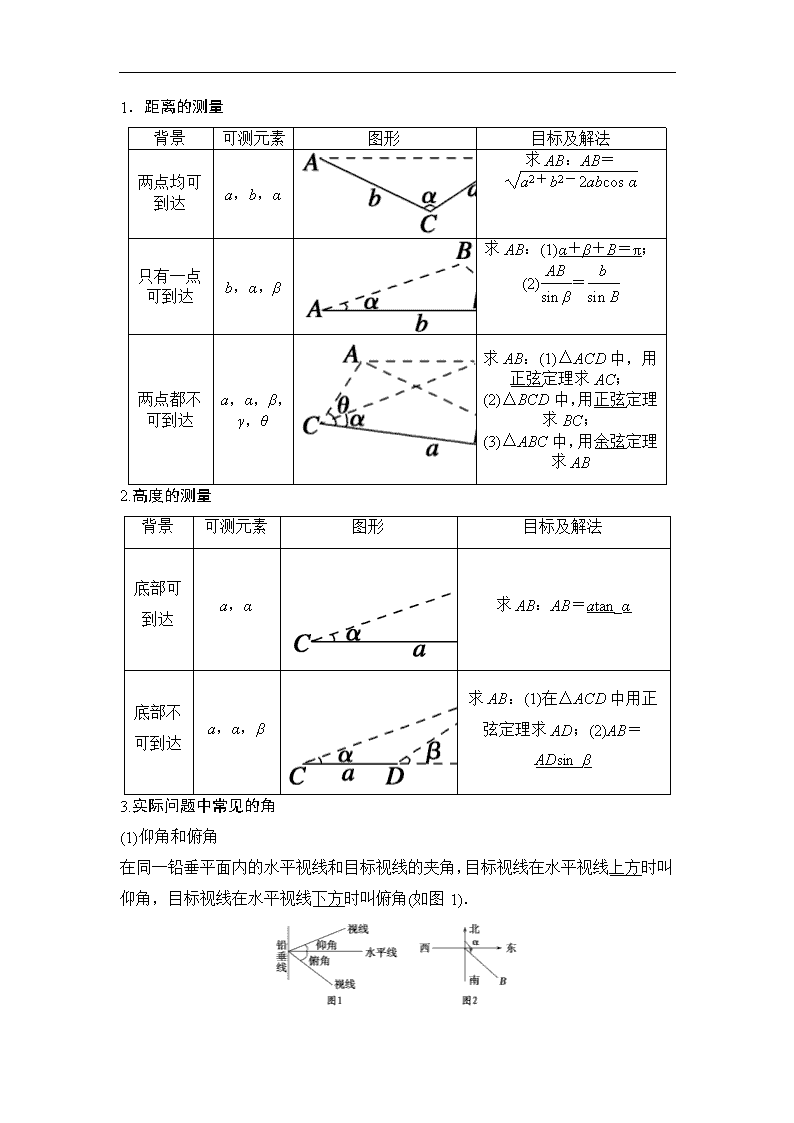1．距离的测量 背景 可测元素 图形 目标及解法 两点均可到达 a，b，α 求AB：AB＝ 只有一点可到达 b，α，β 求AB：(1)α＋β＋B＝π；(2)＝ 两点都不可到达 a，α，β，γ，θ 求AB：(1)△ACD中，用正弦定理求AC；‎ ‎(2)△BCD中，用正弦定理求BC；‎ ‎(3)△ABC中，用余弦定理求AB ‎2.高度的测量 背景 可测元素 图形 目标及解法 底部可到达 a，α 求AB：AB＝atan_α 底部不可到达 a，α，β 求AB：(1)在△ACD中用正弦定理求AD；(2)AB＝ADsin_β ‎3.实际问题中常见的角 ‎(1)仰角和俯角 在同一铅垂平面内的水平视线和目标视线的夹角，目标视线在水平视线上方时叫仰角，目标视线在水平视线下方时叫俯角(如图1)．‎ ‎(2)方位角 从正北方向起按顺时针转到目标方向线之间的水平夹角叫做方位角．如B点的方位角为α(如图2)．‎ ‎(3)方向角：正北或正南方向线与目标方向线所成的锐角，如南偏东30°，北偏西45°等．‎ ‎(4)坡度：坡面与水平面所成的二面角的度数．‎