高考数学复习 17-18版 第6章 第32课 复数 9页

第32课 复数 ‎[最新考纲]‎ 内容 要求 A B C 复数的概念 ‎√‎ 复数的四则运算 ‎√‎ 复数的几何意义 ‎√‎ ‎1．复数的有关概念 ‎(1)复数的概念：形如a＋bi(a，b∈R)的数叫复数，其中a，b分别是它的实部和虚部．若b＝0，则a＋bi为实数，若b≠0，则a＋bi为虚数，若a＝0且b≠0，则a＋bi为纯虚数．‎ ‎(2)复数相等：a＋bi＝c＋di⇔a＝c，b＝d(a，b，c，d∈R)．‎ ‎(3)共轭复数：a＋bi与c＋di共轭⇔a＝c，b＝－d(a，b，c，d∈R)．‎ ‎(4)复数的模：向量的模r叫作复数z＝a＋bi的模，即|z|＝|a＋bi|＝.‎ ‎2．复数的几何意义 复数z＝a＋bi复平面内的点Z(a，b)平面向量＝(a，b)．‎ ‎3．复数代数形式的四则运算 ‎(1)运算法则：设z1＝a＋bi，z2＝c＋di，a，b，c，d∈R.‎ z1±z2＝(a＋bi)±(c＋di)＝(a±c)＋(b±d)i.‎ z1·z2＝(a＋bi)(c＋di)＝(ac－bd)＋(bc＋ad)i.‎ ＝＝＋i(c＋di≠0)．‎ ‎(2)几何意义：复数加减法可按向量的平行四边形或三角形法则进行．‎ 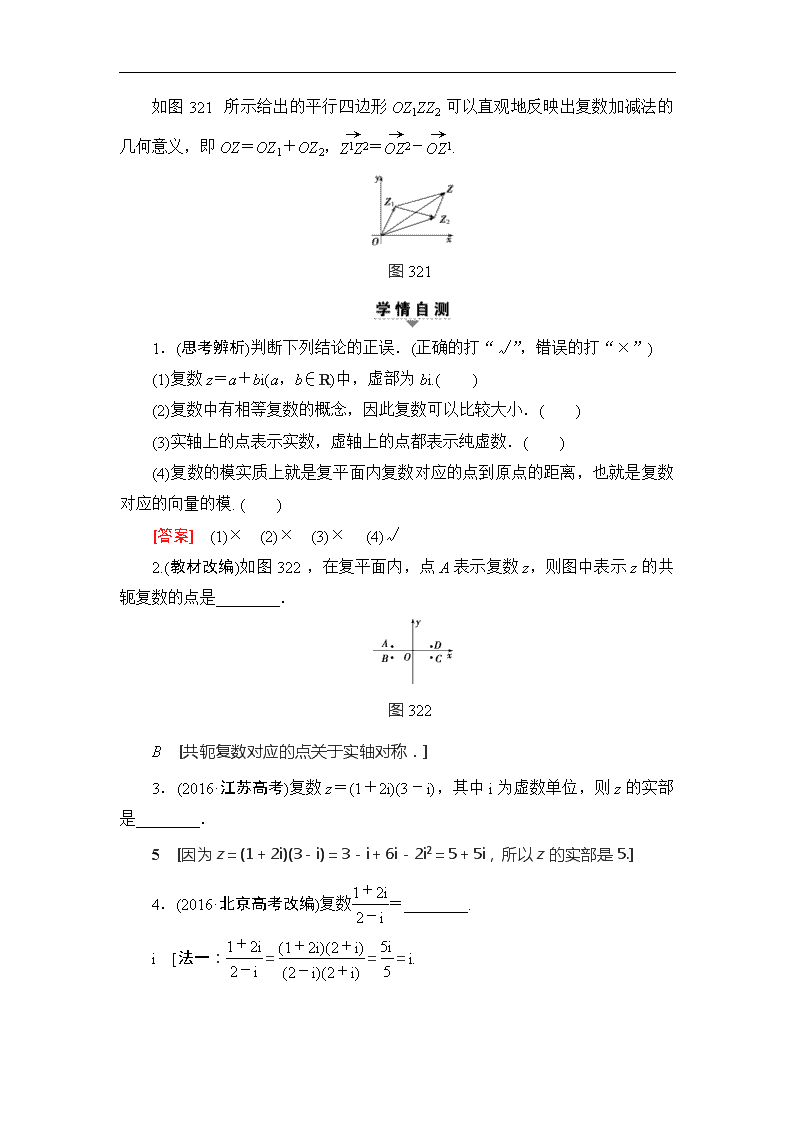如图321所示给出的平行四边形OZ1ZZ2可以直观地反映出复数加减法的几何意义，即OZ＝OZ1＋OZ2，＝－.‎ 图321‎ ‎1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎(1)复数z＝a＋bi(a，b∈R)中，虚部为bi.(　　)‎ ‎(2)复数中有相等复数的概念，因此复数可以比较大小．(　　)‎ ‎(3)实轴上的点表示实数，虚轴上的点都表示纯虚数．(　　)‎ ‎(4)复数的模实质上就是复平面内复数对应的点到原点的距离，也就是复数对应的向量的模. (　　)‎ ‎[答案]　(1)×　(2)×　(3)×　 (4)√‎ ‎2.(教材改编)如图322，在复平面内，点A表示复数z，则图中表示z的共轭复数的点是________．‎ 图322‎ B　[共轭复数对应的点关于实轴对称．]‎ ‎3．(2016·江苏高考)复数z＝(1＋2i)(3－i)，其中i为虚数单位，则z的实部是________．‎ ‎5　[因为z＝(1＋2i)(3－i)＝3－i＋6i－2i2＝5＋5i，所以z的实部是5.]‎ ‎4．(2016·北京高考改编)复数＝________.‎ i　[法一：＝＝＝i.‎ 法二：＝＝＝i.]‎ ‎5．(2015·江苏高考)设复数z满足z2＝3＋4i(i是虚数单位)，则z 的模为______．‎ 　[∵z2＝3＋4i，∴|z2|＝|z|2＝|3＋4i|＝＝5，‎ ‎∴|z|＝.]‎ 复数的有关概念 ‎　(2016·全国卷Ⅲ改编)若z＝1＋2i，则＝________.‎ i　[因为z＝1＋2i，则＝1－2i，所以z＝(1＋2i)(1－2i)＝5，则＝＝i.]‎ ‎(2)i是虚数单位，若复数(1－2i)(a＋i)是纯虚数，则实数a的值为________．‎ ‎－2　[由(1－2i)(a＋i)＝(a＋2)＋(1－2a)i是纯虚数可得a＋2＝0,1－2a≠0，解得a＝－2.]‎ ‎[规律方法]　1.解答与复数相关概念有关的问题时，需把所给复数化为代数形式，即a＋bi(a，b∈R)的形式，再根据题意列出实部、虚部满足的方程(组)即可．‎ ‎2．求复数模的常规思路是利用复数的有关运算先求出复数z，然后利用复数模的定义求解．‎ ‎[变式训练1]　(1)已知i为虚数单位，复数z＝的虚部为________. ‎ ‎【导学号：62172171】‎ ‎(2)(2017·泰州中学高三摸底考试)已知复数z满足(1＋i)·z＝－i，则的模为________．‎ ‎(1)　(2)　[(1)复数z＝＝＝＝＋i，则其虚部为.‎ ‎(2)(1＋i)·z＝－i⇒z＝＝⇒＝⇒||＝.‎ 复数代数形式的四则运算 ‎　(1)已知复数z满足(z－1)i＝1＋i，则z＝________.‎ ‎(2)(2016·天津高考)已知a，b∈R，i是虚数单位，若(1＋i)(1－bi)＝a，则的值为________．‎ ‎(1)2－i　(2)2　[(1)∵(z－1)i＝i＋1，∴z－1＝＝1－i，∴z＝2－i.‎ ‎(2)∵(1＋i)(1－bi)＝1＋b＋(1－b)i＝a，又a，b∈R，∴1＋b＝a且1－b＝0，得a＝2，b＝1，∴＝2.]‎ ‎[规律方法]　1.复数的加法、减法、乘法运算可以类比多项式运算，除法关键是分子分母同乘以分母的共轭复数，注意要把i的幂写成最简形式．‎ ‎2．记住以下结论，可提高运算速度 ‎(1)(1±i)2＝±2i；(2)＝i；(3)＝－i；(4)－b＋ai＝i(a＋bi)；(5)i4n＝1；i4n＋1＝i；i4n＋2＝－1；i4n＋3＝－i(n∈N)．‎ ‎[变式训练2]　(1)已知＝1＋i(i为虚数单位)，则复数z＝________.‎ ‎(2)已知i是虚数单位，8＋2 018＝________.‎ ‎(1)－1－i　(2)1＋i　[(1)由＝1＋i，得z＝＝＝＝－1－i.‎ ‎(2)原式＝8＋1 009‎ ‎＝i8＋1 009＝i8＋i1 009‎ ‎＝1＋i4×252＋1＝1＋i.]‎ 复数的几何意义 ‎　(1)(2016·全国卷Ⅱ改编)已知z＝(m＋3)＋(m－1)i在复平面内对应的点在第四象限，则实数m的取值范围是________．‎ ‎(2)设复数z1，z2在复平面内的对应点关于虚轴对称，z1＝2＋i，则z1z2＝________. 【导学号：62172172】‎ ‎(1)(－3,1)　(2)－5　[(1)由题意知即－3＜m＜1.故实数m的取值范围为(－3,1)．‎ ‎(2)∵z1＝2＋i在复平面内的对应点的坐标为(2,1)，又z1与z2在复平面内的对应点关于虚轴对称，则z2的对应点的坐标为(－2,1)，即z2＝－2＋i，‎ ‎∴z1z2＝(2＋i)(－2＋i)＝i2－4＝－5.]‎ ‎[规律方法]　1.复数z、复平面上的点Z及向量相互联系，即z＝a＋bi(a，b∈R)⇔Z(a，b)⇔.‎ ‎2．由于复数、点、向量之间建立了一一对应的关系，因此可把复数、向量与解析几何联系在一起，解题时可运用数形结合的方法，使问题的解决更加直观．‎ ‎[变式训练3]　定义运算＝ad－bc，则符合条件＝0的复数对应的点在第________象限．‎ 二　[由题意得z×2i－(1＋i)(－i)＝0，所以z＝＝－－i，则＝－＋i在复平面内对应的点为，位于第二象限．]‎ ‎[思想与方法]‎ ‎1．复数分类的关键是抓住z＝a＋bi(a，b∈R)的虚部：当b＝0时，z 为实数；当b≠0时，z为虚数；当a＝0，且b≠0时，z为纯虚数．‎ ‎2．复数除法的实质是分母实数化，其操作方法是分子、分母同乘以分母的共轭复数．‎ ‎3．化“虚”为“实”是解决复数问题的基本方法，其中，复数的代数形式是化“虚”为“实”的前提，复数相等的充要条件是化“虚”为“实”的桥梁．‎ ‎[易错与防范]‎ ‎1．判定复数是实数，仅注重虚部等于0是不够的，还需考虑它的实部是否有意义．‎ ‎2．两个虚数不能比较大小．‎ ‎3．利用复数相等a＋bi＝c＋di列方程时，应注意a，b，c，d∈R的前提条件．‎ ‎4．注意不能把实数集中的所有运算法则和运算性质照搬到复数集中来．例如，若z1，z2∈C，z＋z＝0，就不能推出z1＝z2＝0；z2<0在复数范围内有可能成立．‎ 课时分层训练(三十二)‎ A组　基础达标 ‎(建议用时：30分钟)‎ ‎1．(2017·苏州模拟)设复数zi＝1＋2i(i是虚数单位)，则z＝________.‎ ‎2－i　[由zi＝1＋2i得z＝＝＝＝2－i.]‎ ‎2．(2017·苏锡常镇二模)已知(a－i)2＝2i，其中i是虚数单位，那么实数a＝________. 【导学号：62172173】‎ ‎－1　[由(a－i)2＝2i得a2－1－2ai＝2i，故即a＝－1.]‎ ‎3．(2017·无锡模拟)若复数z满足(2－i)z＝4＋3i(i为虚数单位)，则|z|＝________.‎ 　[由(2－i)z＝4＋3i，得|(2－i)z|＝|4＋3i|，‎ 即|z|＝5，∴|z|＝.]‎ ‎4．(2016·全国卷Ⅰ改编)设(1＋2i)(a＋i)的实部与虚部相等，其中a 为实数，则a＝________.‎ ‎－3　[(1＋2i)(a＋i)＝a－2＋(1＋2a)i，由题意知a－2＝1＋2a，解得a＝－3.]‎ ‎5．(2016·全国卷Ⅰ改编)设(1＋i)x＝1＋yi，其中x，y是实数，则|x＋yi|＝________.‎ 　[∵(1＋i)x＝1＋yi，∴x＋xi＝1＋yi.‎ 又∵x，y∈R，∴x＝1，y＝x＝1.‎ ‎∴|x＋yi|＝|1＋i|＝.]‎ ‎6．(2017·泰州期末)如图323，在复平面内，点A对应的复数为z1，若＝i(i为虚数单位)，则z2＝________.‎ 图323‎ ‎－2－i　[由图可知，z1＝－1＋2i，‎ ‎∴z2＝z1i＝(－1＋2i)·i＝－i－2.]‎ ‎7．(2017·南京模拟)设＝a＋bi(i为虚数单位，a，b∈R)，则a＋b＝________.‎ ‎1　[∵＝＝＝2－i.‎ 又由a＋bi＝2－i可知 ，a＝2，b＝－1，‎ ‎∴a＋b＝2－1＝1.]‎ ‎8．(2017·苏州模拟)复数z＝(a<0)，其中i为虚数单位，|z|＝，则a的值为________. 【导学号：62172174】‎ ‎－5　[∵z＝，且|z|＝，‎ ‎∴＝，∴a＝－5.]‎ ‎9．若z＝4＋3i，则＝________.‎ －i　[∵z＝4＋3i，∴＝4－3i，|z|＝＝5，‎ ‎∴＝＝－i.]‎ ‎10．已知复数z＝1＋，则1＋z＋z2＋…＋z2 019＝________.‎ ‎0　[z＝1＋＝1＋＝i，∴1＋z＋z2＋…＋z2 019＝＝＝＝0.]‎ ‎11．已知a∈R，若为实数，则a＝________.‎ ‎－　[＝＝＝＋i.‎ ‎∵为实数，∴＝0，∴a＝－.]‎ ‎12．已知复数z＝x＋yi，且|z－2|＝，则的最大值为________. ‎ ‎【导学号：62172175】‎ 　[∵|z－2|＝＝，‎ ‎∴(x－2)2＋y2＝3.‎ 由图可知max＝＝.]‎ B组　能力提升 ‎(建议用时：15分钟)‎ ‎1．已知复数z1＝－＋i，z2＝－－i，则下列命题中错误的是________．(填序号)‎ ‎①z＝z2；‎ ‎②|z1|＝|z2|；‎ ‎③z－z＝1；‎ ‎④z1，z2互为共轭复数．‎ ‎③　[依题意，注意到z＝2＝－i＝－－i＝z2，因此①正确；注意到|z1|＝1＝|z2|，因此②正确；注意到＝－－i＝z2，因此④正确；注意到z＝z·z1＝2·＝＝1，同理z＝1，因此z－z＝0，③错误．]‎ ‎2．设f(n)＝n＋n(n∈N＋)，则集合{f(n)}中元素的个数为________．‎ ‎3　[f(n)＝n＋n＝in＋(－i)n，‎ f(1)＝0，f(2)＝－2，f(3)＝0，f(4)＝2，f(5)＝0，…，‎ ‎∴集合中共有3个元素．]‎ ‎3．已知集合M＝{1，m,3＋(m2－‎5m－6)i}，N＝{－1,3}，若M∩N＝{3}，则实数m的值为________．‎ ‎3或6　[∵M∩N＝{3}，∴3∈M且－1∉M，‎ ‎∴m≠－1,3＋(m2－5m－6)i＝3或m＝3，‎ ‎∴m2－5m－6＝0且m≠－1或m＝3，‎ 解得m＝6或m＝3.]‎ ‎4．已知复数z1＝cos 15°＋sin 15°i和复数z2＝cos 45°＋sin 45°i，则z1·z2＝________.‎ ＋i　[z1·z2＝(cos 15°＋sin 15°i)(cos 45°＋sin 45°i)＝(cos 15°cos 45°－sin 15°sin 45°)＋(sin 15°cos 45°＋cos 15°sin 45°)i＝cos 60°＋sin 60°i＝＋i.]‎