高考数学专题复习教案： 二元一次不等式(组)与简单的线性规划备考策略 6页

二元一次不等式(组)与简单的线性规划问题备考策略 主标题：二元一次不等式(组)与简单的线性规划问题备考策略 副标题：通过考点分析高考命题方向，把握高考规律，为学生备考复习打通快速通道。‎ 关键词：不等式，二元一次不等式(组)与简单的线性规划问题，备考策略 难度：2‎ 重要程度：5‎ 内容：‎ ‎1.画出不等式组表示的平面区域?‎ 思维规律解题 考点1 二元一次不等式(组)与平面区域 例1.若实数满足不等式组，则点所组成的平面区域的面积为 ．‎ ‎【答案】‎ ‎【解析】不等式组表示的平面区域如图中的三角形（包括边界），解方程组可得，对，令得，即，对，令得，即，‎ 所以点所组成的平面区域的面积为．‎ 例2.若实数，满足约束条件，已知点所表示的平面区域为三角形，则实数的取值范围为 ‎ ‎【答案】‎ ‎【解析】作出可行域如图所示：‎ 由得：，所以点的坐标为，要使所表示的平面区域为三角形，则点必须在直线的下方，所以，即，所以实数的取值范围是．‎ 考点2 线性规划中目标函数的最值问题 例3.已知实数，满足则的最小值为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】不等式组表示的平面区域如图中的三角形（包括边界），解方程组可得，平移直线，当经过点时取得最小值.‎ 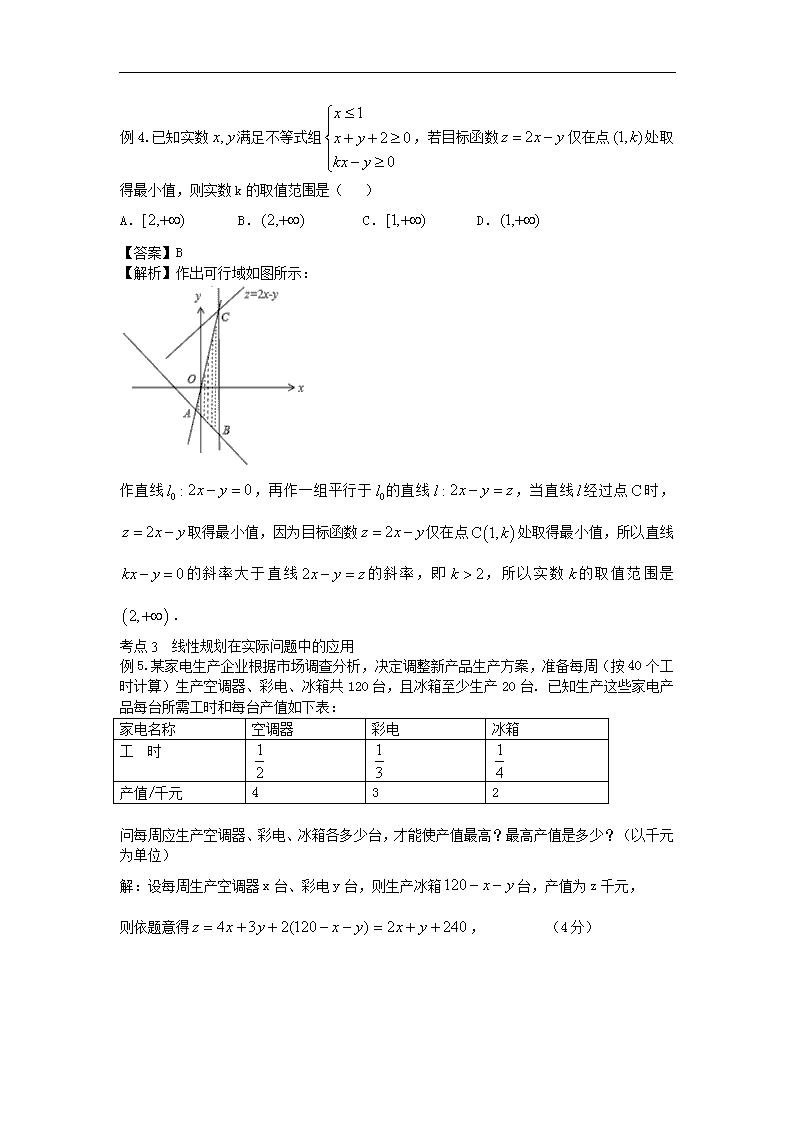例4.已知实数满足不等式组，若目标函数仅在点处取得最小值，则实数k的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】作出可行域如图所示：‎ 作直线，再作一组平行于的直线，当直线经过点时，取得最小值，因为目标函数仅在点处取得最小值，所以直线的斜率大于直线的斜率，即，所以实数的取值范围是．‎ 考点3 线性规划在实际问题中的应用 例5.某家电生产企业根据市场调查分析，决定调整新产品生产方案，准备每周（按40个工时计算）生产空调器、彩电、冰箱共120台，且冰箱至少生产20台. 已知生产这些家电产品每台所需工时和每台产值如下表：‎ 家电名称 空调器 彩电 冰箱 工 时 产值/千元 ‎4‎ ‎3‎ ‎2‎ 问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？（以千元为单位）‎ 解：设每周生产空调器x台、彩电y台，则生产冰箱台，产值为z千元，‎ 则依题意得， （4分）‎ 且x，y满足即 （8分）‎ 可行域如图所示. （10分）‎ 解方程组得 即M（10，90）.（11分） ‎ 让目标函数表示的直线在可行域上平移，‎ 可得在M（10，90）处取得最大值，且 ‎（千元）. （13分）‎ 答：每周应生产空调器10台，彩电90台，冰箱20台，才能使产值最高，最高产值是350千元.（14分） ‎ 考点4 求非线性目标函数的最大（小）值 例6.已知实数、满足,若存在、满足，则的最小值为（ ）‎ A．1 B． C． D．‎ ‎【答案】B ‎【解析】可行域为直线围成的三角形区域，到点的距离最小值为，所以的最小值为 例7.设不等式组所表示的平面区域是，平面区域与关于直线对称，对于中的任意一点与中的任意一点的最小值等于（ ）‎ A.2 B.4 C. D.‎ ‎【答案】B ‎【解析】由题意知，所求的的最小值，即为区域中的点到直线的距离的最小值的两倍，画出已知不等式表示的平面区域，如图所示，‎ 可得点 到直线的距离最小，故的最小值为，所以选B.‎ 例8.已知，满足条件，则的最小值（ ）‎ ‎ A． B． C． D．4‎ ‎【答案】B．‎ ‎【解析】根据题意，画出不等式组所表示的区域，即可行域，而，‎ 可看成区域内一点与点连线的斜率，从而可知，‎ ‎，∴，故选B．‎