2019年高考数学总复习检测第27讲　函数y＝Asin(ωx＋φ)的图象与性质 5页

第27讲　函数y＝Asin(ωx＋φ)的图象与性质 ‎1．已知函数f(x)＝sin(ωx＋)(ω>0)的最小正周期为π，则该函数的图象(A)‎ A．关于点(，0)对称 B．关于直线x＝对称 C．关于点(，0)对称 D．关于直线x＝对称 ‎ 由题意知ω＝2，所以f(x)＝sin(2x＋)，将x＝代入，得f()＝0，所以选A.‎ ‎2．将函数y＝sin(2x＋φ)的图象沿x轴向左平移个单位后，得到一个偶函数的图象，则φ的一个可能取值为(B)‎ A. B. C．0 D．－ ‎ y＝sin(2x＋φ)的图象沿x轴向左平移个单位后变为函数y＝sin[2(x＋)＋φ]＝sin(2x＋＋φ)的图象，‎ 又y＝sin(2x＋＋φ)为偶函数，‎ 所以＋φ＝＋kπ(k∈Z)，‎ 所以φ＝＋kπ(k∈Z)，若k＝0，则φ＝.‎ ‎3．(2016·河北衡水模拟(三))为了得到 y＝sin(x＋)的图象，可将函数y＝sin x的图象向左平移m个单位长度或向右平移n个单位长度(m，n为正数)，则|m－n|的最小值为(A)‎ A.π B.π ‎ C.π D.π ‎ y＝sin x向左平移m个单位长度，得到y＝sin(x＋), 所以m＝＋2k1π(k1∈Z)，‎ y＝sin x向右平移n个单位长度，得到y＝sin(x＋)，所以n＝π＋2k2π(k2∈Z) ，‎ 所以|m－n|最小值即|＋2k1π－π－2k2π|＝|－π＋2(k1－k2)π| 的最小值．‎ 当k1－k2＝1时， |m－n|的最小值为|2π－π|＝π，‎ 所以所求的最小值是π.‎ ‎4．(2016·石家庄市一模)函数f(x)＝Asin(ωx＋φ)(A>0，ω>0)的部分图象如下图所示，则f()的值为(D)‎ A．－ B．－ C．－ D．－1‎ ‎ 显然A＝，＝－＝，‎ 所以T＝π，所以ω＝2，则f(x)＝sin(2x＋φ)，‎ 因为f(x)的图象经过点(，0)，‎ 结合正弦函数的图象特征知，2×＋φ＝2kπ＋π，k∈Z，‎ 所以φ＝2kπ＋，k∈Z.‎ 所以f(x)＝sin(2x＋2kπ＋)，k∈Z，‎ 所以f()＝sin(＋2kπ＋)＝sin(2kπ＋π＋)＝－sin＝－1，k∈Z.故选D.‎ ‎5．直线y＝a(a为常数)与函数y＝tan ωx(ω为常数且ω>0)的图象相交的相邻两点间的距离是　　.‎ ‎ 直线y＝a与曲线y＝tan ωx相邻两点间的距离就是此曲线的一个最小正周期，为.‎ ‎6．(2013·新课标卷Ⅱ)函数y＝cos(2x＋φ)(－π≤φ<π)的图象向右平移个单位后，与函数y＝sin(2x＋)的图象重合，则φ＝　　.‎ ‎ 将y＝cos(2x＋φ)的图象向右平移个单位后，得到y＝cos[2(x－)＋φ]＝cos(2x－π＋φ)＝sin(2x－π＋φ＋)＝sin(2x＋φ－)，‎ 而它与函数y＝sin(2x＋)的图象重合，‎ 令2x＋φ－＝2x＋＋2kπ(k∈Z)，‎ 得φ＝＋2kπ(k∈Z)．‎ 又－π≤φ<π，故φ＝.‎ ‎7．已知函数f(x)＝3sin(＋)＋3.‎ ‎(1)指出f(x)的周期、振幅、初相、对称轴；‎ ‎(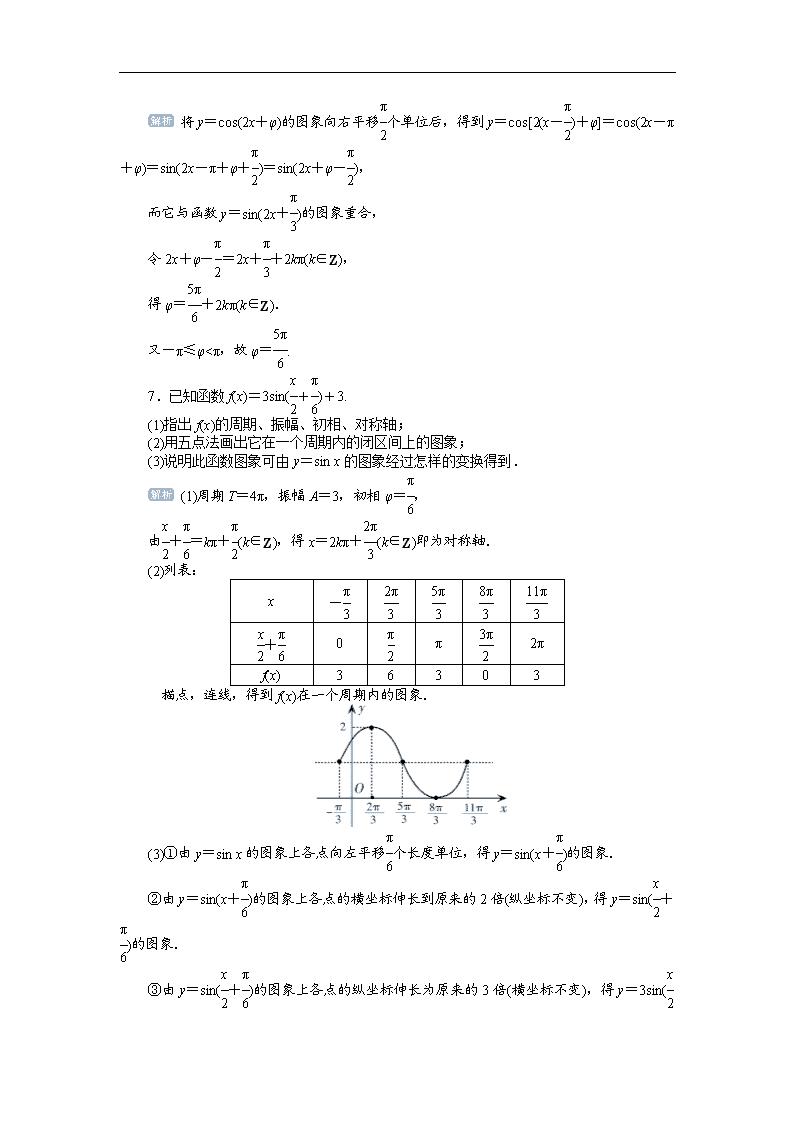2)用五点法画出它在一个周期内的闭区间上的图象；‎ ‎(3)说明此函数图象可由y＝sin x的图象经过怎样的变换得到．‎ ‎ (1)周期T＝4π，振幅A＝3，初相φ＝，‎ 由＋＝kπ＋(k∈Z)，得x＝2kπ＋(k∈Z)即为对称轴．‎ ‎(2)列表：‎ x ‎－ ＋ ‎0‎ π ‎2π f(x)‎ ‎3‎ ‎6‎ ‎3‎ ‎0‎ ‎3‎ ‎　描点，连线，得到f(x)在一个周期内的图象．‎ ‎(3)①由y＝sin x的图象上各点向左平移个长度单位，得y＝sin(x＋)的图象．‎ ‎②由y＝sin(x＋)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，得y＝sin(＋)的图象．‎ ‎③由y＝sin(＋)的图象上各点的纵坐标伸长为原来的3倍(横坐标不变)，得y＝3sin(＋)的图象．‎ ‎④由y＝3sin(＋)的图象上各点向上平移3个长度单位，得y＝3sin(＋)＋3的图象．‎ ‎8．(2017·天津卷)设函数f(x)＝2sin(ωx＋φ)，x∈R，其中ω>0，|φ|<π.若f()＝2，f()＝0，且f(x)的最小正周期大于2π，则(A)‎ A．ω＝，φ＝ B．ω＝，φ＝－ C．ω＝，φ＝－ D．ω＝，φ＝ ‎ 因为f()＝2，f()＝0，且f(x)的最小正周期大于2π，‎ 所以f(x)的最小正周期为4(π－π)＝3π，‎ 所以ω＝＝，所以f(x)＝2sin(x＋φ)．‎ 因为f()＝2，‎ 所以2sin(×π＋φ)＝2，得φ＝2kπ＋，k∈Z.‎ 又|φ|＜π，所以取k＝0，得φ＝.‎ ‎9．(2016·郑州市二模)将函数f(x)＝－cos 2x的图象向右平移个单位后得到函数g(x)，则 g(x)具有性质：‎ ‎①最大值为1，图象关于直线x＝对称；‎ ‎②在(0，)上单调递减，为奇函数；‎ ‎③在(－，)上单调递增，为偶函数；‎ ‎④周期为π，图象关于点(，0)对称．‎ 其中正确的命题的序号是　②　.‎ ‎ 由题意得函数g(x)＝－cos(2x－2×)＝－sin 2x，‎ 对于①，将x＝代入，g(x)不取最值，故①不正确．‎ 对于②，易知其为奇函数，‎ 由2kπ－<2x<2kπ＋(k∈Z)，‎ 得kπ－