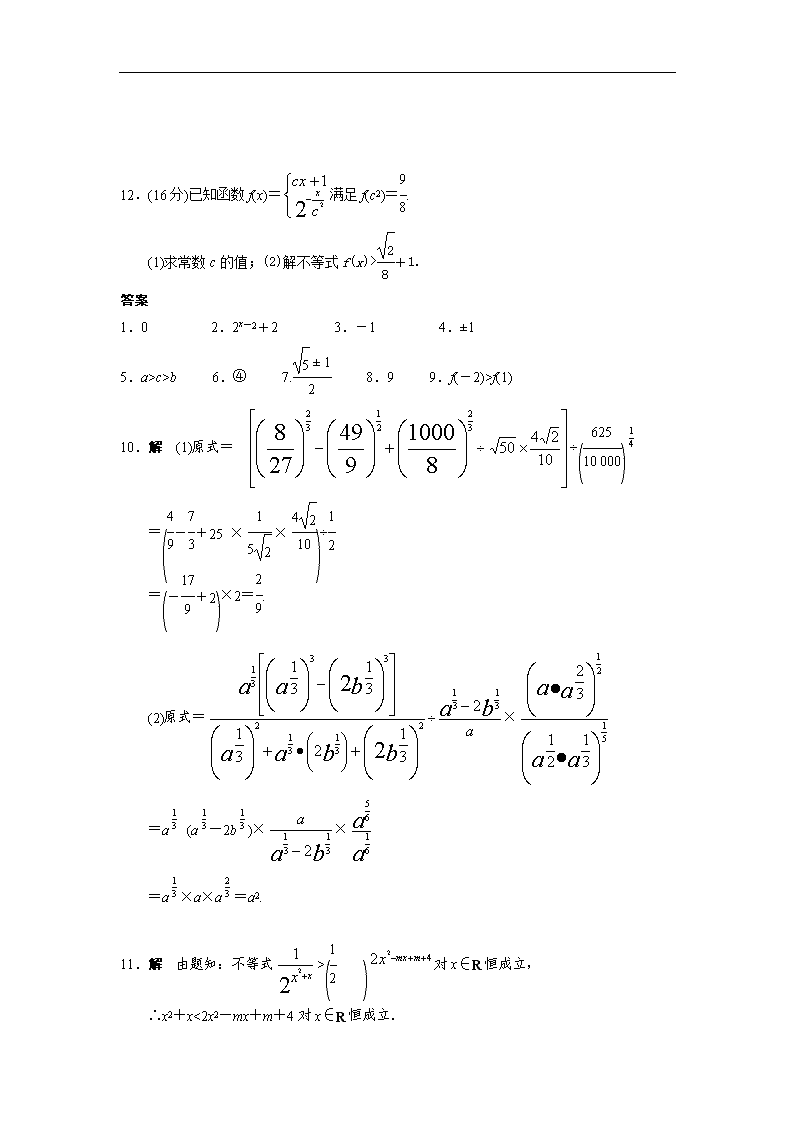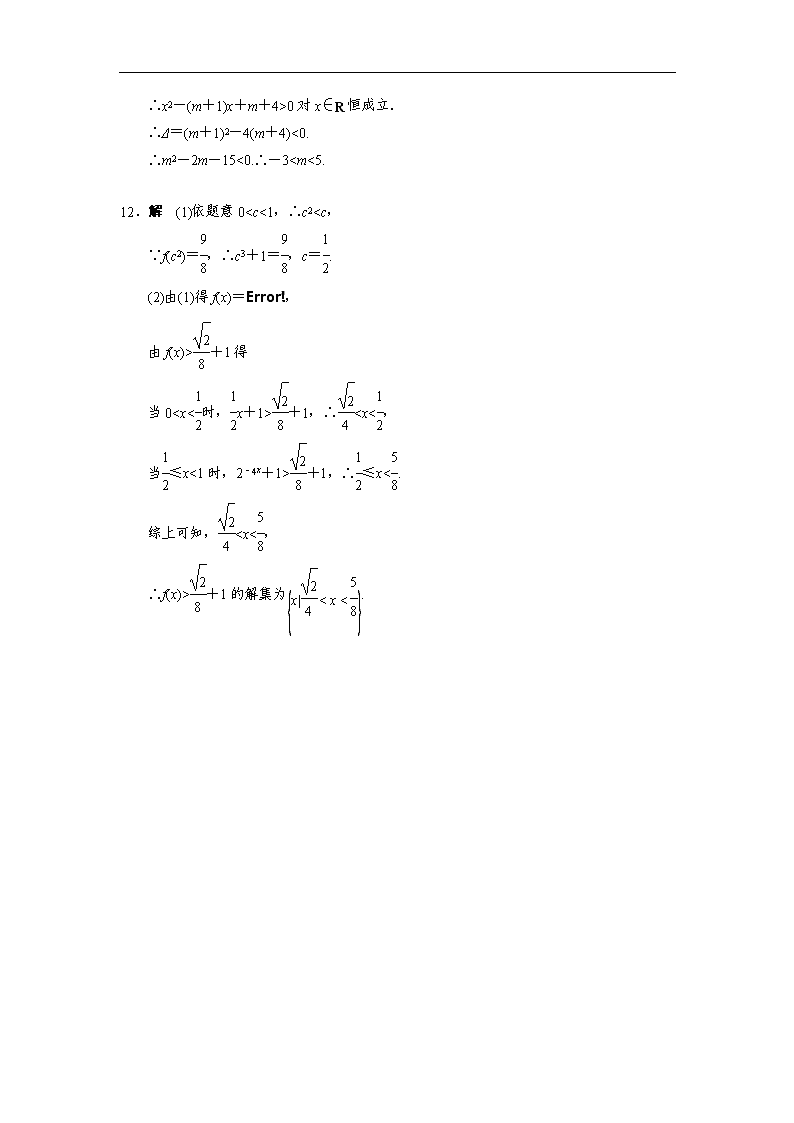高考数学复习练习试题2_4指数与指数函数 3页

‎§2.4　指数与指数函数 一、填空题(本大题共9小题，每小题6分，共54分)‎ ‎1．(2010·扬州一模)下列等式＝2a；＝；－3＝中一定成立的有________个．‎ ‎2．把函数y＝f(x)的图象向左、向下分别平移2个单位长度得到函数y＝2x的图象，则f(x)＝__________.‎ ‎3．设f(x)是定义在R上的奇函数，且当x>0时，f(x)＝2x－3，则f(－2)＝________.‎ ‎4．若函数f(x)＝ (a为常数)在定义域上为奇函数，则a的值为________．‎ ‎5．(2010·安徽改编)设a＝，b＝，c＝，则a，b，c的大小关系是____________．‎ ‎6．(2010·徐州模拟)已知函数f(x)＝|2x－1|，af(c)>f(b)，则下列结论中，一定成立的是________．‎ ‎①a<0，b<0，c<0; ②a<0，b≥0，c>0；‎ ‎③2－a<2c; ④2a＋2c<2.‎ ‎7．若指数函数y＝ax 在[－1,1]上的最大值与最小值的差是1，则底数a＝________.‎ ‎8．函数f(x)＝(a>1)恒过点(1,10)，则m＝________.‎ ‎9．(2010·南通调研)设函数f(x)＝a－|x| (a>0且a≠1)，若f(2)＝4，则f(－2)与f(1)的大小关系是__________．‎ 二、解答题(本大题共3小题，共46分)‎ ‎10．(14分)(1)计算：[－0.5＋(0.008)÷(0.02)×(0.32)]÷0.062 50.25；‎ ‎(2)化简：÷×(式中字母都是正数)‎ ‎11.(16分)已知对任意x∈R，不等式>恒成立，求实数m的取值范围．‎ ‎12．(16分)已知函数f(x)＝满足f(c2)＝.‎ ‎(1)求常数c的值；(2)解不等式f(x)>＋1.‎ 答案 ‎1．0 2．2x－2＋2 3．－1 4．±1 ‎ ‎5．a>c>b 6．④ 7. 8．9 9．f(－2)>f(1)‎ ‎10．解　(1)原式＝÷ ‎＝÷ ‎＝×2＝.‎ ‎(2)原式＝÷×‎ ‎＝a (a－2b)××‎ ‎＝a×a×a＝a2.‎ ‎11．解　由题知：不等式>对x∈R恒成立，‎ ‎∴x2＋x<2x2－mx＋m＋4对x∈R恒成立．‎ ‎∴x2－(m＋1)x＋m＋4>0对x∈R恒成立．‎ ‎∴Δ＝(m＋1)2－4(m＋4)<0.‎ ‎∴m2－2m－15<0.∴－3＋1得 当0＋1，∴＋1，∴≤x<.‎ 综上可知，＋1的解集为.‎