备战2014高考数学 高频考点归类分析（真题为例）：传统概率的计算 10页

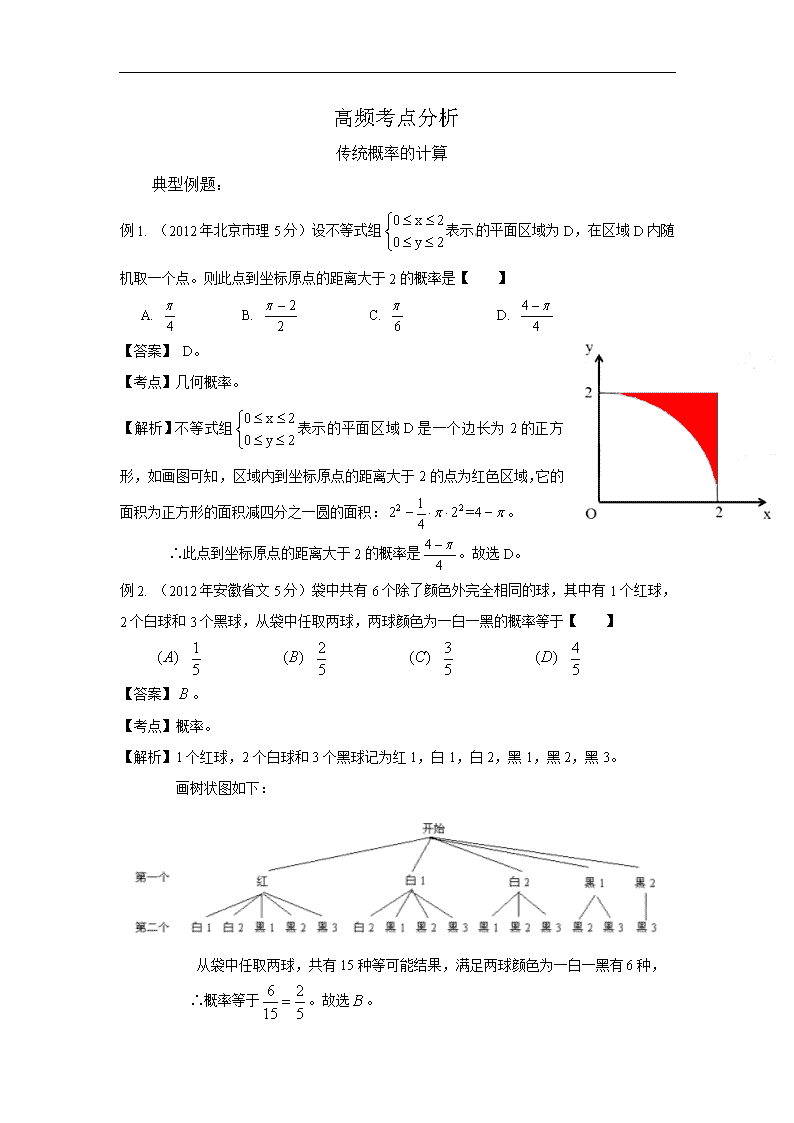
高频考点分析 传统概率的计算 典型例题： ‎ 例1. （2012年北京市理5分）设不等式组表示的平面区域为D，在区域D内随机取一个点。则此点到坐标原点的距离大于2的概率是【 】‎ A. B. C. D. [来源:Zxxk.Com]‎ ‎【答案】 D。‎ ‎【考点】几何概率。‎ ‎【解析】不等式组表示的平面区域D是一个边长为2的正方形，如画图可知，区域内到坐标原点的距离大于2的点为红色区域，它的面积为正方形的面积减四分之一圆的面积：。‎ ‎ ∴此点到坐标原点的距离大于2的概率是。故选D。‎ 例2. （2012年安徽省文5分）袋中共有6个除了颜色外完全相同的球，其中有1个红球，2个白球和3个黑球，从袋中任取两球，两球颜色为一白一黑的概率等于【 】‎ ‎ ‎ ‎【答案】。‎ ‎【考点】概率。‎ ‎【解析】1个红球，2个白球和3个黑球记为红1，白1，白2，黑1，黑2，黑3。‎ ‎ 画树状图如下：‎ 从袋中任取两球，共有15种等可能结果，满足两球颜色为一白一黑有种，‎ ‎∴概率等于。故选。‎ 例3. （2012年广东省理5分）从概率位数与十位数之和为奇数的两位数中任取一个，其个位数为0的概率是【　　】‎ A. B. C. D. ‎ ‎【答案】D。‎ ‎【考点】分类讨论的思想，概率。‎ ‎【解析】由题意知，个位数与十位数应该一奇一偶。‎ ‎①个位数为奇数，十位数为偶数共有5×5=25个两位数；‎ ‎②个位数为偶数，十位数为奇数共有5×4=20个两位数。‎ 两类共有25+20=45个数，其中个位数为0，十位数为奇数的有10,30,50,70,90共5个数。‎ ‎∴概率位数为0的概率是=。故选D。‎ 例4. （2012年湖北省理5分）如图，在圆心角为直角的扇形OAB中，分别以OA，OB为直径作两个半圆。在扇形OAB内随机取一点，则此点取自阴影部分的概率是【 】‎ A. B. C. D.‎ ‎【答案】A。‎ ‎【考点】概率，扇形面积，特殊元素法。‎ ‎【解析】取大圆的半径为2，则小圆半径为1，‎ ‎ 如图，两个半圆相交的阴影部分是两个弓形，连接OC，取OA的中点D，连接CD。‎ ‎ ∴两个半圆相交的阴影部分面积为。‎ 又∵扇形OAB的面积为，‎ ‎∴阴影部分的面积为。‎ 在扇形OAB内随机取一点，则此点取自阴影部分的概率。故选A。‎ 例5. （2012年福建省理5分）如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为【 】‎ A. B. C. D. ‎【答案】C。‎ ‎【考点】定积分的计算，几何概型的计算。‎ ‎【解析】∵，‎ ‎ ∴利用几何概型公式得：。故选C。[来源:学科网ZXXK]‎ 例6. （2012年辽宁省理5分）在长为‎12cm的线段AB上任取一点C.现作一矩形，领边长分别等于线段AC，CB的长，则该矩形面积小于‎32cm2的概率为【 】[来源:学科网]‎ ‎(A) (B) (C) (D) ‎ ‎【答案】C。‎ ‎【考点】函数模型的应用、不等式的解法、几何概型的计算。‎ ‎【解析】设线段AC的长为cm，则线段CB的长为()cm。那么矩形的面积为cm2。‎ 由，解得。又，所以该矩形面积小于‎32cm2的概率为。故选C。‎ 例7. （2012年辽宁省文5分）在长为‎12cm的线段AB上任取一点C. ‎ 现作一矩形，邻边长分别等于线段AC,CB的长，则该矩形面积大于‎20cm2的概率为【 】‎ ‎:(A) (B) (C) (D) ‎ ‎【答案】C。‎ ‎【考点】函数模型的应用、不等式的解法、几何概型的计算 ‎【解析】设线段AC的长为cm，则线段CB的长为()cm,那么矩形的面积为cm2，由，解得。又，所以该矩形面积大于‎20cm2的概率为。故选C。‎ 例8. （2012年上海市文4分）三位同学参加跳高、跳远、铅球项目的比赛，若每人都选择其中两个项目，则有且仅有两人选择的项目完全相同的概率是 ▲ （结果用最简分数表示）.‎ ‎【答案】。‎ ‎【考点】排列组合概率问题（古典概型）。‎ ‎【解析】设概率，则。‎ 求k，分三步：①选二人，让他们选择的项目相同，有种；②确定上述二人所选择的相同的项 目，有种；③确定另一人所选的项目，有种. 所以，故。‎ 例9. （2012年湖南省理5分）函数的导函数的部分图像如图所示，其中，P为图像与y轴的交点，A,C为图像与轴的两个交点，B为图像的最低点.[来源:学科网ZXXK]‎ ‎（1）若，点P的坐标为，则 ▲ ;‎ ‎（2）若在曲线段与轴所围成的区域内随机取一点，则该点在△ABC内的概率为 ▲ .‎ ‎【答案】（1）3；（2）。‎ ‎【考点】三角函数的图像与性质，定积分，几何概率。‎ ‎【解析】（1），当，点P的坐标为时，，‎ ‎ ∴。‎ ‎（2）由图知，。‎ ‎∵，∴曲线段与轴所围成的区域面积为 ‎。‎ 由几何概率知该点在△ABC内的概率为。‎ 例10. （2012年浙江省文5分）从边长为1的正方形的中心和顶点这五点中，随机（等可能）取两点，则 该两点间的距离为的概率是 ▲ 。‎ ‎【答案】。‎ ‎【考点】随机事件的概率。‎ ‎【解析】从边长为1的正方形的中心和顶点这五点中，随机（等可能）取两点共有=10‎ 种，若使两点间的距离为，则为对角线一半，选择点必含中心，共有4种可能。故该两点间的距离为的概率是。‎ 例11. （2012年重庆市文5分）某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其它三门艺术课各1节，则在课表上的相邻两节文化课之间至少间隔1节艺术课的概率为 ▲ （用数字作答）。‎ ‎【答案】。‎ ‎【考点】列举法计算基本事件数及事件发生的概率，古典概型及其概率计算公式。‎ ‎【分析】语文、数学、外语三门文化课两两不相邻的排法可分为两步，先把其它三门艺术课排列有种排法，第二步把语文、数学、外语三门文化课插入由那三个隔开的四个空中，有 种排法，‎ ‎∴所有的排法种数为 =144。‎ ‎∴在课表上的相邻两节文化课之间至少间隔1节艺术课的概率为。 ‎ 例12. （2012年重庆市理5分）某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课个1节，则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 ▲ （用数字作答）.‎ ‎【答案】。‎ ‎【考点】排列数公式及概率。‎ ‎【分析】随意安排6节课的方法数为，‎ 而“相邻两节文化课之间最多间隔1节艺术课”的对立事件为“相邻两节文化课之间排3节艺术课或排2节艺术课”，共有。‎ ‎∴其概率为。‎ 例13. （2012年江苏省5分）现有10个数，它们能构成一个以1为首项，为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是 ▲ ．‎ ‎【答案】。‎ ‎【考点】等比数列，概率。‎ ‎【解析】∵以1为首项，为公比的等比数列的10个数为1，－3，9，-27，···其中有5个负数，1个正数1计6个数小于8，‎ ‎ ∴从这10个数中随机抽取一个数，它小于8的概率是。‎ 例14. （2012年山东省文12分）袋中有五张卡片，其中红色卡片三张，标号分别为1，2，3；蓝色卡片两张，标号分别为1，2.[来源:Z+xx+k.Com]‎ ‎(Ⅰ)从以上五张卡片中任取两张，求这两张卡片颜色不同且标号之和小于4的概率；‎ ‎(Ⅱ)现袋中再放入一张标号为0的绿色卡片，从这六张卡片中任取两张，求这两张卡片颜色不同且标 号之和小于4的概率.‎ ‎【答案】解：(Ⅰ)画树状图：‎ ‎ ∵图中可见，从五张卡片中任取两张的所有等可能情况有10种，其中两张卡片的颜色不同且标号之和小于4的有3种情况，‎ ‎ ∴这两张卡片颜色不同且标号之和小于4的概率为。‎ ‎(Ⅱ) 画树状图：‎ ‎ ∵图中可见，从六张卡片中任取两张的所有等可能情况有15种，其中两张卡片的颜色不同且标号之和小于4的有8种情况，‎ ‎ ∴这两张卡片颜色不同且标号之和小于4的概率为。‎ ‎【考点】概率。‎ ‎【解析】(Ⅰ)画树状图，找出从五张卡片中任取两张的所有等可能情况和其中两张卡片的颜色不同且标号之和小于4的情况，即可求出概率。‎ ‎(Ⅱ)画树状图，找出从六张卡片中任取两张的所有等可能情况和其中两张卡片的颜色不同且标号之和小于4的情况，即可求出概率。‎ 例15. （2012年江西省文12分）如图，从，，，，，这个点中随机选取个点。‎ （1） 求这3点与原点恰好是正三棱锥的四个顶点的概率；‎ （2） 求这3点与原点共面的概率。‎ ‎【答案】解：（1）∵总的结果数为20种，满足条件的种数为2种：，‎ ‎∴所求概率为。‎ ‎（2）∵满足条件的情况为,,,,,‎ ‎，‎ ‎∴所求概率为。‎ ‎【考点】概率。‎ ‎【解析】根据概率的求法，找准两点：①全部等可能情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率。‎ 例16. （2012年福建省文12分）在等差数列{an}和等比数列{bn}中，a1＝b1＝1，b4＝8，{an}的前10项和S10＝55.‎ ‎（I）求an和bn；‎ ‎（II）现分别从{an}和{bn}的前3项中各随机抽取一项，写出相应的基本事件，并求这两项的值相等的概率．‎ ‎【答案】解：（I）设{an}的公差为d，{bn}的公比为q.依题意得S10＝10＋d＝55，b4＝q3＝8，‎ 解得d＝1，q＝2，所以an＝n，bn＝2n－1。‎ ‎（II）分别从{an}，{bn}的前3项中各随机抽取一项，得到的基本事件有9个：(1,1)，(1,2)，(1,4)，(2,1)，(2,2)，(2,4)，(3,1)，(3,2)，(3,4)．‎ 符合题意的基本事件有2个：(1,1)，(2,2)，‎ 故所求的概率P＝。‎ ‎【考点】等差、等比数列、古典概型。‎ ‎【解析】（I）根据已知求出公差和公比，即可求得an和bn、‎ ‎（II）根据概率的求法，找准两点：①全部等可能情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率。‎ 例17. （2012年陕西省文12分）假设甲乙两种品牌的同类产品在某地区市场上销售量相等，为了解他们的使用寿命，现从两种品牌的产品中分别随机抽取100个进行测试，结果统计如下：‎ ‎（Ⅰ）估计甲品牌产品寿命小于200小时的概率；‎ ‎（Ⅱ）这两种品牌产品中，，某个产品已使用了200小时，试估计该产品是甲品牌的概率 ‎【答案】解：（Ⅰ）甲品牌产品寿命小于200小时的频率为：，[来源:Zxxk.Com]‎ 用频率估计概率，得甲品牌产品寿命小于200小时的概率为：。‎ ‎（Ⅱ）根据抽样结果寿命大于200小时的产品有75+70=145个，其中甲品牌产品是75个，所以在样本中，寿命大于200小时的产品是甲品牌的频率是，‎ 用频率估计概率，得已使用了200小时的该产品是甲品牌的概率为：。‎ ‎【考点】用样本的频率分布估计总体分布，频率分布直方图。‎ ‎【解析】（Ⅰ）先从频数分布图中得到甲品牌产品寿命小于200小时的个数，与总数相比求出频率，即可得到概率。‎ ‎（Ⅱ）先求出已使用了200小时的产品总数，再找到是甲品牌的个数，二者相比即可得到结论。‎