2019年高考数学总复习检测第43讲　简单的线性规划问题 4页

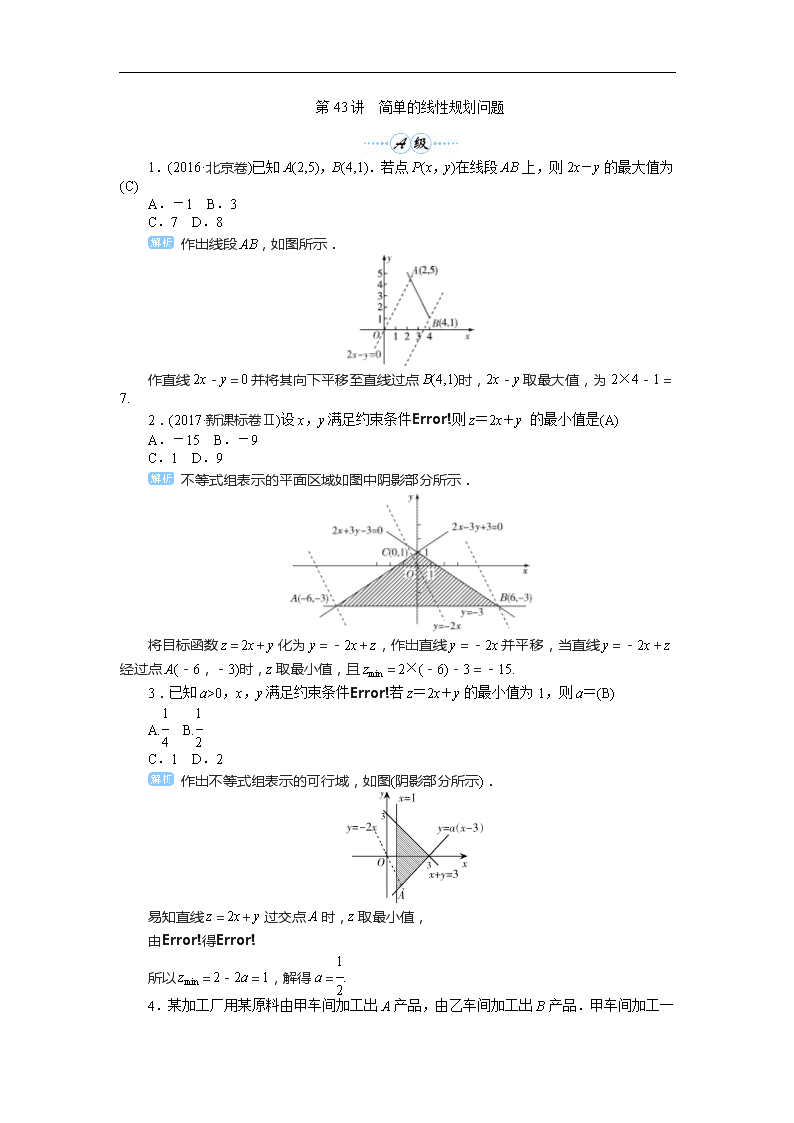
第43讲　简单的线性规划问题 ‎1．(2016·北京卷)已知A(2,5)，B(4,1)．若点P(x，y)在线段AB上，则2x－y的最大值为(C)‎ A．－1 B．3‎ C．7 D．8‎ ‎ 作出线段AB，如图所示．‎ 作直线2x－y＝0并将其向下平移至直线过点B(4,1)时，2x－y取最大值，为2×4－1＝7.‎ ‎2．(2017·新课标卷Ⅱ)设x，y满足约束条件则z＝2x＋y 的最小值是(A)‎ A．－15 B．－9‎ C．1 D．9‎ ‎ 不等式组表示的平面区域如图中阴影部分所示．‎ 将目标函数z＝2x＋y化为y＝－2x＋z，作出直线y＝－2x并平移，当直线y＝－2x＋z经过点A(－6，－3)时，z取最小值，且zmin＝2×(－6)－3＝－15.‎ ‎3．已知a>0，x，y满足约束条件若z＝2x＋y的最小值为1，则a＝(B)‎ A. B. C．1 D．2‎ ‎ 作出不等式组表示的可行域，如图(阴影部分所示)．‎ 易知直线z＝2x＋y过交点A时，z取最小值，‎ 由得 所以zmin＝2－2a＝1，解得a＝.‎ ‎4．某加工厂用某原料由甲车间加工出A产品，由乙车间加工出B产品．甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品，每千克A产品获利40元，乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品，每千克B产品获利50元．甲、乙两车间每天共能完成至多70箱原料的加工，每天甲、乙两车间耗费工时总和不得超过480小时，甲、乙两车间每天总获利最大的生产计划为(B)‎ A．甲车间加工原料10箱，乙车间加工原料60箱 B．甲车间加工原料15箱，乙车间加工原料55箱 C．甲车间加工原料18箱，乙车间加工原料50箱 D．甲车间加工原料40箱，乙车间加工原料30箱 ‎ 设甲车间加工x箱原料，乙车间加工y箱原料，甲、乙两车间每天总获利为z元．‎ 依题意，得z＝7×40x＋4×50y＝280x＋200y，画出可行域如图阴影部分，‎ 联立解得 知z在A点处取得最大值，故选B.‎ ‎5．(2015·新课标卷Ⅱ)若x，y满足约束条件则z＝2x＋y的最大值为　8　.‎ ‎ 画出可行域(如图所示)，通过平移直线y＝－2x分析最优解．‎ 因为z＝2x＋y，所以y＝－2x＋z，‎ 将直线y＝－2x向上平移，经过点B时z取得最大值．‎ 由解得 所以zmax＝2×3＋2＝8.‎ ‎6．若实数x，y满足则 ‎(1)的取值范围为　[2，＋∞)　；‎ ‎(2)x2＋y2的取值范围为　(1,5]　.‎ ‎　　 作出可行域，其可行域是顶点分别为A(0,1)，B(1,2)，C(0,2)的三角形及其内部(但不包括AC边)．‎ ‎(1)因为表示可行域内的点(x，y)与(0,0)连线的斜率，可知其取值范围为[2，＋∞)．‎ ‎(2)因为x2＋y2表示可行域内的点(x，y)到(0,0)的距离的平方，可知其取值范围为(1,5]．‎ ‎7．给定区域D：令点集T＝{(x0，y0)∈D|x0，y0∈Z，(x0，y0)是z＝x＋y在D上取得最大值或最小值的点}，问T中的点共确定多少条不同的直线？‎ ‎ 画出不等式组所表示的平面区域(如下图所示)．‎ 令z＝0，得直线l：x＋y＝0，平移直线l，由图象可知当直线经过整点A(0,1)时，z取最小值，当直线经过整点B(0,4)，C(1,3)，D(2,2)，E(3,1)，F(4,0)时，z取最大值．‎ 所以T＝{(0,1)，(0,4)，(1,3)，(2,2)，(3,1)，(4,0)}，‎ 所以T中的点可确定的直线有AB，AC，AD，AE，AF，BF共6条不同的直线．‎ ‎8．(2016·浙江卷)若平面区域夹在两条斜率为1的平行直线之间，则这两条平行直线间的距离的最小值是(B)‎ A. B. C. D. ‎ 根据约束条件作出可行域如图阴影部分，‎ 当斜率为1的直线分别过A点和B点时满足条件，‎ 联立方程组求得A(1,2)，‎ 联立方程组求得B(2,1)，‎ 可求得分别过A，B点且斜率为1的两条直线方程为x－y＋1＝0和x－y－1＝0，‎ 由两平行线间的距离公式得距离为＝，故选B.‎ ‎9．已知x，y满足约束条件当目标函数z＝ax＋by(a>0，b>0)在该约束条件下取到最小值2时，a2＋b2的最小值为　4　.‎ ‎ 不等式组表示的平面区域如图中阴影部分所示．‎ 由于a>0，b>0，所以目标函数z＝ax＋by在点(2,1)处取得最小值，即2a＋b＝2.‎ ‎(方法一)a2＋b2＝a2＋(2－2a)2＝5a2－8a＋20‎ ‎＝(a－4)2＋4≥4.‎ 即a2＋b2的最小值为4.‎ ‎(方法二)表示坐标原点与直线2a＋b＝2上的点之间的距离，故的最小值为 ＝2.‎ 即a2＋b2的最小值为4.‎ ‎10．(2017·天津卷)电视台播放甲、乙两套连续剧，每次播放连续剧时，需要播放广告．已知每次播放甲、乙两套连续剧时，连续剧播放时长、广告播放时长、收视人次如下表所示：,连续剧播放时长(分钟),广告播放时长(分钟),收视人次(万)甲,70,5,60乙,60,5,25已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟，广告的总播放时间不少于30分钟，且甲连续剧播放的次数不多于乙连续剧播放次数的2倍．分别用x，y表示每周计划播出的甲、乙两套连续剧的次数．‎ ‎(1)用x，y列出满足题目条件的数学关系式，并画出相应的平面区域；‎ ‎(2)问电视台每周播出甲、乙两套连续剧各多少次，才能使总收视人次最多？‎ ‎ (1)由已知，x，y满足的数学关系式为 即 该二元一次不等式组所表示的平面区域为图①中的阴影部分中的整数点．‎ ‎①‎ ‎②‎ ‎(2)设总收视人次为z万，则目标函数为z＝60x＋25y.‎ 考虑z＝60x＋25y，将它变形为y＝－x＋，这是斜率为－，随z变化的一组平行直线.为直线在y轴上的截距，当取得最大值时，z的值就最大．‎ 又因为x，y满足约束条件，所以由图②可知，当直线z＝60x＋25y经过可行域上的点M时，截距最大，即z最大．‎ 解方程组得则点M的坐标为(6,3)．‎ 所以，电视台每周播出甲连续剧6次、乙连续剧3次时，才能使总收视人次最多．‎